Electric Displacement | Electricity & Magnetism - Physics PDF Download
Gauss Law in the Presence of Dielectrics
Within the dielectric, the total charge density can be written as ρ = ρb +ρf where ρb is volume bound charge ρf free charge density.
From Gauss Law,
where 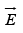 is now the total field, not just that portion generated by polarization.
is now the total field, not just that portion generated by polarization.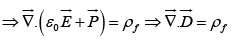
where 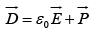 is known as the electric displacement.
is known as the electric displacement.
Thus Gauss’ law reads,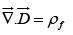
or, in integral form 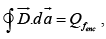 where
where 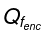 denotes the total free charge enclosed in the volume.
denotes the total free charge enclosed in the volume.
Linear Dielectrics (Susceptibility, Permittivity, Dielectric Constant)
For any substances, the polarization is proportional to the field provided 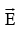 is not too strong:
is not too strong: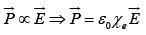
(Materials that obey this relation are called linear dielectrics)
The constant of proportionality, 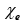 is called the electric susceptibility of the medium. The value of
is called the electric susceptibility of the medium. The value of 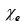 depends on the microscopic structure of the substance and also on external conditions such as temperature.
depends on the microscopic structure of the substance and also on external conditions such as temperature.
In linear media we have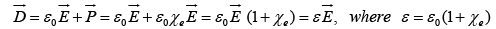
This new constant ε is called the permittivity of the material.
Also, 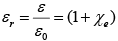 is called relative permittivity or dielectric constant, of the material.
is called relative permittivity or dielectric constant, of the material.
Boundary Condition on 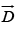
The boundary between two medium is a thin sheet of free surface charge σf . The Gauss's law states that 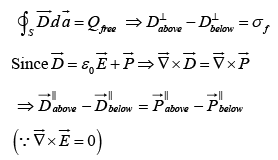
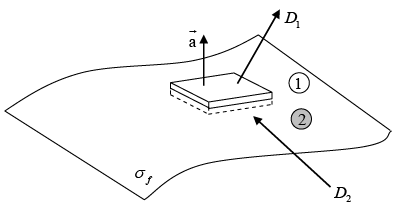
Energy in dielectric system
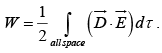
Example 30: A metal sphere of radius a carries a charge Q . It is surrounded, out to radius b , by linear dielectric material of permittivity ε . Find the potential at the center.
for all points r >a
(Inside the metal sphere,) Once we know
, it is a trivial matter to obtain
Potential at the center is therefore
Image Problems
The Classic Image Problem
Suppose a point charge q is held a distance d above an infinite grounded conducting plane. We can find out what is the potential in the region above the plane.
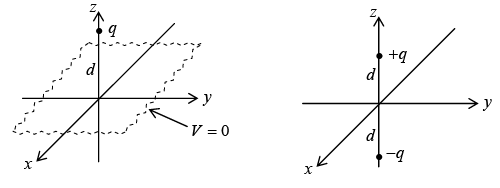
Forget about the actual problem; we are going to study a complete different situation. The new problem consists of two point charges +q at ( 0, 0, d ) and −q at ( 0, 0, − d) and no conducting plane. For this configuration we can easily write down the potential: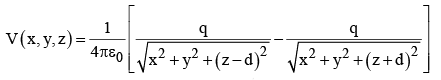
(The denominators represent the distances from ( x, y, z ) to the charges + q and −q , respectively.) It follows that
1. V = 0 when z = 0 and
2. V → 0 for x2 + y2 +z2 >> d2,
and the only charge in the region z > 0 is the point charge + q at ( 0, 0, d ) . Thus the second configuration produces exactly the same potential as the first configuration, in the upper region z ≥ 0.
Induced Surface Charge
The surface charge density σ induced on the conductor surface can be calculated by 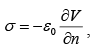
where 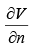 is the normal derivative of V at the surface. In this case the normal direction is the z -direction, so
is the normal derivative of V at the surface. In this case the normal direction is the z -direction, so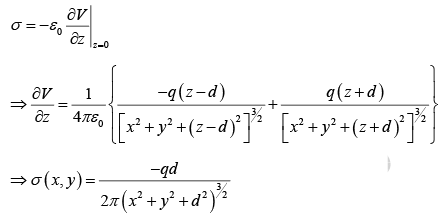
As expected, the induced charge is negative (assuming q is positive) and greatest at x =y= 0.
The total induced charge 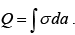
This integral, over the xy -plane, could be done in Cartesian coordinates, with da = dx dy , but its easier to use polar coordinates (r ,φ) , with r2 =x2 + y2 and da = rdrdφ.
Then
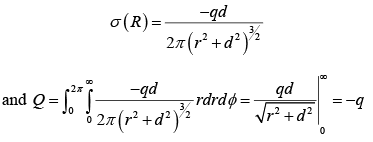
Force and Energy
The charge q is attracted towards the plane, because of the negative induced surface charge. The force: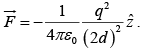
One can determine the energy by calculating the work required to bring q in from infinity.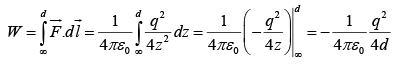
Example 31: Find the force on the charge + q as shown in figure (The xy – plane is a grounded conductor).
Place image charges +2q at z =−d and −q at z = −3d . Total force on +q is
Other Image Problem
The method just described is not limited to a single point charge; any stationary charge distribution near a grounded conducting plane can be treated in the same way, by introducing its mirror image.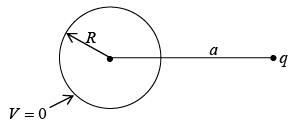
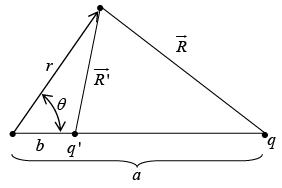
Let us examine the completely different configuration, consisting of the point charge q together with another point charge
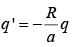
placed at a distance
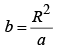
to the right of the centre of sphere. No conductor, now-just two point charges. The potential of this configuration is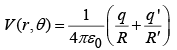
where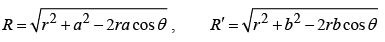

Clearly when r =R, V→ 0
Induced charge
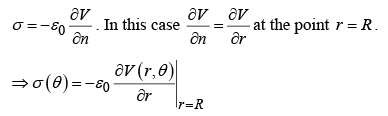
But a > R (else q would be inside), so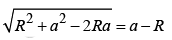
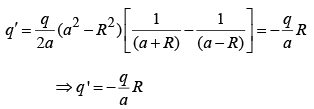
Force
The force on q, due to the sphere, is the same as the force of the image charge q′, thus:
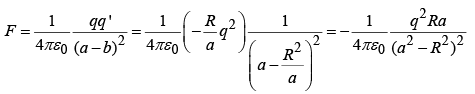
Energy
To bring q in from infinity to a, we do work
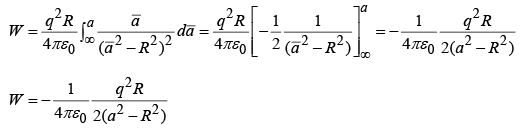
|
82 videos|29 docs|22 tests
|
FAQs on Electric Displacement - Electricity & Magnetism - Physics
| 1. What is electric displacement in the context of IIT JAM? |  |
| 2. How is electric displacement related to the IIT JAM exam? |  |
| 3. What is the formula for electric displacement? |  |
| 4. How is electric displacement different from electric field? |  |
| 5. What are some applications of electric displacement in real-life scenarios? |  |

|
Explore Courses for Physics exam
|

|
 for all points r >a
for all points r >a ) Once we know
) Once we know  , it is a trivial matter to obtain
, it is a trivial matter to obtain 





















