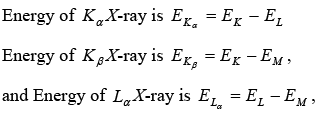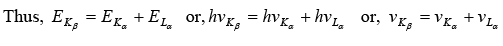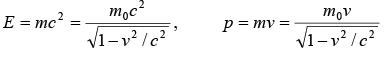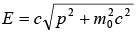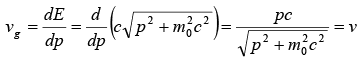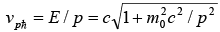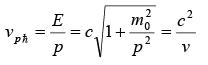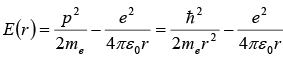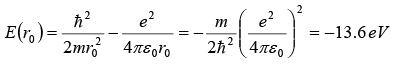Bohr Atomic Model | Modern Physics PDF Download
Introduction
In atomic physics, the Bohr model, introduced by Niles Bohr in 1913, depicts the atom as small, with a positively charged nucleus surrounded by electrons that travel in circular orbits around the nucleus-similar in structure to the solar system, but with attraction provided by electrostatic forces rather than gravity. He suggested that electrons could only have certain classical motions:
1. Electrons in atoms orbit the nucleus.
2. The electrons can only orbit stably, without radiating, in certain orbits (called by Bohr the "stationary orbits"): at a certain discrete set of distances from the nucleus. These orbits are associated with definite energies and are also called energy shells or energy levels. In these orbits, the electron's acceleration does not result in radiation and energy loss as required by classical electromagnetic.
3. Electrons can only gain and lose energy by jumping from one allowed orbit to another, absorbing or emitting electromagnetic radiation with a frequency ν determined by the energy difference of the levels according to the Planck relation:
ΔE = E2 - E1 = hv
where h is Planck’s constant . The frequency of the radiation emitted at an orbit of period T is as it would be in classical mechanics; it is the reciprocal of the classical orbit period: v = 1/T
Bohr Quantization Rule
The significance of the Bohr model is that the laws of classical mechanics apply to the motion of the electron about the nucleus only when restricted by a quantum rule. The angular momentum L is restricted to be an integer multiple of a fixed unit:
L = nℏ where n = 1, 2, 3... and
n is called the principle quantum number , and ℏ = h/2π. The lowest value of n is 1this gives a smallest possible orbital radius of 0.592A0 known as the Bohr radius.
Hydrogen Atom
A hydrogen atom is an atom of the chemical element hydrogen. The electrically neutral atom contains a single positively charged proton and a single negatively charged electron bound to the nucleus by the Coulomb force. According to Bohr electron revolve about the nucleus in different quantized circular orbits whose angular momentum is given by L = nℏ where n = 1, 2, 3... .The electron is held in a circular orbit by electrostatic attraction. The centripetal force is equal to the Coulomb force.
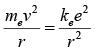
where me is the electron's mass, e is the charge of the electron, ke = 1/4πεo is Coulomb's constant and v is velocity of electrons in orbit.
This equation determines the electron's speed at any radius: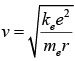
It also determines the electron's total energy at any radius: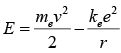
Putting the value of v one will get
The total energy is negative and inversely proportional to r. This means that it takes energy to pull the orbiting electron away from the proton. For infinite values of r, the energy is zero, corresponding to a motionless electron infinitely far from the proton. The total energy is half the potential energy,
From the quantization the angular momentum
L = nℏ = mevr = nℏ
Substituting the expression for the velocity gives an equation for r in terms of n :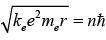
So that the allowed orbit radius at any n is: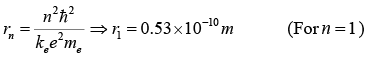
The smallest possible value of r in the hydrogen atom is called the Bohr radius r1. The energy of the nth level for any atom is determined by the radius and quantum number: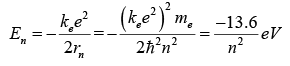
The combination of natural constants in the energy formula is called the Rydberg energy
RE which is given by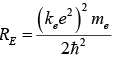
This expression is clarified by interpreting it in combinations which form more natural units: mec2 is the rest mass energy of the electron (511 keV).
kee2/ℏc = α = 1/137 is the fine structure constant.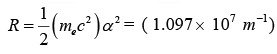
For nuclei with Z protons, the energy levels are (to a rough approximation):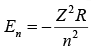
The Structure and Spectra of Hydrogenic Atoms
Atomic Spectra
The spectrum of atomic hydrogen arises from transitions between its permitted states.
- Each element has a characteristic line spectrum
- When an atomic gas is excited by passing electric current, it emits radiation. The radiation has a spectrum which contains certain specific wavelength, called Emission line spectrum.
- When while light is passed through a gas, gas absorb light of certain wavelength present in its emission spectrum. Resulting spectrum is called Absorption line spectrum.
- The number, intensity and exact wavelength of the lines in the spectrum depend on Temperature, Pressure, Presence of Electric field, Magnetic field, and the motion of the source.
Spectral series
When an electric discharge is passed through gaseous hydrogen, the H2 molecules dissociate and the energetically excited H atoms that are produced emit light of discrete frequencies, producing a spectrum of a series of 'lines'.
(i) Lyman Series: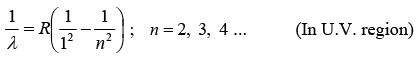
Where, R is Rydberg constant ( 1.097x 107 m-1)
(ii) Balmer Series:
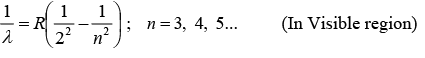
n = 3 for Hα Line. n = 4 for Hβ Line, n = 5 for Hγ. Line,
(iii) Paschen series: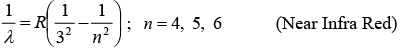
(iv) Bracket Series:

(v) Pfund Series: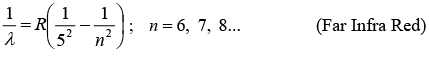
If mass of nucleus is not considered as very heavy then reduce mass will take in to account which is given by 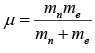 where me and mn are mass of electron and nucleus respectively.
where me and mn are mass of electron and nucleus respectively.
- Correction in Energy due to Reduced Mass
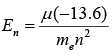
- Correction in Rradius of the orbit
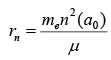
- Variation of Rydberg constant with respect to Atomic Mass
R for infinitely heavy nucleus: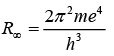
R for nucleus of mass M: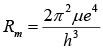
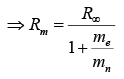

- Spectral Wavelength for Hydrogen like atoms
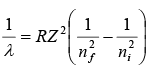 where R is Red berg and Z is atomic number.
where R is Red berg and Z is atomic number.
X-radiation (composed of X-rays) is a form of electromagnetic radiation. X-rays have a wavelength in the range of 0.01 to 10 nanometers, corresponding to frequencies in the range (3 × 1016 Hz to 3 × 1019 Hz) and energies in the range 100 eV to 100 keV. The wavelengths are shorter than those of UV rays and longer than of gamma rays.
When the electrons hit the target, X-rays are created by two different atomic processes:
- X-ray fluorescence: If the electron has enough energy it can knock an orbital electron out of the inner electron shell of a metal atom, and as a result electrons from higher energy levels then fill up the vacancy and X-ray photons are emitted. This process produces an emission spectrum of X-rays at a few discrete frequencies, sometimes referred to as the spectral lines. The spectral lines generated depend on the target element used and thus are called characteristic lines. Usually these are transitions from upper shells into K shell (called K lines), into L shell (called L lines) and so on.
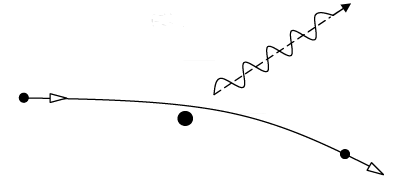
- Bremsstrahlung (breaking radiation): electromagnetic theory predicts that an accelerated electric charge will radiate electromagnetic waves, and a rapidly moving electron suddenly brought to rest is certainly accelerated.
 X- ray spectra of tungsten and molybdenum at 35KV accelerating potential.
X- ray spectra of tungsten and molybdenum at 35KV accelerating potential.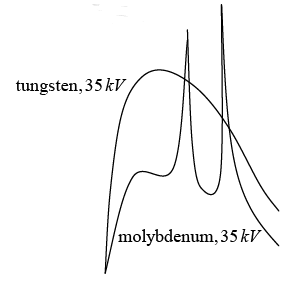
Analysis:
An electron of initial kinetic energy K is decelerated during an encounter with heavy target nucleus .the electron interacts with the charge nucleus via the coulomb field , transferring momentum to the nucleus . the accompanying deceleration of the electron lead to photon emission . the target nucleus is so massive that the energy it acquires during the collision can safely be neglected.
If K' is the kinetic energy of the electron after the electron then energy of photon is given by hv = K - K' and photon (X- ray) wavelength is given by hc/λ = K - K'
The shortest wavelength photon would be emitted when an electron loses all the kinetic energy in one deceleration process so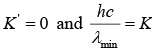
Since K = eV the energy acquired by the electron in being accelerated through the potential difference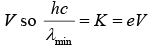
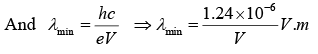
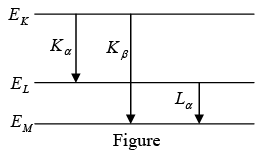
Example 9: Show that the frequency of KβX-ray of a material equals the sum of the frequencies of Kα and Lα X-rays of the same material.
The energy level diagram of an atom with one electron knocked out is shown in figure.
Wave Particle Duality
Wave-Particle Duality: Postulates that all particles exhibit both wave and particle properties. A central concept of quantum mechanics, this duality addresses the inability of classical concepts like "particle" and "wave" to fully describe the behavior of quantum-scale object.
List of experiments which explain particle nature of light wave.
Photoelectric effect
Compton Effect
Pair production
List of experiments which explain wave nature of particle
Davisson –Germen effect (diffraction due to electrons)
Young double slit Interference due to electrons
De Broglie Wave
In quantum mechanics, the concept of matter waves or de Broglie waves reflects the wave–particle duality of matterThe de Broglie relations show that the wavelength is inversely proportional to the momentum of a particle and is also called de Broglie wavelength.
The wavelength of the wave associated with a particle as given by the de Broglie relation
λ = h/p = h/mv
For relativistic case, the mass becomes 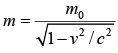 where m0 is rest mass and v is velocity of body.
where m0 is rest mass and v is velocity of body.
Uncertainty Principle
“It is impossible to determine two canonical variable simultaneously for microscopic particle”. If q and pq are two canonical variable then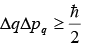
where, Δq is the error in measurement at q and Δpq is error in measurement at pq and h is Planck’s constant (ℏ ≡ h/ 2π).
Important uncertainty relations:
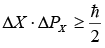 (X is position and px is momentum in x direction)
(X is position and px is momentum in x direction) 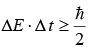 (E is energy and t is time).
(E is energy and t is time).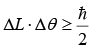 (L is angular momentum, θ is angle measured)
(L is angular momentum, θ is angle measured)
Superposition Principle
According to de Broglie, matter waves are associated with every moving body. These matter waves moves in a group of different waves having slightly different wavelength. The formation of group is due to superposition of individual wave.
Analogy: If ψ1(x,t) and ψ2(x,t) are two waves of slightly different wavelength an frequency.
ψ1 - A sin(kx - ωt)
ψ2 = A sin[(k + dk)x - (ω + dω)t]
ψ = ψ1 + ψ2
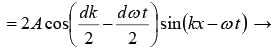 The velocity of individual wave is known as Phase velocity which is given as vp = ω/k
The velocity of individual wave is known as Phase velocity which is given as vp = ω/k
The velocity of amplitude is given by group velocity vg which is given by dω/dk.
vg = dω/dk
The relationship between group and phase velocity is given by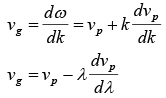
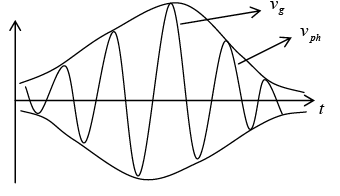
Due to the superposition of different wave of slightly different wavelength resultant wave moves like a wave packet with a velocity equal to group velocity.
Example 10: Calculate the group and phase velocities for the wave packet corresponding to a relativistic particle.
Recall that the energy and momentum of ta relativistic particle are given by
where m0 is the rest mass of the particle and c is the speed of light in a vacuum. Squaring and adding the expressions of E and p, we obtain E2 = p2c2 + m20 c4, hence
Using this relation along with P2 + m20c2 / (1 - v2 / c2) and , we can show that the groupvelocity is given as follows
The group velocity is thus equal to the speed of the particle,
vg = v
The phase velocity can be found from and:
which, when combined with
hence
Example 11: Use the uncertainty principle to estimate:
(a) the ground state radius of the hydrogen atom
(b) the ground state energy of the hydrogen atom
(a) According to the uncertainty principle, the electron’s momentum and the radius of its orbit are related by rp ~ ℏ , hence p ~ ℏ / r. To find the ground state radius, we simply need to minimize the electron-proton energy
with respect to r :
This leads to the Bohr radius
(b) Inserting we obtain the Bohr energy;
The results obtained for r0 and E(r0), as shown in, are indeed impressively accurate given the crudeness of the approximation.
|
37 videos|17 docs|19 tests
|
FAQs on Bohr Atomic Model - Modern Physics
| 1. What is wave-particle duality? |  |
| 2. What is the Bohr atomic model? |  |
| 3. How does wave-particle duality relate to the Bohr atomic model? |  |
| 4. What experimental evidence supports wave-particle duality? |  |
| 5. How does the Bohr atomic model explain the emission and absorption spectra of atoms? |  |