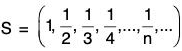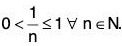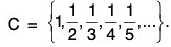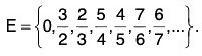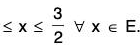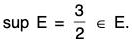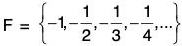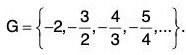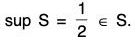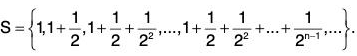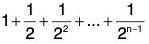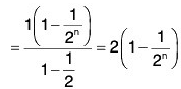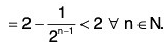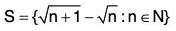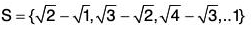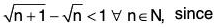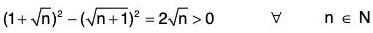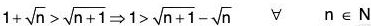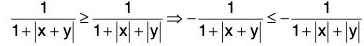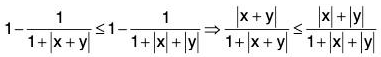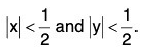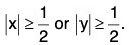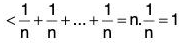Point Set Topology - I | Mathematics for Competitive Exams PDF Download
| Table of contents |

|
| Sets |

|
| Set Theoretic Concepts |

|
| Function or Mapping |

|
| Real Numbers |

|
| Bounded Set |

|
| Completeness Of R |

|
| Complete Ordered Field |

|
| Absolute Value of Modulus of a Real Number |

|
Sets
A set is a well defined collection of objects. The objects of the set are called elements or members of set of Capital letters X, Y, S, T etc. generally denote sets, while small letters x, y, s, t etc. denote elements of a set. If x is an element of set S, then we write x ∈ S and read it as ‘x belongs to S’ or ‘x is a member o f S’. If x is not an element o f a set S, then
we write x « S and read it as ‘x does not belong to S’ or 'x is not a member of S’.
A set having no element is called an empty set or a null set. It is denoted by Ф or { }.
A non-empty set S, written as S ≠ Ф, is a set which has at least one element. S = {1}
A set is said to be finite or infinite according to the number of elements present in the set.
Examples
1. N = {1, 2, 3, 4, ...} is the set of natural numbers.
Here 0 ∉ N.
2. I = { ..., - 3 , - 2 , - 1 , 0, 1, 2, 3, ...} is the set o f integers.
3. The set S = {11, 12, 13, 14, ...} may be written as S = {x : x ∈ N and x > 10}.
4. The set T = {..., -15, -10, -5, 0, 5, 10, 15......} may be written as T = {5x : x ∈ I}.
5. The set S = {x : x ∈ N and 2 < x < 3} is an empty set i.e., S = Ф.
Set Theoretic Concepts
Definition 1 : If S and T be two sets such that every element of S is also an element of T, then we say that S is a subset of T or S is contained in T.
Symbolically, S ⊂ T , if x ∈ S ⇒ x ∈ T ∀ x ∈ S .
If S is contained in T, then we also say that T contains S or T is a super set of S and write
it as T ⊃ S.
Thus S ⊂ T ⇔ T ⊃ S.
Example
1. Let S = {1, 3, 5} and T = {1, 2, 3, 4, 5}. Then S ⊂ T .
2. Let S = {1, 3, 6} and T = {1, 2, 3, 4, 5}.
Then S ⊂ T, since 6 e S but 6 ∉ T.
Note: The empty set Ф is a subset of every set,
Definition 2 : Two sets S and T are said to be equal, written as S = T, if and only if S ⊂ T and T ⊂ S. Or we can say that two sets are said to be equal if they contain the same elements.
Example
{2, 3, 5, 7} = {7, 2, 5, 3} and {2, 3, 5, 7} ≠ {2, 5, 7, 6}.
Definition 3 : The union of two sets S and T, denoted as S ∪ T, is defined as
S ∪ T = {x : x ∈ S or x ∈ T}.
In other words, S ∪ T contains all the elements of S as well as T.
Definition 4 : The intersection of two sets S and T, denoted as S ∩ T, is defined as
S ∩ T = { x : x ∈ S and x ∈ T}.
In other words, S ∩ T contains the common elements of S and T.
Definition 5 : Two sets S and T are said to be disjoint if S ∩ T = Φ.
Examples
1. Let S = {1, 3, 5}, T = {2, 3, 4, 5, 7}
Then S ∪ T = {1, 2, 3, 4, 5, 7} and S ∩ T = {3, 5}.
2. Let E = -6, -4, -2, 0, 2, 4, 6, ...},
O = {... - 5 , - 3 , - 1 , 1, 3, 5, ...}.
Then E ∪ O = I (set of all integers)
and E ∩ O = Ф. Thus E and O are disjoint sets.
Note :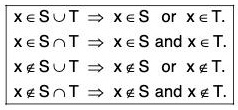
Definition 6. A non-empty set Δ is said to be an index set for the family S = {Sλ} of sets if for each λ ∈ Δ, there exists a set Sλ in the family S.
For Example, N = {1, 2, 3, 4, .......} is an index set for the family of sets {S1, S2, S3, S4, ...}.
Consider an arbitrary family of sets {Sλ: λ ∈ Δ}, Δ is any index set.
Definition 7. The union of the sets {Sλ} is defined as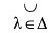 Sλ = {x : x ∈ Sλ for some λ ∈ Δ}.
Sλ = {x : x ∈ Sλ for some λ ∈ Δ}.
Definition 8. The intersection of the sets {Sλ} is defined as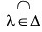 Sλ {x : x ∈ Sλ for each λ ∈ Δ}.
Sλ {x : x ∈ Sλ for each λ ∈ Δ}.
Definition 9. If S and T are two sets, then the difference of S and T, denoted as S ~ T, is defined as
S ~ T = { x : x ∈ S and x ∉ T}.
For Example, if S = {1, 2, 3, 4, 8} and T = {2, 3, 5, 6, 7}, then
S ~ T = {1, 4, 8}.
Definition 10. If S is a subset of a set X, then the complement of S, denoted by X ~ S, is defined as
X ~ S = { x : x ∈ X and x ∉ S}.
Other notations of the complement of S and S’ or Sc.
Thus x ∈ X ~ S ⇒ x ∈ X but x ∉ S.
For Example, if X = {1, 2, 3, 4, ..., 10}, and S = {2, 4, 6, 8, 10}, then X ~ S = {1, 3, 5, 7, 6}.
Remarks
- S ∪ S = S, S ∩ S = S.
- S ∪ T = T ∪ S, S ∩ T = T ∩ S.
- Su Ф = S, S V Ф = Ф.
- Sλ ⊂
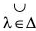 Sλ for each λ ∈ Δ.
Sλ for each λ ∈ Δ. 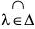 Sλ ⊂ Sλ for each X ∈ Δ.
Sλ ⊂ Sλ for each X ∈ Δ.- A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C).
- A ∪ (B ∩ C) = (A ∪ B) n (A ∪ C).
- (De Morgan’s Laws)
If S and T be any two subsets of a set X, then
(i) X ~ (S ∪ T) = (X ~ S) n (X ~ T).
(ii) X ~ (S ∩ T) = (X ~ S) u (X ~ T).
Proof. We recall that
A = B ⇔ A ⊂ B and B ⊂ A .
(i) We see that x ∈ X ~ (S ∪ T)
⇔ x ∈ X but ∉ S ∪ T
⇔ x ∈ X but x ∉ S and x ∉ T
⇔ x ∈ X ~ S and x ∈ X ~ T
⇔ x ∈ (X ~ S) ∩ (X ~ T),
Hence X ~ (S ∪ T) = (X ~ S) ∩ (X ~ T).
(ii) Now x ∈ X ~ (S ∩ T)
⇔ X ∈ X but X 5 ∉ S ∪ T
⇔ X ∈ X but X ∉ S or X ∉ T
⇔ X ∈ X ~ S o r x ∈ X ~ T
⇔ x ∈ (X ~ S) ∪ (X ~ T).
Hence X ~ (S ∩ T) = (X ~ S) ∪ (X ~ T).
- The above laws can be generalised as follow :
(i)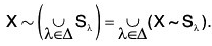
(ii)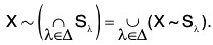
(Here each Sλ is a subset of X).
Function or Mapping
Definition 1 : If S and T are two non-empty sets, then a function from S to T is a rule, denoted as
F : S → T
which associates to each element x ∈ S a unique element y ∈ T.
The element y, written as y = f(x), is called the image of x and x is called a pre-image of y.
The set S is called the domain and T the co-domain of the function f : S → T.
The set f(S) = {f(x) : x ∈ S} is called the range of the function f : S → T. f : N → N defined by f(n) = n2 is a function whose range is {1, 4, 9, 16, 25,
Definition 2 : A mapping f : S → T is called one-to-one, if
x ≠ y ⇒ f(x) ≠ f(y) ∀ x, y ∈ S.
Or f(x) = f(y) ⇒ x = y ∀ x, y ∈ S.
Definition 3 : A mapping f : S → T is called onto, if for each t ∈ T, there exists some s ∈ S such that f(s) = t.
Definition 4 : Two mappings f : S → T and g : S → T are said to be equal,
if f(x) = g(x) ∀ x ∈ S.
Definition 5 : The product or the composition of two mappings
f : S → T and g : T → U
is defined as the mapping
gof : S → U
such that (gof) (x) = g(f(x)) ∀ x ∈ S .
Examples
1. f : N → N defined as f(x) = x2 v x ∈ N is one-to-one,
since for any x, y ∈ N,
x ≠ y ⇒ x2 ≠ y2 ⇒ f(x) ≠ f(y).
However, f is not onto ; since for 2 ∈ N, there does not exist any x ∈ N such that f(x) = 2. (Notice that x2 = 2 ⇒ x = ± √2 ∈ N)
2. f : I → I defined as f(x) = x + 3 ∀ x ∈ l is one-to-one and onto.
Let x, y ∈ I then f(x) = f(y) ⇒ x + 3 = y + 3 ⇒ x = y s o f i s one-to-one. Let x e I be arbitrary. Then y = x - 3 ∈ I and f(y) = x - 3 + 3 = x and so f is onto.
3. f : I → I defined by f(x) = x2 ∀ x ∈ I, is not one-to-one.
Notice that 2 ⇒ -2 but f(2) = f(-2) = 4. Also f is not onto.
4. Let f : N → N and g : N → N be defined as
f(x) = 2x + 3 and g(x) = x2 ∀ x ∈ N.
Then gof : N → N is given by
(gof) (x) = g (f(x)) = g (2x + 3) = (2x + 3)2.
Also fog : N → N is given by
(fog) (x) = f(g(x)) = f(x2) = 2x2 + 3.
In general, fog ≠ gof.
Real Numbers
We are familiar with the following sets of numbers :
N = {1, 2, 3 , ..... } is the set of natural numbers.
Z = { ...... - 3 , - 2 , - 1 , 0, 1, 2, 3 , ....... } is the set of integers
The other notations of the set of integer are I or J.
Q = {p/q : and q are integers and q ≠ 0} is the set of rational numbers. Thus a rational numbers is of the form p/q, where p and q are integers and q ≠ 0.
It is clear that N ⊂ Z ⊂ Q (e.g., 3 = 3/1, 0 = 0/1, - 4 = -4 /1 ).
It may be noted that any rational number x ∈ Q can be expressed as x = p/q, where p and q are co-prime integers i.e., the H.C.F. of p and q is 1, denoted as (p, q) = 1.
For Example, 6/8 = 3/4, 9/15 = 3/5 etc.
There exist numbers which are not expressible as p/q, where p and q are integers and q ≠ 0, such numbers are called irrational numbers.
The set consisting of all rational and irrational numbers is called the set of real number, denoted by R. Thus x ∈ R ⇔ x is either a rational number or x is an irrational number.
We have N ⊂ Z ⊂ Q ⊂ R.
Example 1: Prove that √3 is not a rational number.
Let, if possible, √3 be a rational number.
Then √3 = p/q where p and q are integers and q ≠ 0.
We can further suppose that H.C.F. of p and q is 1.
Now 73 = p/q ⇒ p2 = 3q2. ...(1)
Since q ∈ I, so 3q2 ∈ I and 3 is a factor of 3q2.
By (1), 3 is a factor of p2 ⇒ 3 is a factor or p
⇒ p = 3m, for some m ∈ I.Putting p = 3m in (1), we get q2 = 3m2.
We have seen that p2 = 3q2 ⇒ 3 is a factor of p.
Similarly, q2 = 3m2 ⇒ 3 is a factor of q.
Thus, 3 is a common factor of p and q, which is a contradiction to the fact that H.C.F. of p and q is 1. Hence √3 must be an irrational number.
Example 2: Prove that √8 is not a rational number.
Let, if possible, √8 be a rational number.
Then √8 = p/q ; where p, q ∈ I, q > 0.
We can further suppose that H.C.F. of p and q is 1.
p
Clearly 2 < √8 < 3 ⇒ 2 < p/q < 3 ⇒ 2q < p < 3q ⇒ 0 < p - 2q < q
⇒ p - 2q is a positive integer less than q.
∴ √8 (p - 2q) is not an integer. ...(1)
Again > √8(p - 2q) = p/q(p-2q)= p2/q - 2p = p2/q2.q - 2p = 8q-2p
where 8q - 2p is an integer.
Thus √8 (P - 2q) is an integer. ...(2)
(1) and (2) are contradictory statements. Hence √8 is not a rational number.
Example 3: Prove that there is no rational number whose cube is 2.
Let, if possible, x3 = 2 ; x ∈ Q.
We may take x = p/q, where p and q are co-prime integers i.e., the H.C.F. of p and q is 1. We have x3 = 2 ⇒ p3 = 2q3 ⇒ p3 is a multiple of 2 and so p must be a multiple of 2, otherwise p3 will not a multiple of 2.
Let p = 2r, for some r e Z. Putting p = 2r in p3 = 2q3, we get q3 = 4r3 ⇒ q3 is a multiple of 2 and so q must be a multiple of 2. Since p and q are both multiples of 2, it follows that 2 divides p and q, which contradicts the fact that p and q are co-prime. Hence our assumption is wrong and so there is no rational number whose cube is 2.
Bounded Set
Definition 1 : A real number K is called an upper bound of a set S, if every element of S is
less than or equal to K
i.e. x < K ∀ x ∈ S.
If a set S has an upper bound, then the set S is called bounded above.
Definition 2 : A real number k is called a lower bound of a set S, if every element of S is greater than or equal to k.
i.e. k < x ∀ x ∈ S.
If a set S has a lower bound, then the set S is called bounded below.
Definition 3 : A set S is called bounded if it is both bounded above and bounded below. or
A set S is called bounded if ∃ two real numbers k and K such that
k < x < K ∀ x ∈ S .
Examples
1. The set S = {1, 2, 3, ..., 10} is bounded, 1 being a lower bound and 10 being an upper bound. Indeed 1 < x < 10 ∀ x ∈ S .
2. The set N = {1, 2, 3, ...} of natural numbers is bounded below but not bounded above, 1 being a lower bound. So N is not bounded.
3. The set S = {..., - 3 , - 2 , - 1 } is bounded above but not bounded below, -1 being an upper bound. So S is not bounded.
4. The set Z of integers is neither bounded above nor bounded below. So Z is not bounded. Similarly, the sets Q, R are not bounded.
Remarks
1. A set may or may not possess upper and/or lower bounds, e.g., N has a lower bound but has no upper bound.
2. Bounds of a set may or may not belong to the set.
If 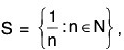 , its lower bound 0 ∉ S and upper bound 1 ∈ S.
, its lower bound 0 ∉ S and upper bound 1 ∈ S.
3. If a real number K is not an upper bound of a set S, then there exists at least one element y ∈ S such that y > K.
4. If a real number k is not a lower bound of a set S, then there exists at least one element z ∈ S such that k > z i.e., z < k.
5. If a set has one upper bound, then it has an infinite number of upper bounds.
Notice that if K is an upper bound of a set S, then any number K, (> K) is also an upper bound of S.
6. If a set has one lower bound, then it has an infinite number of lower bounds.
Notice that if k is a lower bound of a set S, then any number k, (< k) is also a lower bound of S.
Remarks 5 and 6 lead to the following :
Definition 4 : The smallest of all the upper bounds of a set S is called the supremum of the set S or the least upper bound (l.u.b.) of the set S.
Definition 5 : The greatest of all the lower bounds of a set S is called the infimum of the set S or the greatest lower bound (g.I.b.) of the set S.
Notation : If M and m are the supremum and infimum of a set S respectively, we write
m = inf S and M = sup S.
m and M are called the bounds of the set S, provided they exist.
Remarks
1. A set may or may not have the supremum or/and infimum.
2. The supremum and infimum of a set may or not belong to the set.
Example
1. If S = {1, 2, 3, ..., 10}, then inf S = 1 ∈ S, sup S = 10 ∈ S.
2. If S = 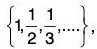 then inf S = 0 ∉ S, sup S = 1 ∈ S.
then inf S = 0 ∉ S, sup S = 1 ∈ S.
3. If S =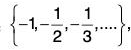 inf S = - 1 g S, sup S = 0 ∉ S.
inf S = - 1 g S, sup S = 0 ∉ S.
4. If S = 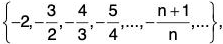 then inf S = - 2 ∈ S and sup S = - 1 ∉ S.
then inf S = - 2 ∈ S and sup S = - 1 ∉ S.
5. If S =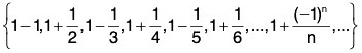 then inf S = 0 ∈ S, sup S =3/2 ∈ S.
then inf S = 0 ∈ S, sup S =3/2 ∈ S.
6. The set Z of integers has neither infimum nor supremum.
Example 4: Give an example of a set S which is
(i) bounded above but not bounded below,
(ii) bounded below but not bounded above,
(iii) neither bounded above nor bounded below,
(iv) bounded.
(i) s = { ...,- 3 , - 2 , - 1 }
is bounded above by - 1, but not bounded below.
(ii) N ={1, 2, 3, ...}
is bounded below by 1, but not bounded above.
(iii) I = {..., -3 , - 2 , - 1 , 0. 1.2 ,3 ,. ..} is neither bounded above nor bounded below.
(iv)
is bounded, since
Example 5: Give an Example of a non-empty bounded subset S of R whose supremum and infimum both belong to R ~ S.
Let S = {x : 0 < x < 1}. Then sup S = 1 ∈ R ~ S and inf S = 0 ∈ R ~ S.
Example 6: Which of the following sets are bounded above, bounded below, bounded or otherwise:
(i) A = {3, 32, 33,...,3n,...},
(ii) 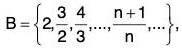
(iii) 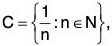
(iv) D = {-1, 2, -3, 4 .... ( 1 )n n,.....},
(v) 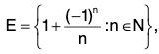
(vi) 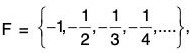
(vii)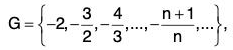
(viii) 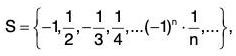
(ix) 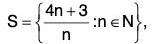
(x) 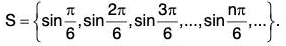
Find the supremum and infimum of the above sets, if they exist.
(i) A is bounded below by 3, but is not bounded above inf A = 3 ∈ A but sup A does not exist,
(ii) B is bounded, as 1 < x < 2 ∀ x ∈ B.inf B = 1 ∉ B, sup B = 2 ∈ B.
(iii)
C is bounded, as 0 < x < 1 ∀ x ∈ C.
inf C = 0 ∉ C, sup C = 1 ∈ C.
(iv) D is neither bounded above nor bounded below.
(v)
E is bounded, as 0
inf E = 0 ∈ E,
(vi)
F is bounded, since -1 < x < - 0 ∀ x ∈ F.
inf F = -1 ∈ F, sup F = - 0 ∈ F.
(vii)
G is bounded, since -2 < x < -1 ∀ x ∈ G.
inf G = -2 ∈ G. sup G = -1 ∉ G.
(viii)is bounded.
inf S = -1 ∈ S.
(ix)is bounded.
sup S = 7 ∈ S, inf S = 4 ∉ S.
(x)is bounded.
sup T = 1 ∈ T, inf T = -1 ∈ T.
Example 7: Find the supremum and infimum of the set :
We have
Hence sup S = 2, inf S = 1.
Example 8: The supremum of a non-empty set S, if it exists, is always unique.
Let, if possible, k, k’ be two suprema of S.
Now k’ = sup S and k is an upper bound of S ⇒ k’ < k. ...(i)
Again k = sup S and k’ is an upper bound of S k ⇒ k' ...(ii)
From (i) and (ii), k = k’
Hence the set S has the unique supremum.
Example 9: Prove that the greatest member of a set, if it exists, is the supremum (l.u.b.) of the set.
An element G of a set S is called the greatest member of S if
(i) G ∈ S and
(ii) x < G ∀ x c S.Let G be the greatest member of S.
Then x < G ∀ x ∈ S and G is an upper bound of S.
Let G1 be any number < G, G ∈ S. Then G1 cannot be an upper bound of S.
(∵ G1 < G and G ∈ S). Hence G is the l.u.b. (supremum) of S.
Example 10: Show that the smallest member of a set, if it exists is the infimum (g.I.b) of the set.
An element g of a set S is called the smallest member of S if
(i) g ∈ S and
(ii) g < x ∀ x ∈ S.
Let g be the smallest member of a set S.Then g ∈ S and g < x ∀ x ∈ S ⇒ g is a lower bound of S.
Let g1 be any number > g.
Then g1 > g and g ∈ S ⇒ g1 cannot be a lower bound of S.
Hence g is the g.I.b. (infimum) of the set S.
Example 11: Define the notions supremum and infimum and distinguish them from the greatest and the least points. Give an example of a set of irrationals that has a rational supremum.
The infimum and supremum of a set may or may not belong to the set but the greatest and least points of a set must belong to the set. Indeed if the greatest and least points of a set S exist, then there are the supremum and infimum of S respectively.
The set
i.e.,
is a set of irrational members having 1 ∈ Q as the supremum.
Notice that
⇒
Completeness Of R
Properties of R as a Complete Ordered Field
The set R of real numbers satisfies the following properties :
A1 a ∈ R and b ∈ R ⇒ a + b ∈ R. (Closure law w.r.t. +)
A2 a + b = b + a ∀ a, b ∈ R. (Commutative law w.r.t. +)
A3 (a + b) + c = a + (b + c) ∀ a, b, c ∈ R. (Associative law w.r.t. +)
A4 a + 0 = a ∀ a ∈ R. (Existence of additive identity)
A5 To each a ∈ R, ∃ - a ∈ R such that a + (- a) = 0. (Existence of additive inverse)
M1 a ∈ R and b ∈ R ⇒ ab ∈ R (Closure law w.r.t. multiplication)
M2 ab = ba ∀ a, b ∈ R. (Commutative law w.r.t. multiplication)
M3 (ab) c = a (bc) ∀ a, b, c ∈ R. (Associative law w.r.t. multiplication)
M4 a . 1 = a ∀ a ∈ R. (Existence of multiplicative identity)
M5 For each 0 ≠ a ∈ R, ∃ a-1 ∈ R such that aa-1 = 1. (Existence of multiplicative inverse)
DL a (b + c) = ab + ac ∀ a, b, c ∈ R (Left Distributive law)
DR (b + c) a = ba + ca ∀ a, b, c ∈ R (Right Distributive law)
O1 For any a, b ∈ R, Exactly one of the following is true :
(i) a > b
(ii) a = b
(iii) b > a. (Trichotomy law)
O2 a > b and b > c ⇒ a > c ∀ a, b, c ∈ R. (Transitive law)
O3 a > b ⇒ a + c > b + c ∀ a, b, c ∈ R.
O4 a > b and c > 0 ac > bc.
The Order Completeness (O.C.) property of R :
Every non-empty set of real numbers which is bounded above, has the supremum in R.
The set R real numbers is a complete ordered field
The set of rational numbers is not order complete.
Example
Let S = {x : x ∈ Q. x > 0 and x2 < 2}.
S ≠ Φ (∵ 1 ∈ S) and 2 is an upper bound of S.
S is a non-empty bounded above subset of Q.
The Order Completeness Axioms [OC]
[OC1] The Lub Axiom : Every non-empty set S of ordered field F which is bounded above admits of (lub) supremum in F.
[OC2] The Gib Axiom : Every non-empty set S of ordered field F which is bounded below admits of (lub) supremum in F.
Thus, glb axioms ⇔ lub axioms
Complete Ordered Field
Definition : The ordered field F which when satisfies the above completeness axioms is called complete ordered field.
Explicit Statement of the properties of Real numbers which characterize the real number system as a complete ordered field :
1. The Field Axioms : A1 to A5 and M1 to M5 and DL, DR.
2. Order Axioms (>) : O1 to O4
3. Completeness Axioms : The lub axiom We shall call this complete ordered field as a field of real numbers and shall continue to denote by R.
Another Equivalent Completeness Axioms
Dedekind’s Completeness Axioms : If all the real numbers be divided into two subsets (classes) L and U of R then,
DC1 : Each subset has atleast one real number,
i.e., L ≠ Ф, U ≠ Ф
DC2 : Each real number either belongs to L or U.
i.e., L ∪ U = R
DC3 : Each member (real number) of class L is smaller than every member (real number) of class U,
i.e., if x ∈ L, y ∈ U ⇒ x < y.
then either the subset L has a greatest member or the subset U has a least member.
From the above axioms, complete ordered axioms can be deduced and conversely. These are equivalent.
Ordered complete axiom ⇔ Dedekind axiom
The Complete ordered field is also called Linear continuum and this is unique.
Let R1 and R2 be two complete ordered fields then we can always define one-one bijection between R1 and R2 such that ∀ x, y ∈ R.
f(x + y) = f(x) + f(y), f(x), f(y) e R2
and f(xy) = f(x) . f(y)
Clearly, f : R1 → R2
Here zero and identity elements of R1 are mapped on zero and identity elements of R2 respectively. This mapping is called Isomorphic mapping and R1 and R2 are called one-one isomorphic i.e., R1 ≅ R2 whose structure is also same. There may be difference of notation only.
Therefore if f(x) = x, then both the complete ordered field become same i.e., the complete ordered field is unique.
Theorem : The set Q of rational numbers is not a complete ordered field.
Theorem : A non-empty subset of real numbers which is bounded below has the greatest lower bound (infimum) in R.
Proof. Let S be any non-empty bounded below subset of R and k be its lower bound, then, k < x ∀ x ∈ S.
Let T = {-x : x ∈ S}. Then T ≠ Ф, as S ≠ Ф.
We shall prove that T is bounded above. We see that
k < x ⇒ -k > - x ∀ x ∈ S
⇒ (-x) < - k ∀ x ∈ S.
Thus T is bounded above with - k as its upper bound.
Since T is non-empty and bounded above, by order completeness property of R, T has supremum in R.
Let K = sup T.
⇒ (-x) < K ∀ x ∈ S ⇒ x > - K ∀ x ∈ S.
⇒ (-K) is a lower bound of S.
We shall now show that (-K) = inf S.
Let k’ be any lower bound of S. As shown above, -k’ is an upper bound of T. Since K = sup T ⇒ k < - k’ ⇒ - K > k’ ⇒ - K = inf S.
Hence S has the infimum in R.
Theorem : If S a non-empty set of real numbers which is bounded above, then a real numbers is the supremum of S if and only if the following two conditions holds
(i) x < s ∀ x ∈ S.
(ii) Given any ε > 0, ∃ some x ∈ S such that x > s - ε.
Proof. The condition is necessary.
Let s = sup S = l.u.b. S.
By definition, x < s, ∀ x ∈ S.
This proves condition (i).
Let ε > 0.
Then s - ε < s cannot be an upper bound of S.
So there exists some x ∈ S such that x > s - ε.
This proves condition (ii).
The condition is sufficient.
Let s be any real number satisfying conditions (i) and (ii).
We shall prove that s = sup S.
Now x < s ∀ x S ⇒ s is an upper bound of S.
Let, if possible s’ be any real number < s ⇒ s - s’ > 0.
Let ε = s - s’ > 0.
By condition (ii) ∃ some x ∈ S such that x > s - e = ε - (s - s’) = s’
⇒ x > s’ for some x ∈ S.
⇒ s’ is not an upper bound of S.
We see that no real number < s can be an upper bound of S.
Hence s = sup S.
Theorem : If S is a non-empty subset of R which is bounded below, then a real number t is the infimum of S iff the following two conditions hold :
(i) x > t ∀ x ∈ S.
(ii) Given any ε > 0, ∃ some x ∈ S such that x < t + ε.
Proof. The condition is necessary.
Let t = inf S = g.I.b. S.
⇒ x > t ∀ x ∈ S, which proves condition (i).
Let ε > 0 then, t + ε > t cannot be a lower bound of S.
So there exists some x ∈ S such that x < t + ε. This proves condition (ii).
The condition is sufficient.
Let t be any real number satisfying conditions (i) and (ii).
We shall prove that t = inf S.
Now x > t ∀ x ∈ S ⇒ t is a lower bound of S.
Let if possible t’ be any real number > t ⇒ t’ - t > 0.
Let ε = t’ - t > 0.
By condition (ii) ∃ some x ∈ S such that x < t + ε
⇒ x < t + (t’ - t) = t’ ⇒ x < t’ for some x ∈ S ⇒ t’ is not a lower bound of S.
We see that no real number > t can be a lower bound of S.
Hence t = inf S.
Example. Let S be a non-empty subset of R and s e R. Then s = sup S iff
(i) x < s ∀ x ∈ S
(ii) For each s’ e R such that s' < s, 3 some x ∈ S such that s’ < x.
Example. Let S be a non-empty subset of R and t e R. Then t = inf S iff
(i) x > t ∀ x ∈ S
(ii) For each t’ ∈ R such that t’ > t, 3 some x ∈ S such that t’ > x.
Representation of Real Numbers as Points on a Straight Line
The points on a straight line can be used to represent real numbers. Let X’ X be any straight line. Mark two points O and A on it such that A is to the right of O. The point O divides the straight line into two parts. We call the part that lies to the right of O as the positive part, and the part that lies to the left of O the negative part. Such a line for which positive and negative sides are fixed is called a directed line.
Suppose the points O and A represent the numbers 0 and 1, respectively. With OA as unity on a certain scale, we can locate all positive integers 1, 2, 3... on the right of O and all negative integers ..., -3, -2, -1 on the left of O. To represent any positive rational number m/n, we locate a point P on the right of O such that OP is m times the nth part of the unit length OA. Similarly, all negative rational numbers can be located on the left of O. The point on the straight line corresponding to rational numbers are called rational points. It might appear that rational points cover the entire straight line. But this is not true. There exist infinite number of points on the line which are not rational.
For Example, the point Q on the line such that OQ is equal to the diagonal of the square with side OA (OQ = √2 ) does not correspond to any rational number. Such points on the line which are not rational indeed fill up the gaps between the rational points are called irrational points and these correspond to irrational numbers. In this way every real number can be represented as a point on the straight line. On account of this representation, we refer to a real number as a point of R and the straight line is referred to as real line.
Dedekind-Cantor Axiom
To every real number corresponds a unique point on a directed line and to every point on a directed line corresponds a unique real number.
Absolute Value of Modulus of a Real Number
Definition. Let a be any real number. The absolute value or modulus of a, denoted by I a I, is defined as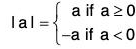
Remarks
1. | a | > 0 a ∈ S.
2. | a | = | - a |.
Theorem : If a is any real number, then I a I = max {a, -a}.
Proof. We have
|a| = a, if a > 0, ...(1)
and |a| = -a > a, if a < 0. ...(2)
From (1) and (2), we get |a| > a.
Again lal = a > - a, if a > 0, ...(3)
and lal = -a, if a < 0. ...(4)
From (3) and (4), we get lal > - a.
Hence lal is the maximum of the two real numbers a and -a i.e.,
lal = max {a, - a.}
Theorem. If x, y ∈ R ; then
(i) Ixl2 = x2 = I—x|2.
(ii) Ixyl = Ixl . lyl.
(iii) 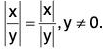
(iv) lx + yl2 + lx - y|2 = 2 (Ixl2 + lyl2).
Proof. (i) if x > 0 then Ixl = x ⇒ Ixl2 = x2,
and if x < 0, then Ixl =-x ⇒ Ixl2 = (-x)2 = x2.
Thus Ixl2 = x2.
Similarly, we can prove that I -x|2 = x2.
(ii) Using (i), Ixyl2 = (xy)2 = x2y2 = lxl2.lyl2 = (Ixl.lyl)2
Ixyl = ± (|x|.|y|).
Since Ixl is non-negative ∀ x ∈ R, therefore
Ixyl = Ixl.lyl.
(iii) Using (i) 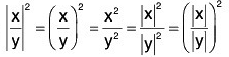
∴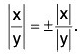
Since Ixl is non-negative ∀ x ∈ R, therefore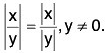
(iv) lx + yl2 + lx - y|2 = (x + y)2 + (x - y)2, by part (i)
= 2 (x2 + y2)
= 2 (Ixl2 + lyl2), by part (i)
Theorem . If x, y are any two real numbers, then
(i) lx + yl < Ixl + lyl (Triangle Inequality)
(ii) lx -y| >llxl -|y||.
(iii) lx - y| < Ixl + lyl.
Proof. (i) To show lx + yl < Ixl + lyl.
Case I. Let x + y > 0 ⇒ lx + yl = x + y, by definition
< Ixl + lyl (∵ x < Ixl ∀ x ∈ R)
lx + yl < Ixl + lyl.
Case II. Let x + y < 0 ⇒ lx + yl = - (x + y) = (-x) + (-y).
Since -x < Ixl ∀ x ∈ R, lx + yl < Ixl + lyl.
Hence lx + yl < Ixl + lyl.
Aliter. We know
lx + yl2 = (x + y)2 = x2 + y2 + 2xy = Ixl2 + yl2 + 2xy
or lx + yl2 < Ixl2 + yl2 + 2 Ixl lyl (v xy < Ixyl = Ixl lyl)
lx + yl2 < (Ixl + lyl)2.
Hence lx + yl < Ixl + lyl, since modulus is non-negative.
(ii) To show lx - y| > llxl - |y||.
We have Ixl = lx - y + y < lx - y| + |y|
⇒ Ixl - |y| < lx - y|. ...(1)
Again lyl = ly - x + x| < ly - x| + |x|
⇒ lyl - |x| < I -(x - y) |
⇒ (|x| - |y|) < lx - y|. ...(2)
From (1) and (2), lx - y| > Ixl - |y|,
and lx - y| > - (|x| - |y|).
∴ lx - y| > max {(Ixl - |y|), - (|x| - |y|)}.
Hence lx - y| > llxl - |y||.
(∵ max {a, -a} = |a| ∀ x ∈ R)
(iii) x - y| = |x + (-y)| < Ixl + I—y| = |x| + |y|.
Hence lx - y| < Ixl + lyl.
Example 12: If x and y are real numbers and ε > 0,
(i) Show that lx - y| < ε if and only if y - ε < x < y + ε.
(ii) Show that Ixl < a ⇔ - a < x < a.
(i) We know lal = max {a, -a} ∀ x ∈ R.
∴ lx - y| = max {(x - y), -(x - y)} = max {x - y, y - x}.
It follows that lx - y| < ε
⇔ max {x - y, y - x} < ε
⇔ x - y < ε and y - x < ε⇔ x < y + ε and y - ε < x
⇔ y - ε < x < y + ε.
(ii) Ixl = max {x, -x} < a
⇔ x < a and -x < a
⇔ x < a and x > - a⇔ - a < x and x < a
⇔ -a < x < a.
Example 13: Show that for all real numbers x and y,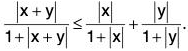
We know lx + yl < Ixl + lyl
⇒ 1 + lx + yl < 1 + Ixl + lyl
⇒
⇒
(∵ 1 + Ixl + lyl > 1 + Ixl and 1 + Ixl + lyl > 1 + lyl)
Example 14: If x1, x2, xn are real numbers, then show that
(i) lx1x2... xnl = lx1l lx2l ... Ixnl.
(ii) lx1 + x2 + ... + xnl < Ix1l + lx2l + ... + lxnl.
(i) lx1x2 ...xnl = Ix1l lx2x3 ... xn) (∵ Ixyl = Ixl lyl)
= Ix1I lx2l IX3 ... xnl, and so on
Thus lx,x0 ...x I = IxJ IxJ ... lx I.(ii) x1 + x2 + ... + xnl = lx1 + (x2 x3 + ... + xn)l
< Ix1l + lx2 + x3 + ... + xnl
(∵ lx + yl < Ixl + lyl)
< Ix1l + lx2l + x3 + ... + xnl, and so on
Thus lx1 + x2 + ... + xnI < lx1l + Ix2I + ... + lxnI.
Example 15: Show that
(i) lx + yl > 1 ⇒ Ixl >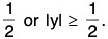
(ii) lx1 + x2 + ... + xnl > 1 ⇒ IxiI > 1/n for some i with 1 < i < n.
(i) Suppose the conclusion is false. Then
Now lx + yl < Ixl + lyl <
⇒ lx + yl < 1, a contradiction.
Hence
(ii) Suppose the conclusion is false. Then
for each i with 1 < i < n.
Now lx1 + x2 + ... + xnl < Ix1I + Ix2I + ... + IxnI
∴ lx1 + x2 + ... + xnI < 1, a contradiction.
Hence
for some i with 1 < i < n.
|
98 videos|34 docs|32 tests
|
FAQs on Point Set Topology - I - Mathematics for Competitive Exams
| 1. What is point set topology and how is it related to IIT JAM? |  |
| 2. What are some basic concepts in point set topology that are important for IIT JAM preparation? |  |
| 3. How can point set topology be applied to real-world problems? |  |
| 4. What are some recommended study resources for point set topology for IIT JAM preparation? |  |
| 5. How can I effectively prepare for point set topology in the IIT JAM exam? |  |