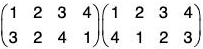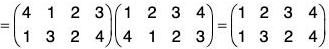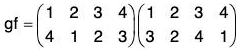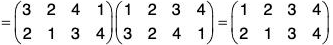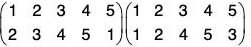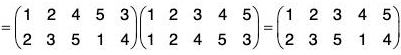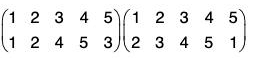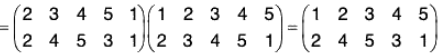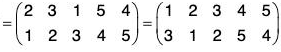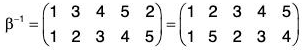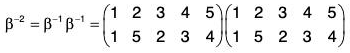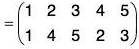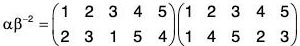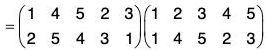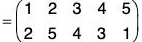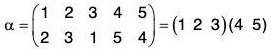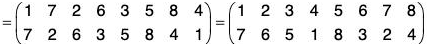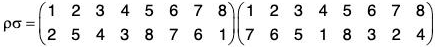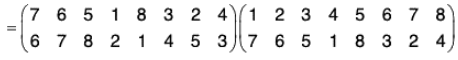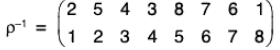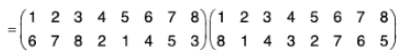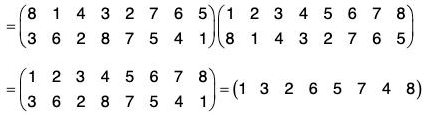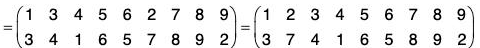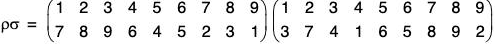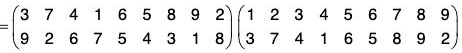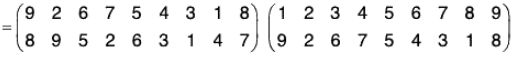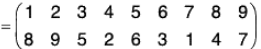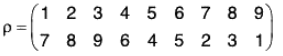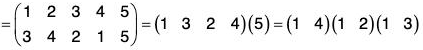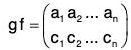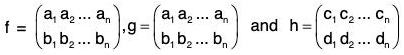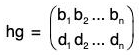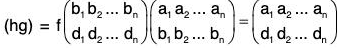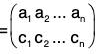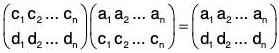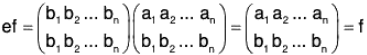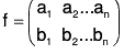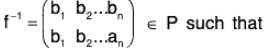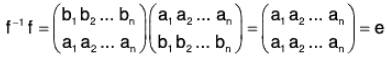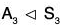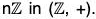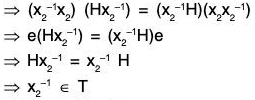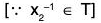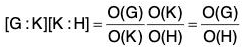Group Theory- III | Mathematics for Competitive Exams PDF Download
| Table of contents |

|
| Permutation |

|
| Dihedral Group |

|
| Cosets |

|
| Lagrange's Theorem And Consequences |

|
Permutation
Transformation
A transformation of a set A is a bijection from A to A i.e. itself.
Thus a function f defined on A is a transformation of A if,
(i) f : A → A. i.e., range of f is obtained in A
(ii) f is an injection i.e. a one-one map
and (iii) f is a surjection i.e. an onto map.
Permutation : Definition
A transformation of a finite set S is called a permutation on S i.e. a permutation is a bijection on a finite set S.
Notations: Two row notation
Let A = {a1, a2, ..., an} be a finite set of n distinct elements. Then it is denoted by two row notation as follows :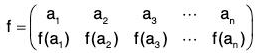
In this notation, the f-image of each element of the upper row written just below it in the lower row, because f is bijective on A.
Therefore all the n elements of A are obtained in some other or in the lower row.
For example, a function f is defined on the set {1, 2, 3, 4} as follows :
f(1) = 2, f(2) = 3, f(3) = 4, f(4) = 1,
then 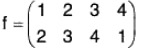
Equality of two permutations :
The permutation which maps every element of a set to itself, is called identity permutation. Symbolically, it is denoted by 1.
If set A = {a1, a2, a3......an),
then 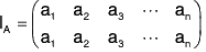
Examples of Permutation :
Example : If A = {a, b}, then all the functions that can be defined from A into A are :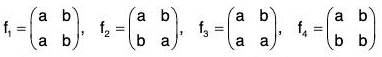
Evidently f1 and f2 are permutations of A but f3 and f4 are not (being many one).
Example : Let f = 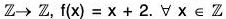 We notice that for any two elements a and b of
We notice that for any two elements a and b of 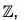
a ≠ b ⇒ a + 2 ≠ b + 2 ⇒ f(a) ≠ f(b)
Therefore f is one one.
Again the pre-image of every element x of the codomain 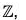 is (x - 2) which exists in the domain
is (x - 2) which exists in the domain 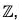 . Therefore f is onto.
. Therefore f is onto.
Therefore f is a bijection on 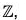
Consequently, f is a permutation on 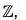
Example : Let A = {1, -1, i, -i} and f be defined as f(x) = i x for every x ∈ A.
Then f is a permutation.
Since A is a finite set, if we write f in the standard notation as given above, then 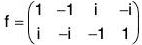
As all the elements of lower row are the same as those of the upper row and no element is repeated, f is a permutation of given set A.
Example : Let A = {0, 1, 2, 3} and
f : A → A,
f(x) = x +4 2
then 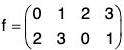 Clearly f is a permutation on A.
Clearly f is a permutation on A.
Example : Let G be a finite group and corresponding to any a of G, a function fa is defined in G as
fa(x) = ax ∀ x ∈ G
∵ a ∈ G, x ∈ G ⇒ ax ∈ G
∴ fa : G → G
We see that fa(x) = fa(y) ⇒ ax = ay
⇒ x = y [by left cancellation law]
∴ fa is a one one map.
Again, for every element x of G, an element a-1x exist in G such that fa(a-1x) = a(a-1x)
= (aa-1)x = ex = x
∴ fa is an onto map.
Since fa is bijection on G, therefore this is a permutation on G.
Important Remark : If any finite set A contains n elements, then every permutation of A is of degree n and number of permutations of A is n!.
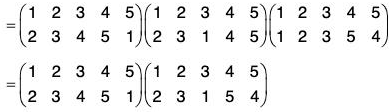
Product or Composite of permutations
If f and g be the two permutations of any set A, then by the product of two permutations f g we mean to find their composite function f o g. Therefore for any x ∈ A
fog(x) = (fog)(x) = f[g(x)]
For example, if 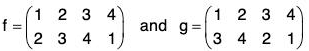 be two permutations of the set {1, 2, 3, 4}, then
be two permutations of the set {1, 2, 3, 4}, then
fg(1) = fog(1) = f[g(1)] = f(3) = 4
fg(2) = fog(2) = f[g(2)] = f(4) = 1
fg(3) = fog(3) = f[g(3)] = f(2) = 3
fg(4) = fog(4) = f[g(4)] = f(1) = 2
Therefore f g = fog = 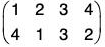
If the order of the upper row in f is made same as the order of the lower row in g, then the lower row of fog is the lower row of f and upper row in fog is the lower row of f and upper row in fog is the upper row of g. Thus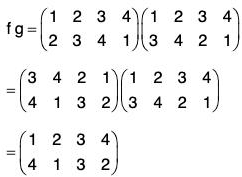
Similarly gf = 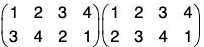
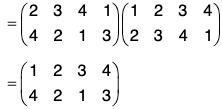
By the calculations of f g and g f, we observe that
f g ≠ g f
i.e. the product of the permutations is not commutative.
Associativity : The associative law is true for the product of the permutations i.e. f, g and h are permutations, then (f g) h = f(g h)
Inverse Permutation :
If the product of the two permutations is an identity permutation, then they are called inverse permutation of each other.
For example : The permutations 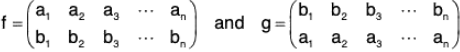 are mutually inverse as fg = gf = 1
are mutually inverse as fg = gf = 1
Remark. The inverse permutation can be obtained by interchanging the rows of the given permutation.
Group of Permutations
The set of all the permutations of a given non empty set A is denoted by SA. Therefore if A = {a, b}, then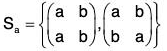
If A = {a, b, c}, then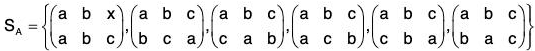
It can be easily seen that
O(A) = n ⇒ O(SA) = n!
In the following theorem we prove that SA is a group for the product of permutations.
Theorem : The set SA of all permutations of a non void set A is a group for the product of permutations.
Proof. Since the composition of two bijections is also a bijection, so the product of any two permutations of a set will always be a permutation of that set.
∴ f ∈ SA, g ∈ SA fg ∈ SA
i.e., SA is closed for the product of permutations.
Verification of Group axioms in SA :
- [G1] Since the composite of function is associative, therefore for any
f, g, h ∈ SA
(fg)h = (fog)oh
= fo(goh) = f(gh)
Therefore the product of permutations is associative. - The identity permutation lA ∈ SA is the identity for the composition because for every
f ∈ SA
(lA f)(x) = lA[f (X)] = f(x)
and (f lA)(x) = f[lA(x)] = f(x) - Let f ∈ SA, then
f ∈ SA ⇒ f : A → A is bijection
⇒ f-1 : A → A is also bijection
⇒ f-1 ∈ SA
which is the inverse of f because f f-1 = lA = f-1 f
Therefore the inverse of every permutation exist in SA.
From the above discussion, it is proved the SA is a group for the product of permutations.
Permutation Group Definition
The set of all permutations SA of a non void set A is a group for the product of permutations which is called the permutation group of A.
Remark : If A is a finite set of cardinal n i.e. consisting of n distinct elements, then SA is a group of order n! and in that case it is generally denoted by PA.
Note. SA is a non commutative group because the composition of functions is not commutative.
Symmetric Group
The group of permutation of set {1, 2, ..., n} is called the symmetric group of degree n. It is denoted by Sn.,
An important Symmetric group (S3) :
Since all the groups of order less than or equal to 5 are abelian, S3 is the first non-abelian group. If A = {1, 2, 3}, then there will be following 6 permutations of A :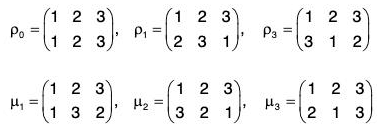
Therefore S3 = {ρ0, ρ1, ρ2, μ1, μ2, μ3}
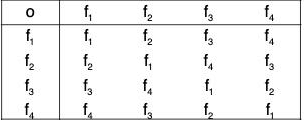
Composition Table for S3 :
Calculating all the possible product of permutations of S3, we obtain the following composition table :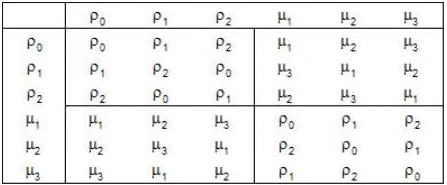
From the above table we observe that
(i) All the elements are the members of S3. Therefore S3 is closed for the product of permutations.
(ii) ρ0 is the identity permutation in S3.
(iii) ρ0, ρ1, ρ2, μ1, μ2, μ3 are inverse of ρ0, ρ1, ρ2, μ1, μ2, μ3 respectively.
(iv) The table is not symmetrical wrt the principal diagonal.
Again the product of permutations is associative.
Therefore S3 is a finite non abelian group of order 6.
Remark. It can also be easily observed from the above composition table of S3 that the set {ρ0, ρ1, ρ2} of S3 also satisfies all the axioms of a group.
Therefore this is also a group which is called the subgroup of S3.
Cyclic Permutations or Cycles
A permutation a of a set A is a cyclic if there exists a finite subset {a1, a2, .... ar} of A such that:
σ(a1) = a2, σ(a2) = a3, .... σ(ar) = a1
Therefore σ(x) = x, if x ∈ A. But x ∉ {a1, a2, .... ar}
If σ is such a permutation, then we denote it by σ = (a1 a2 a3 ... ar) in which σ-image of every element is its next element and the o-image of the last element is the first element.
Again the number of elements in this row notation is called the length of the cycle σ.
For example, σ = (2 4 5 6) ∈ S6 is a cycle of length 4 where σ(2) = 4, σ(4) = 5, σ(5) = 6, σ(6) = 2 and σ(1) = 1, σ(3) = 3.
Thus, clearly 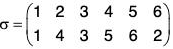
Remarks :
- The length of the identity permutation is 1 which can be represented by an element of the set.
Example : The identity permutation of S3 may also be represented by (2) or (3) - The product of two cycles may be obtained by writing the corresponding permutations and then multiplying by the product method.
- A cycle may be written in many ways by maintaining the cyclic order e.g. (1 2 3) = (2 3 1) = (3 1 2)
Order of a Cycle
For the above cycle σ(2456) ∈ S6, we notice that
σ(2) = 4, σ2(2) = 5, σ3(2) = 6, σ4(2) = 2.
Similarly,
σ4(4) = 4, σ4(5) = 5, σ4(6) = 6, σ4(1) = 1, σ4(3) = 3.
Clearly σ4 is the identity permutation which is the identity element of S6.
∴ From the group S6, O(σ) = 4.
Therefore it can be proved that the order of any cycle is equal to its length i.e., the order of a cycle of length r is r.
Inverse of a Cycle
The permutation obtained by writing the elements of any permutation σ in the reverse order is called its inverse permutation. It is represented by σ-1.
For example, If s = (2 4 3 5), then σ-1 = (5 3 4 2)
Disjoint Cycles
Two cycles are said to be disjoint if the set of numbers that represent the cycles have no common element.
From the definition, it is clear that those element permuted by one is not permuted by the other.
For example. The permutations ρ = (2 3 4) and σ = (15) are disjoint in S5 whereas φ = (3 5 2) and ψ = (1 2 4) are not disjoint cycles because 2 is in both the notations φ and ψ.
Product of Disjoint Cycles
From the above definition of disjoint cycles, we have seen that if ρ and σ are disjoint cycles of same degree, then the elements that are permuted by ρ are not permuted by a and vice versa. Therefore for any x,
ρ(x) ≠ x ⇒ σ(x) = x ⇒ ρσ(x) = ρ(x)
and σ(x) = x ⇒ ρ(x) ≠ x ⇒ σφ(x) = ρ(x)
∴ ρσ(x) = σρ(x)
Similarly, it can be seen that when σ(x) ≠ x, then
ρσ(x) = σρ(x)
which conclude that ρσ = σρ,
i.e. The product of any two disjoint cycles is commutative.
For example, If ρ = (125) = σ = (345) are two disjoint cycles in S6, then
ρσ = (1 2 5)(3 4 6)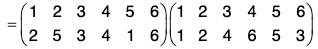
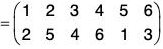 ...(a)
...(a)
and ρσ = (3 4 6)(1 2 5)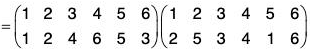
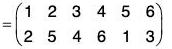 ...(b)
...(b)
From (a) and (b), it is clear that, ρσ = σρ
Theorem : Every permutation can be expressed as the product of disjoint cycles.
Proof. Let σ be a permutation of a finite set A. Taking any invariant element a of A, obtain a row where first element is a, next element is σ(a), further next element is σ(σ(a))....Since the number of elements in A are finite, therefore after some steps, we obtain an element whose σ-image is a. Thus this row will represent a cycle. If all the elements of A are not included in this cycle, then taking any element b from the remaining elements, obtain another cycle as above.
Continue this process till all the elements of A are included in any of these cycles. Since A is finite, therefore the number of these cycles of σ will also be finite. Again no element is common in any two cycles, therefore the permutation σ is expressible as the product of some finite disjoint cycles.
Remark. In the above product of disjoint cycles, if a cycle of length 1 is obtained, then it is not written.
For example, if 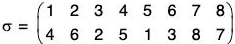 then
then
σ = (1 4 5)(2 6 3)(7 8)
Order of a permutation
The order of a permutation of a finite set is the L.C.M. of the order of its disjoint cycles.
We have seen that the degree of any cycle is equal to its length.
Also since every permutation can be expressed as the product of disjoint cycles, therefore it can be easily seen that
O(f) = L.C.M. of lengths of disjoint cycles of f.
For the above permutation σ
O(σ) = L.C.M. of {O(1 4 5), O(2 6 3), O(7 8)}
= L.C.M. of {3, 3, 2} = 6.
Transposition
A cyclic permutation of length two (2) is called a transposition.
For example, the cycles (a, b), (1, 2), (2, 3) etc are transposition.
It can be easily seen that every transposition is its own inverse
Every permutation is a product of transpositions :
With the help of product of permutations, it can be easily seen that for any cycle.
(a1 a2 a3 ... an-1 an)
(a1 a2 a3 ... an-1 an) = (a1 an)(a1 an-1) ... (a1 a3)(a1 a2)
Therefore every cycle can be expressed as the product of transpositions, but we have seen that every permutation can be written as the product of disjoint cycles.
Hence every permutation can be expressed as the product of transpositions.
Example : If 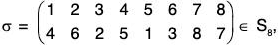 then
then
σ = (1 4 5)(2 6 3)(7 8)
= (1 5)(1 4)(2 3)(2 6)(7 8)
Finally it should be noted that this representation as a product of transpositions is not unique.
But it can be proved that the number transpositions in the product will always be even or odd i.e. the number of transpositions in this type of factorisation of any permutation σ is even (odd), then the number of transpositions of every factorisation of the permutation σ will also have the same even (odd).
On the basis of this nature of number of transpositions even (odd), the even and odd permutation will be defined.
Inversion : If σ ∈ Sn, then the pair (i, j), 0 < i < j ≤ n, is an inversion for σ if σ(i) > σ(j)
Signature : The total number of such inversions for the permutation o is called its signature and we write it as sig σ.
Example : If a = 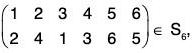 then 2 >1 ,4 > 1,4 >3, 6 > 5. Therefore (13), (23), (24, (56) are the inverses of σ. Hence sig σ = 4.
then 2 >1 ,4 > 1,4 >3, 6 > 5. Therefore (13), (23), (24, (56) are the inverses of σ. Hence sig σ = 4.
Even and odd permutations
A permutation is said to be an even permutation if it can be expressed as a product of an even number of transpositions; otherwise it is said to be an odd permutation, i.e. it has an odd number of transpositions.
Example : The permutation 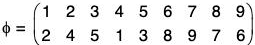 is an even permutation because
is an even permutation because
φ = (1 2 4)(3 5)(6 8 7 9)
= (1 4)(1 2)(3 5)(6 9)(6 7)(6 8)
= product of 6 (even) transpositions.
Example : The permutation ψ = 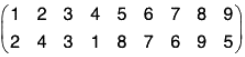 is an odd even permutation because
is an odd even permutation because
ψ = (1 2 4)(3)(5 8 9)(6 7)
= (1 4)(1 2)(5 9)(5 8)(6 7)
= product of 5 (odd) transpositions.
Remarks :
- A cycle of length n will be even (odd) if n is odd (even).
- Identity permutation is an even permutation because this can be written as the product of two transpositions (sig lA = o)
- Every transposition is an odd permutation
Product and Inverse of Even or Odd permutations
For any two permutations α, β of any set, if α is a product of p transpositions and β is a product of q transpositions, then clearly,
α, β will be the product of (p + q) transpositions and α-1 will be the product of p transpositions.
Therefore if p and q both are even or both are odd, then (p + q) will be even.
Consequently, α, β will also be an even permutation.
Similarly if p is odd (even), then (p + q) will be odd.
Consequently, α, β will be an odd permutation.
From the above discussion, we arrive at the following conclusions :
(i) The product of two even (odd) permutations is an even permutation.
(ii) The product of one even (odd) and one odd (even) permutation is an odd permutation.
(iii) The inverse of an even (odd) permutation is even (odd) permutation.
Alternating group (Group of even permutation)
On the basis of the above conclusions of the product of even and odd permutations of any set, we will show that the set of permutations is also a group.
Theorem : The set A n of all even permutations of degree n is a group of order (1/2)n!
for the product of permutations.
Proof. Since the product of two even permutations is even, An is closed for the multiplication composition of permutations.
Verification of group axioms in An :
- [G1] : ∴ Multiplication of permutations is associative, so also for An.
- [G2] : ∵ The Identity permutation I is an even permutation, therefore the identity permutation e of order n is the identity element in An.
- [G3] = ∵ The inverse of every even permutation is also even,
∴ α ∈ An ⇒ α-1 ∈ An which is the inverse of α.
Therefore inverse of every element exist in An.
∴ An is a group for the product of permutations.
Order An :
Let An = {α1, α2...... αm} and Bn = {β1, β2, .... βr}
where Bn is a set of odd permutations of order n.
∴ O(An) = m and O(Bn) = r
But O(An) + O(Bn) = O(Sn)
∴ m + r = n! ...(1)
If β ∈ Bn then in the product
βα1, βα2, ... βαm
each permutation will be odd and no two product will be same, because
βαi, = βαj, ⇒ αi = αj
∴ {βα1, βα2,... βαm} ⊂ Bn
⇒ O{βα1, βα2,... βαm} ≤ O(Bn)
⇒ m ≤ r ...(2)
Similarly it can be seen that
{ββ1, ββ2, ... ββr} ⊂ An
⇒ {ββ1, ββ2, ... ββm} ≤ O(An)
⇒ r ≤ m ...(3)
∴ (2) and (3) ⇒ r = m ...(4)
Now (1) and (4) ⇒ r = m = (1/2)n!
O(An) = (1/2)n!
Note : An is called the alternating group of degree n.
Important Results :
- When n = 3, then A3 = {(1),(1 2 3),(1 3 2)}
- An is a simply group for n ≥ 5
Every group of prime order is a simple group because such group has no proper subgroup. - The set of odd permutations of degree n is not a group because it is not closed for multiplication.
- If H is a sub group of G and
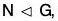 , then H ∩ N need not be normal in G.
, then H ∩ N need not be normal in G.For example, let
N = A4 = {(1), (123), (124), (132), (134), (142), (143), (234), (243), (12), (34), (13), (24), (14) (23)}
H ={(1), (1234), (13)(24), (1432), (12)(34), (14)(23), (13)(24)}
This can be easily verified that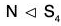 and H is a subgroup of S4.
and H is a subgroup of S4.
But H ∩ N is not a normal subgroup of S4. - S3/A3 is a commutative and cyclic group, being group of order 2 but S3 is non abelian and not a cyclic group.
Since A3 is normal subgroup of S3 therefore quotient group exist
Now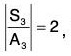 which is prime number.
which is prime number.
⇒ Quotient group S3/A3 is cyclic
⇒ Quotient group S3/A3 is Abelian (Every cyclic group is abelian)
Theorem : The alternating group An of all even permutations of degree n is a normal subgroup of the symmetric group Sn.
i.e. 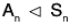
Proof. We know that An is a subgroup of Sn
Let α ∈ Sn and β ∈ An. If α is an even permutation, then α-1 will also be even permutation.
Hence αβα-1 will also be an even permutation.
If α is an odd permutation, then α-1 will also be odd.
∴ αβα-1 ∈ An.
If α is odd permutation, then α-1 will also be odd.
Hence αβα-1 will be an even permutation.
Thus under all the circumstances, we see that α ∈ Sn, β ∈ An ⇒ αβα-1 ∈ An.
∴ An is a normal subgroup of Sn i.e,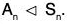
Example : Find fg and gf when :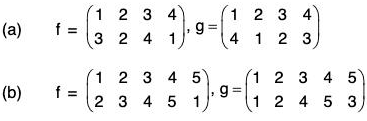
(a) fg =
= (2 3)
and
= (1 2)
(b) fg =
= (1 2 3 5 4)
and gf =
= (1 2 4 3 5)
Example : If α = 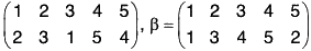
Compute the following: (a) α-1 (b) αβ-2 (c) O(α)
(a) α-1
(b)
∴
Therefore
(c) ∵
∴ O(a) = L.C.M. of {O(1 2 3), O(4 5)}
= L.C.M. of {3, 2}
Example : If σ = (1 7 2 6 3 5 8 4) and ρ = 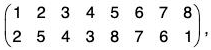 then prove that :
then prove that :
ρσρ-1 = (ρ(1) ρ(7) ρ(2) ρ(2) ρ(6) ρ(3) ρ(5) ρ(8) ρ(4))
∵ σ = (1 7 2 6 3 5 8 4)
∴...(1)
Again
∴ ρσρ-1 = (ρσ)ρ-1
= (2 6 5 7 4 8 1 3)
= (ρ(1) ρ(7) ρ(2) ρ(6) ρ(3) ρ(5) ρ(8)ρ(4))
Example : If ρ = 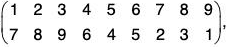 σ = (1 3 4)(5 6)(2 7 8 9) then find σ-1 ρσ and by expressing the permutation ρ as the product of disjoint cycles, find whether ρ is an even permutation or odd permutation. Also find its order.
σ = (1 3 4)(5 6)(2 7 8 9) then find σ-1 ρσ and by expressing the permutation ρ as the product of disjoint cycles, find whether ρ is an even permutation or odd permutation. Also find its order.
σ = (1 3 4)(5 6)(2 7 8 9)
∴...(1)
Again...(2)
σ-1ρσ = σ-1(ρσ)
= (1 8 4 2 9 7) (3 5 6)
Again
= (1 7 2 8 3 9)(4 6 5)
= (1 9)(1 3)(1 8)(1 2)(1 7)(4 5)(4 5)
= product of 7 (odd) transpositions.
Since ρ is equal to the product of odd transpositions, therefore this is a odd permutation.
Finally, O(p) = L.C.M. of {O(1 7 2 8 3 9), 0(4 6 5)}
= L.C.M. of {6, 3}
= 6
Example : Express the following permutations as the product of disjoint cycles. Also find whether these permutations are even or odd.
(a) 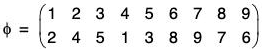
(b) ψ = (1 2 3 4 5)(1 2 3)(4 5) ∈ S5
(a) We see that
φ = (1 2 4)(3 5)(6 8 7 9)
Again ( 1 2 4) = (1 4)(1 2)
and (6 8 7 9) = (6 9)(6 7)(6 8)
∴ φ = (1 4)(1 2)(3 5)(6 9)(6 7)(6 8)
= product of 6 (even) transpositions.
Therefore φ is an even permutation.
(b) We see that
ψ = (1 2 3 4 5)(1 2 3)(4 5)
= product of 3 (odd) transpositions.
Therefore ψ is an odd permutation.
Example : Show that the set of the permutations (a), (ab), (cd), (ab) (cd) of the set {a, b, c, d} forms a group for the product of permutations.
Let (a) = f1, (ab) = f2, (cd) = f3, (ab)(cd) = f4 and G = {f1, f2, f3, f4}
Calculating the products of permutations of G,
f1 f2 = f2, f1 f3 = f3, f1, f4 = f4, f2 f1 = f2, f3 f1 = f3, f4 f1 = f4
f2 f2 = (ab)(ab) = f1
f2 f3 = (ab)(cd) = f4
f2 f4 = (ab)(ab)(cb) = (cd) = f3
f3 f2 = (ad)(ab) = (ab)(cd) = f4
f3 f3 = (cb)(cd) = f1
f3 f4 = (cd)(ab)(cd) = (ab) f2
f4 f2 = (ab)(cd)(ab) = (cd) f3
f4 f4 = (ab)(cb)(ab)(cd) = f1
From the above products, the composition table of G is :
Observing the table, it is clear that :
(i) All its elements are in G, therefore G is closed for the multiplication of permutations.
(ii) f1 is the identity element.
(iii) Every element is inverse of itself.
Again the multiplication of permutation is associative, therefore this is associative in G also.
Hence G is a group for the multiplication of permutation s.
Example : Show that the set A3 = {(a), (a b c), (a c b )} of even permutations of the set {a, b, c} is a group for the product of permutations.
Calculating the possible product in A3
(a)(a) = (a), (a)(a b c) = (a b c), (a)(a c b) = (a c b) (a b c)(a) = (a b c)(a b c); (a b c) = (a c b), (a b c)(a c b) = (a) (a c b)(a) = (a c b)(a c b); (a b c) = (a), (a c b)(a c b) = (a b c) Therefore, the composition table of A3 is as follows:
Observing the table,
- All its elements are in A3,
Therefore A3 is closed for the multiplication of permutations- The identity element (a) exists.
- The inverses of (a), (abc), (acb) are respectively (a), (acb), (abc).
Again multiplication of permutations is associative, there fore it is in A3 also. Hence A3 is a group for the multiplication of permutation.
Example : Prove that the set Pn of all permutations of degree n is a group of order n! for the product of permutations.
Let S = {a1, a2, ..., an} be a finite set of n elements. There fore every permutation of S is of n degree. Since n elements of S can be arranged in n! ways, there fore the total number of permutations is equal to the number of permutations n! of degree n. Let Pn be the set of all the permutations of degree n.
Letbe any two permutations of degree n. Since b1, b2, .... bn and c1, c2, .... cn, are only different arrangements of n elements of S, there fore elements of first row (keeping the column sun altered) in g are arranged in the same order in which the elements appear in the second row of f. Now by multiplication of permutations,
which is a permutation of degree n.
Therefore g ∈ Pn, f ∈ Pn ⇒ g f ∈ Pn
∴ Pn is closed for the multiplication of permutation.Verification of group axioms in Pn :
[G1] Let
be any three permutations of degree n where
b1, b2, ..., bn; c1, c2 ... cn; d1, d2, ... dn
are different arrangements of elements of S
Then
∴
and g f
∴ h(g f) =
Thus (hg)f = h(gf)
which shows that the multiplication of permutations is associative.
[G2] Let e =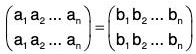
be the identity permutation of degree n, therefore e ∈ Pn such that
and
Therefore the identity permutation of degree n exist in Pn.
[G3] Let
Then
and
Therefore f-1 is the inverse of f wrt multiplication of permutations.
Therefore inverse of every element exist in Pn.
From the above discussion, Pn is a group for the multiplication of permutations. Again since the total number of permutations in Pn is n!. Therefore this is a group of order n!.
Example : If A = {a, b, c, d} and SA is the permutation group of A, then prove that Ta = {ρ ∈ SA; ρ(a) = a} is a sub group of SA.
By definition, Ta contains those permutations of SA where the image of a is a. Therefore Ta will contain the following permutations :
ρ1 = (a). ρ2 = (bed), ρ3 = (bde)
ρ4 = (be), ρ5 = (cd), ρ6 = (bd)
∴ TA = {ρ1, ρ2, ρ3, ρ4, ρ5, ρ6}
Multiplying the permutations, the composition table of Ta is as follows :
Observing the table, it is clear that all its elements are in Ta.
Therefore Ta is closed for the multiplication of permutations
i.e., x ∈ Ta, y ∈ Ta ⇒ xy ∈ Ta
Therefore by theorem Ta is a subgroup of SA.
Example : Find the quotient group G/H and also prepare its operation table when G = S3 and H = A3.
We know that
S3 = {(1), (123), (132),(12), (23), (32)}
and A3 = {(1), (123), (132)}
We have earlier proved that
Therefore S3/A3 exist.
The following cosets of A3 are obtained in S3 :
(1) A3 = A3(1) ={(1)(1), (123)(1), (132)(1)}
= {(1), (123), (132)} = A3.
(123)A3 = A3(123) = {(1), (123), (123)(123), (132)(123)}
= {(123), (132), (1)} = A3.
(132)A3 = A3(132) = {(1)(132), (123)(132), (132)(132)}
= {(132), (1), (123)} = A3.
(12)A3 = A3(12) = {(1),(12), (123)(12), (132)(12)}
= {(12), (13), (23)}
(23)A3 = A3(23) = {(1) (23), (123) (23), (132) (23)}
= {(23), (12),(31)}, = A3(12).
(31)A3 = A3(31) = {(1)(31), (123)(31), (132)(31)}
= {(31 ),(23),(12)} = A3(12).
Thus we see that
G/H = S3/A3 = {A3, A3}(12)}
Its composition table is as under :
Dihedral Group
Another special type of permutation group is the dihedral group. Such group consist of the rigid motions of a regular n-sided polygon or n-gon. For n = 3, 4, ..., we define the nth dihedral group to be the group of rigid motions of a regular n-gon. We will denote this group by Dn. We can number the vertices of a regular n-gon by 1, 2, ..., n (Figure). Notice that there are exactly n choice to replace the first vertex. If we replace the first vertex by k, then the second vertex must be replaced either by vertex k + 1 or by vertex k - 1; hence, there are 2n possible rigid motions of the n-gon. We summarize these results in the following theorem.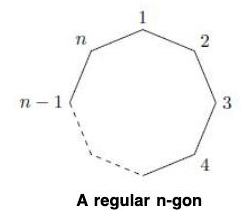
Theorem : The dihedral group, Dn, is a subgroup of Sn of order 2n.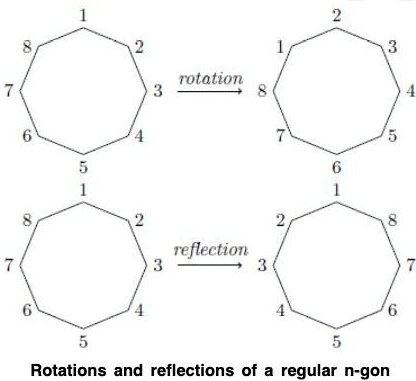
Theorem : The group Dn, n > 3, consists of all products of the two elements r and s, satisfying the relations
rn = e
s2 = e
srs = r-1.
Proof : The possible motions of a regular n-gon are either reflections or rotations (Figure). Therefore are exactly n possible rotations: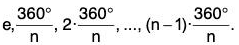
We will denote the rotation 360°/n by r. The rotation r generates all of the other rotations. That is,
rk = k.(360°/n)
Label the n reflections s1, s2, .... sn, where sk is the reflection that leaves vertex k fixed. There are two cases of reflection, depending on whether n
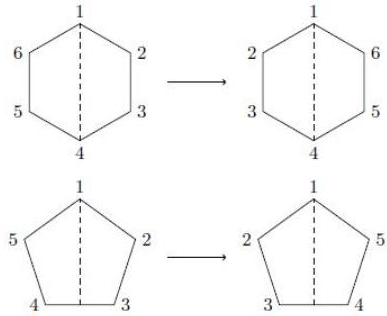 Types of reflections of a regular n-gon
Types of reflections of a regular n-gon
is even or odd. If there are an even number of vertices, then 2 vertices are left fixed by a reflection. If there are an odd number of vertices, then only a single vertex is left fixed by a reflection (Figure). In either case, the order of sk is two. Let s = s1. Then s2 = e and rn = e. Since any rigid motion t of the n-gon replaces the first vertex by the vertex k, the second vertex must be replaced by either k + 1 or by k - 1. If the second vertex is replaced by k + 1, then t = rk-1. If it is replaced by k - 1, then t = rk-1 s. Hence, r and s generate Dn; that is, Dn consists of all finite products of r and s. We will leave the proof that srs = r-1 as an exercise.
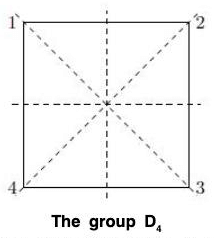
Example : The group of rigid motions of a square, D, consists of eight elements. With the vertices numbered 1, 2, 3, 4 (Figure), the rotations are
r = (1234)
r2 = (13)(24)
r3 = (1432)
r4 = e
and the reflections are
s1 = (24)
s2 = (13).
The order of D4 is 8. The remaining two elements are
rs1 = (12) (34).
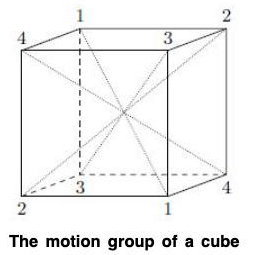
The Motion Group of a Cube
We can investigate the group of rigid motions as geometric objects other than a regular n-sided polygon to obtain interesting examples of permutation groups. Let us consider the group of rigid motions of a cube. A cube has 6 sides. If a particular side is facing upward, then there are four possible rotations of the cube that will preserve the upward-facting side. Hence, the order of the group is 6.4 = 24. We have just proved the following proposition.
Proposition : The group of rigid motions of a cube contains 24 elements.
Theorem : The group of rigid motions of a cube is S4.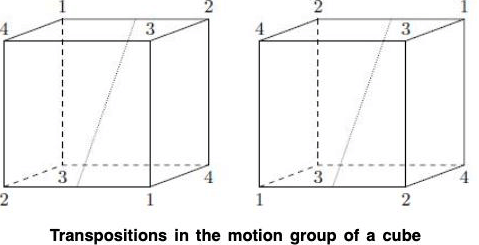
Proof : From Proposition, we already know that the motion group of the cube has 24 elements, the same number of elements as there are in S4. There are exactly four diagonals in the cube. If we label these diagonals 1, 2, 3, and 4, we must show that the motion group of the cube will give us any permutation of the diagonals (Figure). If we can obtain all of these permutations, then S4 and the group of rigid motions of the cube must be the same. To obtain a transposition we can rotate the cube 180° about the axis joining the midpoints of opposite edge (Figure). There are six such axes, giving all transpositions in S4. Since every element in S4 is the product of a finite number of transitions, the motion group of a cube must be S4.
Cosets
Coset of H is G
Let G be a group and H a subgroup of G. For any a ∈ G, the set {ah I h ∈ H} is denoted by aH. Analogously, Ha = {ha I h ∈ H} and aHa-1 = {aha-1 | h ∈ H}. When H is a subgroup of G, the set aH is called the left coset of H in G containing a whereas Ha is called the right coset of H in G containing a. In this case, the element a is called the coset representative of aH(or Ha). We use |aH| to denote the number of elements in the set aH, and |Ha| to denote the number of elements in Ha.
Remarks : 1. In general aH ≠ Ha but in an abelian group G, aH = Ha, ∀ a ∈ G
Sometimes the cosets (left and right) are equal even if the group is not abelian.
If the composition of the group G is addition (+), then aH and Ha are written as a + H and H + a respectively.
Example : Let G = (Z, +) and H = 2Z = {0, ±1, ± 2, ± 4, ...} then the right cosets of H in G are:
H + 0 = {0, ±2, ±4, ...,} = H
H + 1 = {0 + 1, ±2 + 1, ±4 + 1, ...}
H + 2 = {0 + 2, ±2 + 2, ±4 + 2, ...} = H etc.
It can be easily observed that any right coset and its corresponding left coset are equal i.e.,
H + 1 = 1 + H, H + 2 = 2 + H etc.
Again H + 3 = {..., - 6, - 3, - 1, 1, 3, 7, 9, ...} = H + 1
H + 4 = {..., - 5 , - 2 , 0, 2, 4, 6, 8, 10, ...} = H + 2 etc.
Similarly H + 5 = H + 1,H + 6 = H
and H + (-1) = H + 2, H + (-2) = H + 1 etc.
Thus H has only two distinct cosets H, H + 1 in Z.
Clearly, G = H ∪ (H + 1)
Example : If H = {1, - 1 } and G = [{1, - 1 , i, - i } , x] then different cosets of H in G are as follows:
1H = H1 = {1-1, -1-1} = {1, -1} = H
-1H = H(-1) = {1(-1), -1 (-1)} = {-1, 1} = H
iH = Hi = { 1 i , -1 -i} = { i , - i}
- iH = H (-i) = {1 *(-i). -1(-i)} = {-i, i)
Example : Klein’s 4 group :
The subgroup {e, a} of the group {e, a, b, c} has right cosets {e, a} and {b, c} which are left cosets also.
Similarly, cosets (right and left) of the subset {e, b} are {e, b} and {a, c} and {e, c} and {a, b} are cosets of the sub group {e, c}.
Properties of cosets
Theorem : If H is a subgroup of a group G and a ∈ G then :
a ∈ aH and a ∈ Ha
Proof. Let e be the identity element of G so also of H.
Then for every a ∈ G, e ∈ H ⇒ ae = a ∈ aH
and e ∈ H ⇒ ea = a ∈ Ha
Remark. From the above theorem, it is clear then
aH ≠ φ, Ha ≠ φ, ∀ a ∈ G
Theorem : If H is a subgroup of a group G, then G is equal to the union of all left (right) cosets of H, i.e.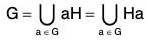
Proof : ∵ a ∈ G ⇒ a ∈ aH [by above Theorem]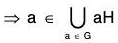 ...(1)
...(1)
Again since aH ⊂ G, V a ∈ G
∴ 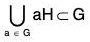 ...(2)
...(2)
(1) and (2) ⇒ G = 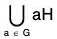
Similarly it can also be proved that 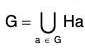
Theorem : If H is a subgroup of a group G, then for any a, b ∈ G :
(a) aH ∼ bH and Ha ∼ Hb
(b) aH ~ Ha
(A ~ B mean that there exist one to one correspondence between A and B)
Proof : (a) In order to establish one to one correspondence between aH and bH, we shall show that there exists one one onto mapping between aH and bH.
Define a mapping f from aH to bH as follows :
f : aH → bH, f(ah) = bh, ∀ b ∈ H
For h1, h2 ∈ H, we observe that
f(ah1) = f(ah2) ⇒ bh1 = bh2
⇒ h1 = h2 [by cancellation law in G]
⇒ ah1 = ah2
∴ f is one one.
Again x ∈ bH ⇒ H contains an element h such that x = bh
⇒ ah ∈ aH such that f(ah) = bh = x
∴ f is onto.
Therefore f is a bijection.
Consequently, aH ~ bH i.e., there is a one to one correspondence between any two left cosets of a H in G.
Similarly this can be proved that Ha ~ Hb also.
(b) Define a mapping f from aH to Ha as follows :
f : aH → Ha, f(ah) = ha, ∀ h ∈ H
For h1, h2 ∈ H, we have
f(ah1) = f(ah2) ⇒ h1a = h2a
⇒ h1 = h2 [by cancellation law in G]
⇒ ah1 = ah2
f is one one.
Again for each ha ∈ Ha, aH contains an element ah such that
f(ah) = ha
∴ f is onto.
which proves that aH ~ Ha.
Corollary 1. There is one to one correspondence between H and every left (right) coset of H.
H ~ aH, H ~ Ha, a ∈ G
i.e., there exist one to one correspondence between H and left (right) cosets of H.
Since H is a left and right coset of H itself, therefore by the above theorem
H ~ aH and H ~ Ha, ∀ a ∈ G
Corollary 2. If H is a finite subgroup of a group G, then :
O(aH) = O(H) = O(Ha), ∀ a ∈ G
The function from the set aH to the set bH given by ah ↦ bh is clearly onto. It is one-to-one since bh1 = bh2 ⇒ h1 = h2 ⇒ ah1 = ah2. So |aH| = |bH|.
Theorem : Any two left (right) cosets of a subgroup are either identical or disjoint.
Proof. Let H be a subgroup of a group G having two left cosets aH and bH which are not disjoint.
To Prove : aH = bH.
∵ aH ∩ bH = φ ⇒ there exist atleast one common element in bH and aH.
Let x ∈ aH and x ∈ bH, where x = ah1, x = bh2, h1, h2 ∈ H.
Now x = ah1 = bh2 ⇒ a = bh2h1-1 and b = ah1h2-2 ...(1)
Therefore for any h ∈ H
ah ∈ aH ⇒ ah = (bh2h1-1) h
= b(h2h1-1h) ∈ bH [∵ h2h1-1 h ∈ H]
∴ aH ⊂ bH ...(2)
Again bh ∈ bH ⇒ bh = (ah1h2-1)h
= a (h1h2-1h) ∈ aH [∵ h2h1-1 h ∈ H]
∴ bH ⊂ aH ...(3)
(2) and (3) ⇒ aH = bH
Therefore aH ∩ bH ≠ φ ⇒ aH = bH
i.e., any two left cosets of H are identical if they are not disjoint.
Similarly this property can also be proved for the right cosets.
Example : Let G = S3 and H = {(1), (13)}. Then the left cosets of H in G are:
(1) H = H,
(12) H = {(12), (12)(13)} = {(12), (132)} = (132)H,
(13) H = {(13), (1)} = H,
(23) H = {(23), (23)(13)} = {(23), (123)} = (123)H.
Lemma : Properties of Cosets
Let H be a subgroup of G, and let a and b belong to G. Then,
- a ∈ aH,
- aH = H if and only if a ∈ H,
- aH = bH or aH ∩ bH = θ,
- aH = bH if and only if a-1b ∈ H,
- |aH| = |bH|,
- aH = Ha if and only if H = aHa-1
- aH is a subgroup of G if and only if a ∈ H.
Lagrange's Theorem And Consequences
Theorem : Lagrange’s Theorem : |H| Divides |G|
If G is a finite group and H is a subgroup of G, then |H| divides |G|. Moreover, the number of distinct left (right) cosets of H in G is IGI/IH.
Or
For any finite group G, the order (number of elements) of every subgroup H of G divides the order of G.
Proof : Let a1H, a2H, .... arH denote the distinct left cosets of H in G. Then, for each a in G, we have aH = aiH for some i. Also, by property 1 of the lemma, a ∈ aH. Thus, each member of G belongs to one of the cosets aiH. In symbols, G = a1H ∪ ... ∪ arH.
Now, property 3 of the lemma shows that this union is disjoint, so that |G| = |a1H| + |a2H| + ... + |arH|.
Finally, since |aiH| = |H| for each i, we have |G| = r|H|.
Hence, the result follows.
OR
Proof : Suppose there are m cosets of H in G. Since G is the disjoint union of them and each coset has |H| elements, it follows that |G| = m.|H| and so |H| divides |G|.
Note : The converse of Lagrange’s Theorem is not true in general, it is true only for cyclic groups.
Corollary 1 : |a| Divides |G|
In a finite group, the order of each element of the group divides the order of the group:
Proof: Recall that the order of an element is the order of the subgroup generated by the element.
Corollary 2 : Group of Prime Order Are Cyclic
A group of prime order is cyclic.
Proof : Suppose that G has prime order. Let a ∈ G and a ≠ e. Then, |<a>| divides |G| and |<a>| ≠ 1. Thus, |<a>| = |G| and the corollary follows.
Corollary 3 : a|G| = e
Let G be a finite group, and let a ∈ G. Then, a|G| = e.
Proof : By Corollary 1, |G| = |a|k for some positive integer k.
Thus, a|G| = a|a|k = ek = e.
Corollary 4 : Fermat’s Little Theorem
Let p be a prime number, and a any integer. Then ap - a is always divisible by p. This can also be written as ap ≡ a (mod p).
Proof by induction:
First we will show that the theorem is true for all positive integers a by induction. The base case (when a = 1) is obviously true: 1P ≡ 1 (mod p).
By the binomial theorem,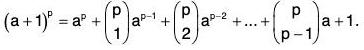
But 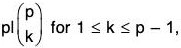 because p|p! but
because p|p! but 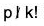 and
and 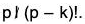 So the middle terms vanish mod p:
So the middle terms vanish mod p:
(a + 1)p = (ap + 1) (mod p).
Substituting ap ≡ a (mod p) by the inductive hypothesis gives (a + 1)p ≡ (a + 1) (mod p)
So the result holds for all positive a by induction. But every integer is congruent mod p to a positive integer, so the result holds for every integer.
Corollary 5 : Every group of prime order is cyclic
Proof : Let G be a group of order p, where p is prime.
Now O(G) = p prime ⇒ p > 1
⇒ G has atleast one element other than the identity.
Therefore let a ∈ G, a ≠ e. If H = [a], then
O(H) | O(G) [by Lagrange’s theorem]
⇒ O(H) | p
⇒ O(H) = p or O(H) = 1 [∵ p is prime]
⇒ O(H) = p = O(H) [∴ H ≠ {e}]
Similarly H ⊂ G and O(H) | O(G)
⇒ G = H = [a]
Therefore G is a cyclic group with its every element as generator except the identity.
Corollary 6. A group of prime order has no proper subgroup.
Proof. Let G be a group of order p, where p is prime.
If H a subgroup of G order m, then by Lagrange’s theorem m is a divisor of p. But p is prime, therefore m = p or 1.
Hence H = G or H = {e}
which are improper subgroup of G.
As such G has no proper subgroup.
Index of a subgroup. Definition :
Let H be a subgroup of a group G. Then the number of the distinct right (left) cosets of H in G, is known as the index of H in G.
This is denoted by [G : H].
If G is a finite group and H has k different left (right) cosets in G, then by the Lagrange’s theorem.
O(G) = k.O(H)
⇒ 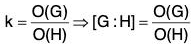
⇒ O(G) = O(G)[G:H]
For example, If H = {1, - 1} and G = [{1, - 1, i - i}, x], then [G : H] = 2 because the number of distinct cosets of H is 2.
Euler’s φ-function. Definition :
The Euler’s φ-function. φ(n), in defined for n ∈ N by
(1) φ (1) = 1
(2) For n > 1, φ(n) = the number of positive integers less than n and relatively prime to n.
Theorem Euler’s Theorem :
If n ∈ N and any integer a is relatively prime to n, then aφ(n) = 1 (mod n), where φ is an Euler φ- function.
Proof. For any integer x, let
[x] = Residue class of the set of integers mod n and G = {[a] : a is an integer relatively prime to n}
We know that residue class G is a group of order φ(n) wrt multiplication and its identity element is residue class [1].
Now [a] ∈ G ⇒ [a]o(G) = [1]
⇒ [a]φ(n) = [1]
⇒ [a][a][a]...(φ(n) times) = [1]
⇒ [a.a.a. ...(φ(n) times]) = [1]
⇒ [aφ(n)] = [1]
⇒ aφ(n) = 1 (mod n)
Theorem Fermat’s Theorem :
If p is a prime and a is any integer, then ap ≡ a (mod p)
Proof. Let G = ({[1], [2], [3],..., [p - 1]}, x p) = Set of non zero residue class of integers modulo p
If p is a prime number, then G is a group wrt multiplication of residue classes whose order is (p - 1) and identity element is [1].
Now let a be an integer.
Case I. p | a (p is a divisor of a)
a ≡ 0 (mod p) i.e., [a] = [0]
So [a] is not an element of G.
But p | a ⇒ p | ap ⇒ p | (ap - a)
⇒ ap ≡ a (mod p)
Case II. p 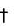 a (P is not a divisor of a) :
a (P is not a divisor of a) :
In this case [a] ≠ [0]
So [a] is an element of G.
Therefore [a]o(G) = [1] ⇒ [a]p-1 = [1]
⇒ [ ap-1] = [1]
⇒ ap-1 = 1 (mod p)
⇒ p | (ap-1 - 1)
⇒ p | a(ap-1 - 1)
⇒ p I (ap - a) ⇒ ap ≡ a(mod p)
Theorem : If H is a subgroup of a group G and a, b ∈ G, then :
(a) Ha = Hb ⇔ ab-1 ∈ H
(b) aH = bH ⇔ b-1 a ∈ H
Proof. (⇒) Let Ha = Hb, then
Ha = Hb ⇒ Hab-1 = Hbb-1
⇒ Hab-1 = He = H
⇒ ab-1 ∈ H [∵ ab-1 ∈ H(ab-1) = H]
Conversely : (⇐) Let ab-1 ∈ H
then ab-1 ∈ H ab-1 [∵ x ∈ Hx, ∀ x ∈ H]
∴ ab-1 ∈ H and ab-1 ∈ H ab-1
⇒ Hab-1 = H [∵ any two right cosets are either identical or disjoint]
⇒ Hab-1b = Hb
⇒ Ha = Hb
∴ Ha = Hb ⇔ ab-1 ∈ H
Similarly (b) can also be proved.
Corollary : (a) Ha = H ⇔ a ∈ H
(b) aH = H ⇔ a ∈ H
Proof. (a) Let Ha = H, then
Ha = H ⇒ Ha = He
⇒ ae-1 ∈ H [by the above theorem]
⇒ a ∈ H
Again a ∈ H ⇒ ae-1 ∈ H
⇒ Ha = He [by the above theorem]
∴ Ha = H ⇔ a ∈ H
Similarly (b) can also be proved.
Relation of congruence modulo w.r.t. a subgroup in a group
Let H be a subgroup of a group G and a, b ∈ G, then a is said to be “congruent mod H”, to b if ab-1 ∈ H.
It is denoted by a = b(mod H)
Theorem : The relation of congruency in a group G, defined below, is an equivalent relation, where H is a subgroup of G:
a ≡ b(mod H) ⇔ ab-1 ∈ H
Proof : (i) Reflexive : Let a ∈ G, then
aa-1 = e ∈ H ⇒ a ≡ a(mod H)
∴ the relation is reflexive.
(ii) Symmetric : Let a ≡ b (mod H). then
a ≡ b (mod H) ⇒ ab-1 ∈ H
⇒ (ab-1)-1 i H [∵ H is a subgroup]
⇒ ba-1 ∈ H
⇒ b ≡ a (mod H).
∴ the relation is symmetric.
(iii) Transitive : Let a = b (mod H) and b ≡ c (mod H). then a ≡ b(mod H), b ≡ c(mod H) ⇒ ab-1 ∈ H and bc-1 ∈ H
⇒ (ab-1)(bc-1) ∈ H
⇒ a(b-1b)c-1 ∈ H
⇒ ac-1 ∈ H
⇒ a ≡ c(mod H)
Therefore the relation is transitive.
Therefore the above congruence relation defined in G is an equivalence relation.
As such this partitions G into mutually disjoint equivalence classes.
We now show that corresponding to the equivalence class of any a ∈ G i.e., C(a) = {x ∈ G | x ≡ a (mod H)} is some as right coset Ha, because
x ∈ C(a) ⇒ x ≡ a (mod H) ⇒ xa-1 ∈ H
⇒ xa-1 a ∈ Ha ⇒ x ∈ Ha
∴ C(a) ⊂ Ha ...(1)
and x ∈ Ha ⇒ xa-1 ∈ Haa-1 = H
⇒ x ≡ a (mod H ) ⇒ x ∈ C(a)
Ha ⊂ C(a) ...(2)
(1) and (2) ⇒ C(a) = Ha, ∀ a ∈ G
Remark. Similarly it can also be proved that the relation in G defined by a ≡ b (mod H) ⇔ a-1 b ∈ H is also an equivalence relation which partitions the group G into mutually disjoint equivalence classes wrt H. In this case the equivalence class c(a) corresponding to a ∈ G is the left coset aH corresponding to a.
Example : Find all the cosets of 3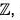 in the group (
in the group (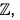 , +).
, +).
Let H = 3
= {..., 6, -3, 0, 3, 6, ...}.
The following distinct cosets of H in G are obtained :
0+ H = H + 0= {..., -6, -3, 0, 3, 6, ...} = H
1 + H = H + 1 = {..., -5, -2, 1, 4, 7, ...}
2 + H = H + 2 = {..., -4, -1, 2, 5, 8, ...}
3 + H = H + 3 = {..., -3, 0, 3, 6, 9, ...} = H + 0
4 + H = H + 4 = {..., -2, 1, 4, 7, 10, ...} = H + 1
5 + H = H + 5 = {..., -1, 2, 5, 8, 11, ...} = H + 2
6 + H = H + 6 = {..., 0, 3, 6, 9, ...} = H + 0
-1 + H = H + (-1) = {..., -7, -4, -1, 2, 5, ...} = H + 2
-2 + H = H + (-2) = {..., -8, -5, -2, 1, 4, ...} = H + 1
-3 + H = H + (-3) = {..., -9, -6, -3, 0, 3, ...} = H + 0
On observing the above cosets, it is clear that
H + 0 = H + 3 = H + 6 = H + 9 . . . = H + (-3) = H + (-6)...
H + 1 = H + 4 = H + 7 = H +10 . . . = H + (-2) = H + (-5)...
H + 2 = H + 5 = H + 8 = H + 11 ... = H + (-1) = H + (-4)...
Therefore three cosets of H in G are the following :
H, H + 1, H + 2Remark : There are n cosets of
Example : Find all the cosets of H = {0, 4} in the group G = 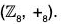
Here G = {0, 1, 2, 3, 4, 5, 6, 7} and H = {0, 4}, G
The following distinct cosets of H in G are obtained :
0 + H = H + 0 = {0, 4} = H
1 + H = H + 1 = {0 +8 1, 4 +8 1} = {1, 5}
2 + H = H + 2 = { 0 +8 2, 4 +8 2} = {2, 6}
3 + H = H + 3 = {0 +8 3, 4 +8 3} = {3, 7}
4 + H = H + 4 = {0 +8 4, 4 +8 H} = {4, 0} = H
5 + H = H + 5 = {0 +8 5, 4 +8 5} = {5, 1} = H + 1
6 + H = H + 6 = {0 +8 6, 4 +8 6} = {6, 2} = H + 2
7 + H = H + 7 = {0 +8 7, 4 +8 7} = {7, 2} = H + 3
On observing the above cosets, it is clear that four coset of H in G are :
H, H + 1, H + 2, H + 3.
Example : If H is a subgroup of a group G, then prove that T = {x ∈ G I xH = Hx} is a subgroup of G.
∵ e ∈ G ⇒ eH = H = He ⇒ e ∈ T ⇒ T ≠ Φ
∴ Let x1, x2, ∈ T; then by the definition of T,
x1H = Hx1 and x2H = Hx2
then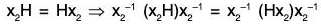
Again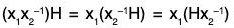
[∵ x2 ∈ T]
= H(x1x2-1)
∴ x1x2-1 ∈ T
Similarly x1 ∈ T, x2 ∈ T ⇒ x1x2-1 ∈ T
∴ T is a sub group of G.
Example : If H is a subgroup of a group G and g ∈ G, then prove that :
(a) gHg-1 = {ghg-1 | h ∈ H} is a subgroup of G.
(b) If H is finite, then O(H) = O(gHg-1).
(a) Let x = gh1g-1 ∈ gHg-1
and y = gh2g-1 ∈ gHg-1 where h1h2 ∈ H
then xy-1 = (gh1g-1)(gh2g-1)-1
= (gh1g-1)(g-1)-1, h2-1g-11
= (gh1g-1)(gh2-1g-1)
= gh1(g-1g)h2-1g-1 [by associativity]
= gh1eh2-1g-1
= g(h1h2-1)g-1 ∈ gHg-1 [∵ h1h2-1 ∈ H]
Similarly x ∈ gHg-1, y ∈ gHg-1 ⇒ xy-1 ∈ gHg-1
∴ gHg-1 is a subgroup of G.
(b) Define a map f from H to gHg-1 as follows :
f : H → gHg-1, f(h) = ghg-1, ∀ h ∈ H.
∵ f(h1) = f(h2) ⇒ gh1g-1 = gh2g-1
⇒ h1 = h2 [by cancellation law]
∴ f is one one.
Again for every ghg-1 ∈ gHg-1, there exist h ∈ H such that
f(h) = ghg-1
∴ f is onto.
Hence f is a bijection which proves that O(H) = O(gHg-1).
Example : If H and K are two finite subgroups of a group G such that H ⊂ K then prove that : [G : H] = [G : K] [K : H]
Let H and K be two subgroups of a group G and H ⊂ K,
∴ H is also a subgroup of K.
Now by definition of index of a subgroup in a group.
[G:H] = O(G)/O(H) ...(1)
[G:H] = O(G)/O(K) ...(2)
[K:H] = O(K)/O(H) ...(3)
From (2) and (3),
= [G : H] [by (1)]
Example : If H is a subgroup of a group G with index 2 i.e., I G : H I = 2, then prove that aH = Ha, ∀ a ∈ G.
Since H is a subgroup of index 2 of a group G, therefore the number of distinct left (right) cosets of H in G is 2.
Since H itself is a left and right coset, therefore let
G = H ∪ Ha, where H ∩ Ha = φ ...(1)
Again if H and bH are two disjoint left cosets, then
G = H ∪ bH ...(2)
From (1) and (2), G = H ∪ Ha = H ∪ bH
⇒ G - H = Ha = bH [∵ H ∩ Ha = F = H ∩ bH]
Now ∵ a ∈ Ha
∴ a ∈ Ha, Ha = bH ⇒ a ∈ bH
⇒ bH = aH [∵ a ∈ aH]
∴ Ha = bH = aH
∴ Ha = aH, ∀ a ∈ G
Example : If H and K are two finite subgroups of an abelian group G, then prove that :
O(HK) = 
Let D = H ∩ K and Dk1, Dk2,..., DKi
be all the distinct right cosets of D in K. Therefore...(1)
Now[∵ D ⊂ H ⇒ HD = H] ...(2)
Again we see that any two cosets of Hk1, Hk2, .... Hkt are pairwise disjoint because
Hki = Hkj ⇒ ki . kj-1 ∈ H
⇒ kj. kj-1 ∈ H ∩ K = D [∵ kikj-1 ∈ K]
⇒ Dki = Dkj
which is a contradiction to our supposition. Thus Hk1, Hk2...... Hki are all distinct.
Therefore by (2)
O(HK) = O(Hk1) + O(Hk2) + ... + O(HKi)
= t . O(H) [∵ O(Hki) = O(H), ∀ i][by (1)]
Example : If H is a subgroup of a group G and a ∈ G, then prove that :
(Ha)-1 = a-1H
Let ha ∈ Ha, where h ∈ H then (ha)-1 ∈ (Ha)-1,
but (ha)-1 = a-1h-1 ∈ a-1 H [∵ h ∈ H ⇒ h-1 ∈ H]
(Ha)-1 ⊂ a-1 H ...(1)
Again if a-1 h ∈ a-1 H, then
a-1h = a-1(h-1)-1 = (h-1a)-1 ∈ (Ha)-1 [∵ h-1 ∈ H]
∴ a-1 H ⊂ (Ha)-1
From (1) and (2), (Ha)-1 = a-1H
Example : If H is a subgroup of a group G, then show that any two right cosets Ha and Hb are distinct iff left cosets a-1 H and b-1 H are distinct.
If possible, let Ha and Hb be the two right cosets of H in G when left cosets a-1H and b-1H are equal, then
a-1H = b-1H ⇒ (b-1)-1 a-1 ∈ H [∵ aH = bH ⇒ b-1 a ∈ H]
⇒ a-1b ∈ H
⇒ (ba-1)-1 ∈ H [∵ H is a sub group]
⇒ (a-1)-1 b-1 ∈ H ⇒ ab-1 ∈ H
⇒ Ha = Hb [∵ ab-1 ∈ H ⇒ Ha = Hb]
which is a contradiction. Therefore
Ha ≠ Hb ⇒ a-1 H ≠ b-1 H
Conversely, it can also be proved that
a-1H ≠ b-1H ⇒ Ha ≠ Hb
Therefore Ha ≠ Hb ⇔ a-1H1b-1H.
|
98 videos|34 docs|32 tests
|
FAQs on Group Theory- III - Mathematics for Competitive Exams
| 1. What is a permutation in group theory? |  |
| 2. What is the Dihedral Group in group theory? |  |
| 3. What are cosets in group theory? |  |
| 4. What is Lagrange's Theorem in group theory? |  |
| 5. What are some consequences of Lagrange's Theorem in group theory? |  |