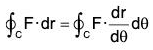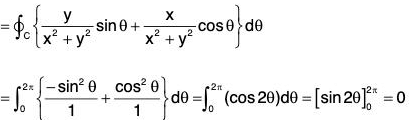Vector Calculus - (Part - 1) | Mathematics for Competitive Exams PDF Download
| Table of contents |

|
| Scalar and Vector |

|
| Gradient of A Scalar Point Function |

|
| Divergence of A Vector Point Function |

|
| Curl of a Vector Point Function |

|
| Line Integral |

|
Scalar and Vector
A VECTOR is a quantity having both magnitude and direction, such as displacement, velocity, force, and acceleration.
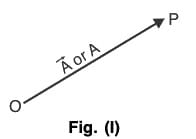
Graphically a vector is represented by an arrow OP (Fig.I) defining the direction, the magnitude of the vector being indicated by the length of the arrow. The tail end O of the arrow is called the origin or initial point of the vector, and the head P is called the terminal point or terminus.
Analytically, a vector is represented by a letter with an arrow over it, as A in Fig. (I) and its magnitude is denoted by 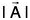 or A. In printed works, bold faced type, such as A, is used to indicate the vector
or A. In printed works, bold faced type, such as A, is used to indicate the vector 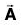 while IAI or A indicates its magnitude. The vector OP is also indicated as
while IAI or A indicates its magnitude. The vector OP is also indicated as 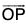 or OP; in such case we shall denote its magnitude by
or OP; in such case we shall denote its magnitude by 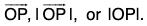
 A SCALAR is a quantity having magnitude but no direction, e.g. mass, length, time, temperature, and any real number. Scalars are indicated by letters in ordinary type as in elementary algebra. Operations with scalars follows the same rules as in elementary algebra.
A SCALAR is a quantity having magnitude but no direction, e.g. mass, length, time, temperature, and any real number. Scalars are indicated by letters in ordinary type as in elementary algebra. Operations with scalars follows the same rules as in elementary algebra.
Vector Algebra
The operations of addition, subtraction and multiplication of scalars of vectors.
- The vectors A and B are equal if they have the same magnitude and direction regardless of the position of their initial points. Thus A = B in Fig. (II)
- A vector having direction opposite to that of vector A but having the same magnitude is denoted by - A Fig. (Ill)

- The sum or resultant of vectors A and B is a vector C formed by placing the initial point of B on the terminal point of A and then joining the initial point of A to the terminal point of B. This sum is written A + B, i.e. C = A + B.
- The difference of vectors A and B, represented by A - B, is that vector C which added to B yields vector A. Equivalently, A - B can be defined as the sum A + (-B).
- The product of a vector A by a scalar m is a vector mA with magnitude Iml times the magnitude of A and with direction the same as or opposite to that of A, according as m is positive or negative. If m = 0, mA is the null vector.
Laws of Vector Algebra
If A, B and C are vectors and m and n are scalars, then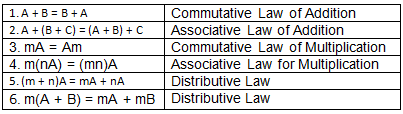
A UNIT VECTOR is a vector having unit magnitude, If A is a vector with magnitude A ≠ 0, then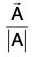 is a unit vector having the same direction as A.
is a unit vector having the same direction as A.
The Rectangular Unit Vector i, j, k
An important set of unit vectors are those having the directions of the positive x, y, and z axes of a three dimensional rectangular coordinate system, and are denoted respectively by i, j, and k Fig. (IV).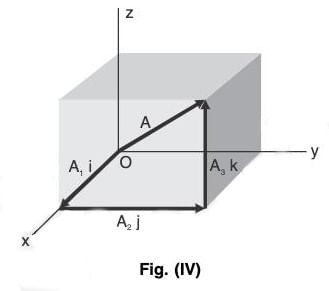
Components of a Vector
Any vector A in 3 dimensions with initial point at the origin O of a rectangular coordinate system Fig. (IV). Let (A1, A2, A3) be the rectangular coordinates of the terminal point of vector A with initial point at O. The vectors A1i, A2j, and A3k are called the rectangular component vectors or simply component vectors of A is the x, y and z directions respectively. A1, A2 and A3 are called the rectangular components or simply components of A in the x, y and z directions respectively.
The sum or resultant of A2i, A2j and A3k is the vector A so that we can write
A = A1i + A2j + A3k
The magnitude of A is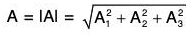
In particular, the position vector or radius vector r from O to the point (x, y, z) is written as r = xi + yj + zk and the magnitude 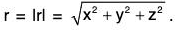
Scalar and Vector Point Functions Related to Field
(a) Scalar Field: If to each point (x, y, z) of a region R in space there corresponds a number or scalar ϕn (x, y, z), then n is called a scalar function of position or scalar point function and we say that a scalar field n has been defined in R.
A scalar field which is independent of time is called a stationary or steady state scalar field.
Examples:
- n(x, y, z) = x3y - z2 defines a scalar field.
- The temperature at any point within or on the earth’s surface at a certain time defines a scalar field.
(b) Vector Field: If to each point (x, y, z) of a region R in space there corresponds a vector 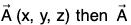 is called a vector function of position or vector point function and we say that a vector field A has been defined in R.
is called a vector function of position or vector point function and we say that a vector field A has been defined in R.
A vector field which is independent of time is called stationary or steady state vector field.
Examples :
 is a vector field.
is a vector field.- If the velocity at any point (x, y, z) within a moving fluid is known at a certain time, it is said to be a vector field.
Vector Function of A Single Scalar Variable
Scalar Function
Let i be the set of real numbers and D ⊂ j .
If corresponding to every t ∈ D, ϕ(t) is a unique scalar quantity, then ϕ(t) is called a scalar function of the variable t.
Vector Function: If corresponding to every t ∈ D, f(t) is a unique vector quantity, then f(t) is called a vector function of the variable t. If for every single value of t, f(t) has a unique value, then this is called a single valued vector function.
Every vector can be expressed as a Linear Combination [LC] of given three non-coplanar vectors.
Therefore f(t) can be expressed in the following decompose form
f(t) = f1(t)i + f2(t)j + f3(t)k,
where f1(t), f2(t), f3(t) are scalar functions of scalar variable t.
When a vector function r = f(t) is expressed in the component form, then that represents the position vectors of different points in space for different values of t(which is called the parameter). As t changes, the end point of r = f(t) determines a continuous curve which is called space curve.
Example: Let P be the position of a moving particle at any instant t along a curve whose position vector is r wrt the origin O. As the particle moves, the vector r also changes. Therefore r can be taken as the vector function of the time t.
Thus velocity and acceleration of a moving point are vector function of time t.
Conversely: A curve can always be represented in terms of position vector r of a point situated on it, where r is a function of scalar variable t (parameter).
Example: Standard Vector Equation of a Circle
We know that the parametric co-ordinates of any point on the circle with centre at the origin and radius a are
x = a cos t, y = a sin t ...(1)
Therefore, substituting from (1) in r = xi + yj + zk, the required standard vector equation is r = (a cos t)i + (a sin t)j + (0)k, where a is a constant and t is a scalar.
Example: Standard Vector Equation of Parabola : r = (at2)i + (2at)j + (0)k, where a is a constant.
Example: Standard Vector Equation of Ellipse :
r = (a cos t)i + (b sin t)j + (0)k,
where a and b are constant.
Limit of a Vector Function
Definition: A vector function f(t) is said to tend to a vector l called its limit, when t tends to t0, if given any number ε (however small) > 0, there corresponds a number δ > 0 such that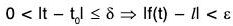
Thus if the limit of f(t) is l when t tends to t0, then this can be symbolically expressed in the form: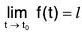
Some Theorems on Limits
Following are some of the theorem on limits of vector functions:
If f(t) and g(t) are two vector functions of a scalar variable t and ϕ(t) is scalar function of t, then: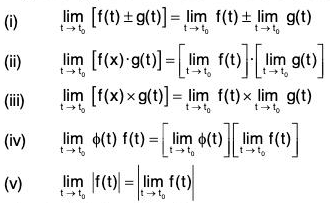
Continuity of a Vector Function
Definition: Any vector function f(t) is said to be continuous at t = t0, if corresponding to every positive quantity ε (however small), there exists a positive quantity δ such that
It - t0l < δ ⇒ lf(t) - f (t0)l < ε.
Clearly, the vector function f(t) is continuous at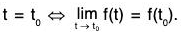
Derivative of a Vector Function
Let r = f(t) be a single valued continuous function of scalar variable t. Let δt be the arbitrary small increase in t and δr be the corresponding increase in r, i.e. δr = f(t + δt) - f(t)
If the limiting value of the ratio δr/δt when δt → 0 exist, then this is called the Derivative or Differential coefficient of r wrt t and is expressed by dr/dt.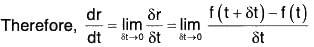
For any vector r = f(t) if dr/dt exist, then this called differentiable or derivable vector.
Geometrical interpretation of the derivative of a Vector Function:
Let r = f(t) be a single valued continuous function of scalar variable t which represent a curve in the space. Let r and r + δr be the values of this function corresponding to t and t + δt which represent the position vectors  of two neighbouring points P and Q.
of two neighbouring points P and Q.
Therefore r = f(t) = 
and r + δr = f(t + δt) = 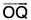
δr = (r + δr)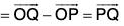
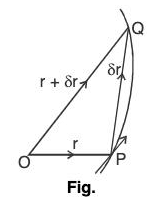
Hence δr/δt is a vector parallel to the vector 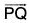 whose magnitude is 1/δt times the magnitude of δr. When δt → 0, then δr → 0 and in that case the direction of the vector
whose magnitude is 1/δt times the magnitude of δr. When δt → 0, then δr → 0 and in that case the direction of the vector 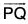 is along the direction of the tangent at the point P. Therefore the limiting value of δr/δt when δt → 0 i.e. dr/dt is a vector whose direction is along the tangent to r = f(t) at the point P.
is along the direction of the tangent at the point P. Therefore the limiting value of δr/δt when δt → 0 i.e. dr/dt is a vector whose direction is along the tangent to r = f(t) at the point P.
Successive Derivatives
If dr/dt is again differentiable wrt t, then its derivative is denoted by d2r/dt2 which is called the second derivative of r. Similarly, if d3r/dt3 exist, then this is called the third derivative of r etc. These are all called the successive derivatives of r and denoted by 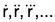 respectively.
respectively.
Derivative of a vector in terms of its components
Let r = xi + yj + zk, where x, y, z are any functions of the scalar variable t. Corresponding to the small arbitrary increase δt in t, there are increments δx, δy, δz and x, y, z and r respectively. Then
r + δr = (x + δx)i + (y + δy)j + (z + δz)k
⇒ δr = {(xi + yj + zk) + (δxi + δyj + δzk)} - r
⇒ δr = δxi + δyj + δzk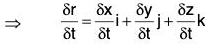
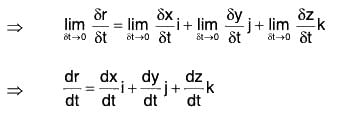
Constant Vector
Definition: A vector having constant magnitude and direction is called a constant vector.
Note: This may be clear that any vector is not a constant vector if only either magnitude or the direction is constant.
Derivative of a constant vector
Let r = c be a constant vector function of the scalar variable t. Therefore c is a constant vector,
∴ r + δr = c ⇒ dr = c - c = 0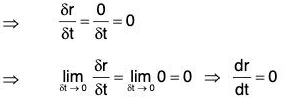
Therefore the derivative of a constant vector is zero vector (0).
Differentiation formulae for vectors
If a, b and c are differentiable vector functions of the same scalar variable t and ϕ is a scalar function of t, then:
(i) Derivative of the Sum and Difference of two vector functions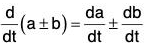
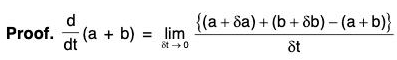
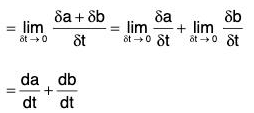
Similarly, it can be proved that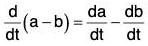
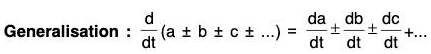
(ii) Derivative of a scalar Multiple of a vector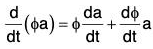
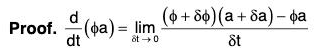

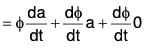 [∴ δt → 0 ⇒ δa ⇒ 0]
[∴ δt → 0 ⇒ δa ⇒ 0]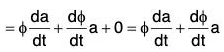
(iii) Derivative of the Dot Product of two vectors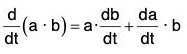
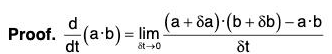
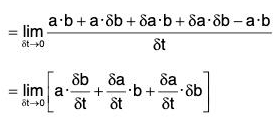
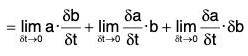
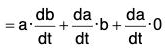 [∵ δt → 0 ⇒ δb → 0]
[∵ δt → 0 ⇒ δb → 0]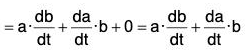
(iv) Derivative of Cross Product of two vectors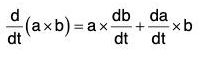
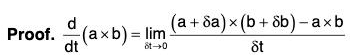

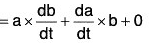 [∵ δt → 0 ⇒ δb → 0]
[∵ δt → 0 ⇒ δb → 0]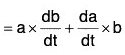
(v) Derivative of Scalar Triple Product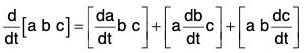
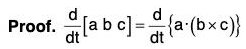 [by the notation of Scalar Triple Product]
[by the notation of Scalar Triple Product]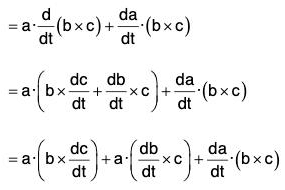
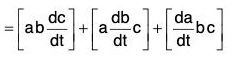 [by notation]
[by notation]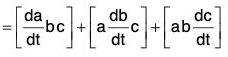 [in the cyclic order]
[in the cyclic order]
(vi) Derivative of Vector Triple Product 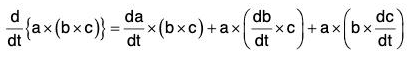
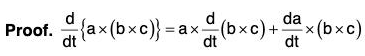
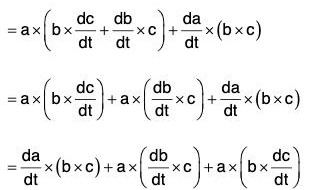
Derivative of the Function of a Function
Let r be a derivable function of scalar variable s and s be a derivable scalar function of scalar variable t.
Corresponding to a small increase δt in t, let δs and δr be the increase in s and r respectively, then
δt → 0 ⇒ δs → 0 and δr → 0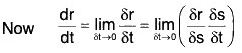
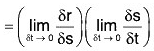
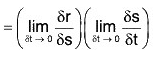 [δt → 0 ⇒ δs → 0]
[δt → 0 ⇒ δs → 0]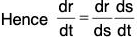
Some Important
Theorems Theorem: If a is a differentiable vector function of a scalar variable t and lal = a; then :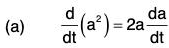
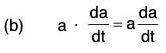
Proof, (a) ∵ a2 = a · a = |a||a| cos 0 = a2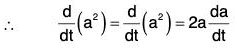
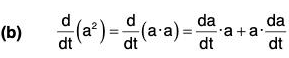
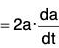
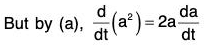
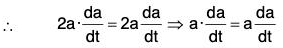
Theorem: The necessary and sufficient condition for any vector a(t) to be a constant vector is that da/dt = 0.
Proof. The condition is necessary (⇒) :
Let a(t) be a constant vector function of scalar variable t, then it will be proved that da/dt = 0
∵ a(t) is a constant function, therefore a(t + δt) = a(t)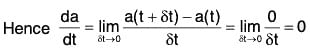
Therefore the condition is necessary i.e. the derivative of a constant vector is zero vector.
The condition of sufficient (⇐) :
Let da/dt = 0, then it will be proved that a is constant vector.
Let a(t) = a1(t)i + a2(t)j + a3(t)k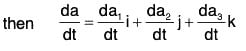
Therefore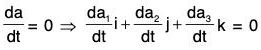
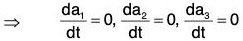
⇒ a1, a2, a3 are constant vectors independent of t.
⇒ a(t) is a constant vector.
Therefore, the condition is sufficient i.e. da/dt = 0
⇒ a is a constant vector.
Hence a(t) is a constant vector ⇔ da/dt = 0
Theorem : The derivative of a vector of constant magnitude is perpendicular to that vector provided the vector itself is not a constant vector.
Proof. Let a be a vector of constant magnitude but it is not a constant vector i.e., lal = a (constant) and da/dt ≠ 0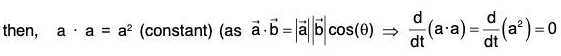
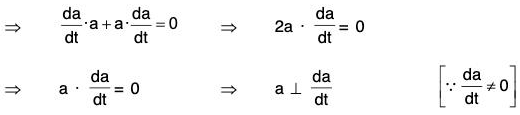
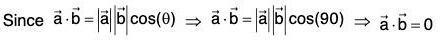
Therefore the derivative of a is perpendicular to a.
Theorem : The necessary and sufficient condition that a(t) is a vector of constant magnitude is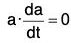
Proof. The condition is necessary (⇒) :
Let the magnitude of the vector a(t) is constant i.e., lal = a (constant)
Then a · a = a2 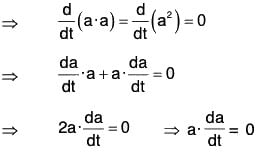
Therefore the given conditional is necessary.
The condition is sufficient (⇐) :
Let a(t) be a vector such that 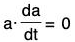
Then it will be proved that the magnitude of a will be constant,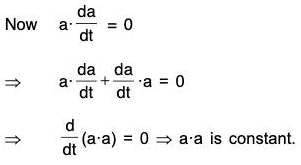
⇒ a2 is constant lal is constant.
Therefore, the given condition is sufficient.
Hence la(t)l is constant 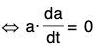
Theorem: The necessary and sufficient condition for the vector a(t) to have constant direction is 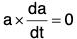
Proof. First we prove a lemma
Let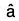 be unit vector along a and its magnitude be a, then by definition,
be unit vector along a and its magnitude be a, then by definition,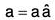
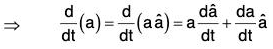 ....(1)
....(1)
Multiplying both sides of (1) vectorially by vector a,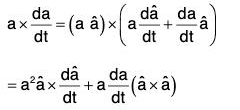
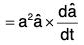
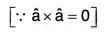 ....(2)
....(2)
The condition is necessary (⇒) :
Let the direction of the vector a(t) be constant. Then â will be a constant vector because its magnitude is 1 (constant).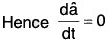
Therefore in this case, from (2)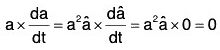
which shows that the given condition is necessary.
The condition is sufficient (⇐) :
Let a(t) be a vector such that 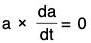 ....(3)
....(3)
then we shall prove that the direction of a is constant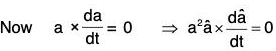 [by (2)]
[by (2)]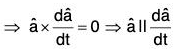 ...(4)
...(4)
Again the magnitude of â is 1.(constant).
Therefore by theorem,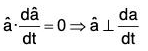 ....(5)
....(5)
(4) and (5) show that the vectors 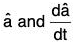 are mutually parallel as well as perpendicular (contradiction), which is possible only when
are mutually parallel as well as perpendicular (contradiction), which is possible only when 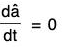
Since â ≠ 0, â will be a constant vector, being 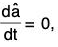
i.e., its direction will also be constant.
Consequently the direction of a(t) will also be constant.
Therefore the condition is sufficient.
Hence the direction of a(t) is constant 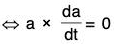
Unit tangent vector to a curve at a point
If r = f(t) is a single valued continuous and differentiable function of a scalar variable t, then we have seen that dr/dt is a vector whose direction is along the tangent at the point ‘t’ to the curve r = f(t).
Therefore, at the point‘t’
Tangential unit vector 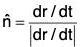
Instantaneous Velocity and Acceleration:
If t is the time and 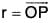 is the position vector of any moving point P wrt the origin O for the vector r = f(t), then δr = displacement of the particle in the interval δt
is the position vector of any moving point P wrt the origin O for the vector r = f(t), then δr = displacement of the particle in the interval δt
∴ δr/δt = average velocity of the particle in the interval δt
Hence if the velocity vector of any particle at the point P is v,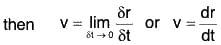 ....(1)
....(1)
Since the direction of the vector dr/dt is along the tangent at P on the curve, therefore the direction of the velocity of the particle at P will also be along the tangent at P on the curve.
Again if δv be the change in the velocity v of the particle in the time interval δt, then
δv/δt = average acceleration of the particle in the interval δt
Hence if the acceleration vector of any particle at the point P is f,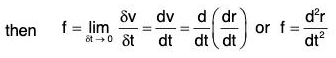 ...(2)
...(2)
Example : If r = a cos t i + a sin t j + t k, find the following:
(a) dr/dt
(b) |dr/dt|
(c) d2r/dt2
(d) |d2r/dt2|
(a) Given r = a cos t i + a sin t j + t k
= -a cos t i - a sin t j + 0k
= -a (cos t i + sin t j)
Partial Derivatives of Vectors
Let r = f(x , y, z ,....) be a vector function of independent variables x, y, z , ...... Let δr be the change in r due to the small change δx in x, whereas there is no change in other independent variables, then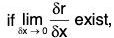 is called the partial derivative of the vector r wrt x and is denoted by ∂r/∂x.
is called the partial derivative of the vector r wrt x and is denoted by ∂r/∂x.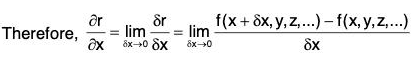
Clearly ∂r/∂x is the ordinary differential coefficient or derivative of r wrt x and all other independent variables are treated as constants.
Similarly, the partial derivatives of r wrt other independent variables y, z, ... etc. can also be defined and denoted respectively by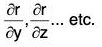
Successive partial derivatives of a vector function r can also be defined as in calculus of scalar variables: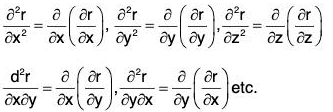
If second order partial derivative of r are continuous, then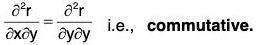
If a and b are two vector functions of independent variables x, y, z and ϕ is a scalar function of x, y, z, then the following results can be easily proved:
where a1, a2, a3 are scalar functions of independent variables x, y, z.
Example 1: If r = (2x2y - x4)i - (exy - y sin x)j + (x2 cos y)k, find the following:
(a) ∂r/∂x
(b) ∂r/∂y
(c) ∂2r/∂x2
(d) ∂2r/∂y2
(e) ∂2r/∂x∂y
(f) ∂2r/∂y∂x
Also show that : ∂2r/∂x∂y = ∂2r/∂y∂x
∵ r = (2x2y - x4)i - (exy - y sin x)j + (x2 cos y) k
= (4xy - 4x3)i - (yexy - y cos x)j + (2x cos y)k ....(1)
Similarly,
= (2x2) i - (xexy - sin x) j - (x2 sin y)k ....(2)[by (1)]
= (4y - 12x2) i - (y2exy + y sin x) j + (2 cos y)k ....(3)[by (2)]
= - x2 exy j - x2 cos yk .....(4)[by (2)]
= 4xi - (exy + xyexy - cos x)j - 2x sin yk ....(5)[by (1)]
= 4 xi - (exy + xyexy - cos x)j - 2x sin yk ....(6)
From (5) and (6), the required result is verified.
Example 2: If a = x2yz i - 2xz3 j + xz2 k; b = 2zi + yj - x2k ;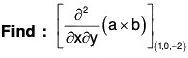
....(1)
or first calculate a x b by
if a = a1i + a2 J + a3k
b = b1i + b2J + b3k
then first differentiate (a x b) by x and then by y.....(2)
....(3)
....(4)
Substituting the values from (2), (3), (4), (5) in (1),
= -z2i + 4x3z j + 4xyz k
∴ At the point (1, 0, - 2),
The Vector Differential Operator : [Del (∇)]
The vector operator ∇ is defined as follows: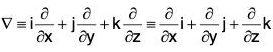
This is a differential operator which is read as *Del or ‘ Nabla
Scalar Point Function:
Let R be a region of points in the space. If a scalar quantity ϕ(P) or ϕ(x, y, z) is obtained corresponding to every point P(x, y, z) by some rule, then ϕ is called a scalar point function in the region R.
Example: The quantity of any thing.
Example: Density Example : Temperature (at any instant).
Scalar Field: The set of points in any region R and the vector function 4> at those points together is called a scalar field.
Example: Temperature distribution in any medium.
Example: Gravitational potential of a system of masses.
Example: Electrostatic potential of charges of a system.
Vector Point Function: Let R be a region of points in the space. If a scalar quantity V(P) or V(x, y, z) is obtained corresponding to every point P(x, y, z) by some rule, then V is called a vector point function in the region R.
Example: Velocity of any moving point of fluid at any instant.
Example: Force of electrical or magnetic intensity of any point of the electrical or magnetic field.
Vector Field: A vector field is a vector each of whose components is a scalar field, that is, a function of our variables. We use any of the following notations for one:
v(x, y, z) = (v1(x, y, z), v2(x, y, z), v3(x, y, z))
v(x, y, z) = v1(x, y, z)i + v2(x, y, z)j + v3(x, y, z)k
Example: Velocity of moving fluid at any instant
Example: Force of electricity intensity
Example: Force of magnetic intensity.
Gradient of A Scalar Point Function
Definition : If f(x, y, z) is a continuous differentiable scalar point function at every point (x, y, z), then gradient of f is expressed as grad f and defined as follows: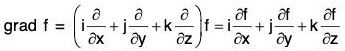 ...(1)
...(1)
The operation ∇ : Definition: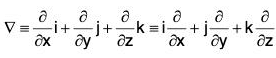 ....(2)
....(2)
This operator is called *Del or Nabla.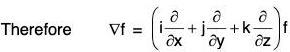 ...(3)
...(3)
∴ grad f = ∇f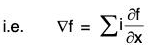
By the definition, it is clear that the gradient of any scalar point function f i.e. grad f is a vector whose components parallel to the co-ordinate axes are respectively 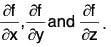
Theorems on Gradient
Theorem:
If f and g are scalar point function, then :
(a) grad (f ± g) = grad f ± grad g
(b) grad (f g) = f(grad g) + g(grad f)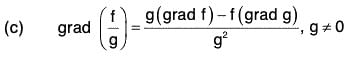
Proof, (a) grad(f ± g) = 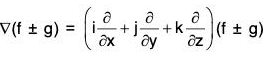
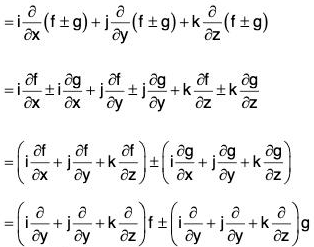
= grad f ± grad g
∴ ∇(f ± g) = ∇f ± Vg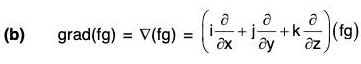
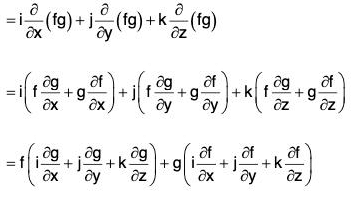
= f(grad g) + g(grad f)
∴ ∇(fg) = f(∇g) + g(∇f)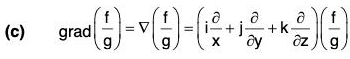
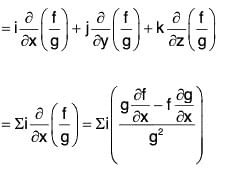
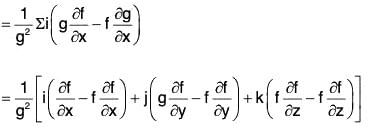
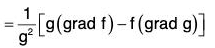
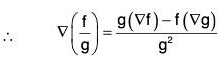
Gradient as Surface Normal Vector
The family of the surface given by f(x, y, z) = c with various values of c are called the level surfaces of the scalar function f. These surfaces are also called equipotential or iso surfaces e.g. isothermal surfaces.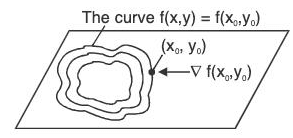 The gradient of a differentiable function of two variable at a point is always normal to the function’s level curve through that point.
The gradient of a differentiable function of two variable at a point is always normal to the function’s level curve through that point.
Let 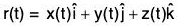 be a smooth curve on the level surface f(x, y, z) = c of a differentiable function f. Then
be a smooth curve on the level surface f(x, y, z) = c of a differentiable function f. Then
f(x(t), y(t), z(t)) = C
Differentiating both sides of w.r.t x,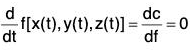
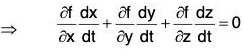
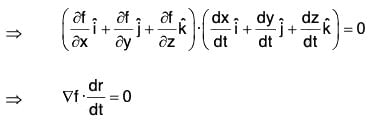
Hence ∇f is orthogonal to all vectors dr/dt = r in the tangent plane, i.e. ∇f is normal to the surface at every point along the curve.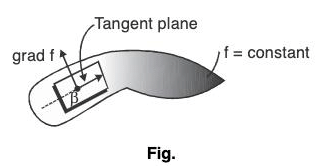
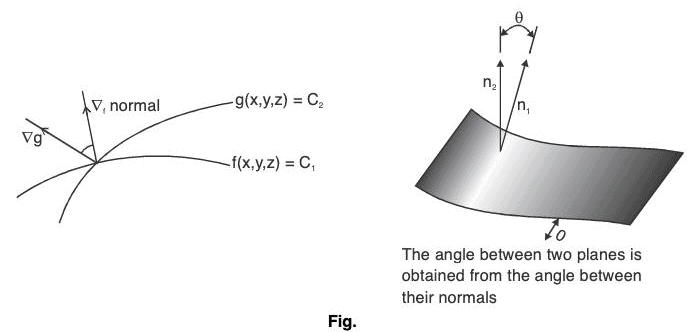
The angle between any two surfaces of f(x, y, z) = c1 and g(x, y, z) = c2 is the angle between their corresponding normal given by ∇f and ∇g respectively.
Let θ be the angle between the two surfaces. Then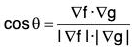
 Theorem : A scalar point function f is constant iff grad f = 0
Theorem : A scalar point function f is constant iff grad f = 0
Proof. Let f be a constant scalar point function, then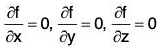
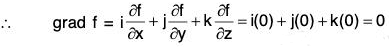
Conversely : Let grad f = 0, then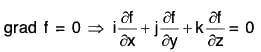
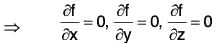
⇒ f is independent of x, y and z.
⇒ f is constant scalar point function.
Hence f is a constant scalar point function ⇔ ∇f = 0.
Operator a-∇
If a = a1i + a2j + a3k, then the operator a·∇ is defined as :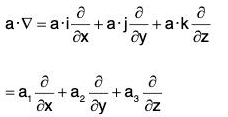
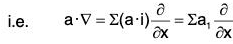
Therefore if f is any scalar point function, then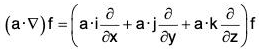
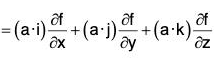
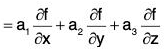 .....(1)
.....(1)
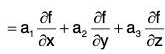 ....(2)
....(2)
Thus from (1) and (2), we have (a·∇)f = a·∇f
Example 1: If f(x, y, z) = 3x2y - y3z2 ; find the value of grad f at the point (1, -2, -1).
= i(6xy) + j (3x2 - 3y2z2) + k (-2y3z)
= 6xyi + (3x2 - 3y2z2) j - 2y3z k
Substituting x = 1, y = -2, z = -1,
grad f = 6(1)(-2)i + (3 - 3.4.1)j - 2(-8)(-1)k
= -12i - 9j - 16k
Example 2: If r = Irl, where r = xi + yj + zk, prove that:
(a) 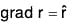
(b) 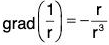
(c) ∇f(r) = f'(r)∇r
(d) ∇f(r) x r = 0
(e) grad rm = mrm-2 r
∵ r2 = x2 + y2 + z2
(d) Earlier it has been proved that
Sinceand the angle between same vector is zero so sin θ = sin (0) = 0
= mrm-2 (xi + yj + zk) = mrm-2 r
Example 3: If a, b be any constant vectors and r = x i + y j + z k; then prove that :
(a) ∇(a · r) = a
(b) V[r a b] = a x b
(a) Let a = a1i + a2j + a3k, where a1, a2, a3 are constants.
Then a·r = (a1i + a2j + a3k) · (xi + yj + zk)
= a1x + a2y + a3z
= i(a1) + j(a2) + k(a3) = a1i + a2j + a3k
= a.
(b) ∇[r a b] = ∇[r · (a x b)] [by notation]
= ∇[r · A], where A = a x b is a constant vector.
= ∇[A · r] = A [by (a)]
= a x b.
Example 4: lf u = x + y + z, v = x2 + y2 + z2 and w = yz + zx + xy prove that :
(grad u) · {grad v x grad w} = 0
= i(1) + j(1) + k(1) = i + j + k ....(1)= i(2x) + j(2y) + k(2z) = 2(xi + yj + zk) .....(2)
and from w = yz + zx + xy,
= i(y + z) + j(z + x) + k(x + y)
= (y + z)i + (z + x)j + (x + y)k .....(3)
Now from (1), (2) and (3),
= 2 [y(x + y) - z(z + x)] i - 2 [x(x + y) + z(y + z)] j + 2 [x(x + z) - y(y + z)]k
Simplify the above equation, we will get
= 0
Directional Derivative:
Definition: Let f(x, y, z) be a scalar point function in any region R and at any pint P(x, y, z) of this region 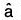 be a unit vector in any direction. If as is a small distance from P in the direction
be a unit vector in any direction. If as is a small distance from P in the direction 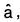 then
then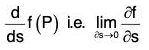
is called the directional derivative at the point P on the function f in the direction of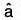 . If ∂s is taken in the direction of x-axis, then this will be ∂x.
. If ∂s is taken in the direction of x-axis, then this will be ∂x.
Hence ∂f/∂x is the directional derivative of f(x, y, z) is the direction of x-axis.
Similarly ∂f/∂y and ∂f/∂z are the directional derivatives of f(x, y, z) in the directions of y-axis and z-axis respectively.
Some theorem related to Directional Derivatives:
Theorem: The directional derivative of a scalar field f at a given point P(x, y, z) in the direction of a unit vector â is given by: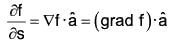
Proof. Let f(x, y, z) be a scalar point function in any region R and position vector of any point P(x, y, z) in this region is r = xi + yj + zk. If the distance of the point P from a fixed point A in the direction of â be s, then δs will represent a small distance at P in the direction â.
Hence dr/ds will be a unit vector at point P in the direction of â. Therefore 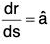
But r = xi + yj + zk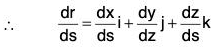
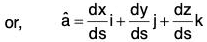 ...(1)
...(1)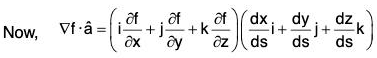 [by (1)]
[by (1)]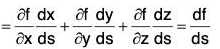
= the directional derivative of f at point P in the direction of â.
Theorem: ∇f (= grad f) is a vector normal to the surface f(x, y, z) = c where c is a constant.
Proof. Let P(x, y, z) be a point on the surface f(x, y, z) = c and Q(x + δx, y + δy, z + δz) be its neighbouring point on this surface.
Let r = xi + yj + zk and r + δr = (x + δx)i + (y + δy)j + (z + δz)k which are the position vectors of P and Q respectively.
Therefore 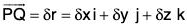 ...(1)
...(1)
When Q → P, then the line PQ tend to the tangent at the point P on the given surface.
Hence in the limiting position, (1) becomes
dr = dx i + dy j + dz k ......(2)
which lies in the tangent plane at the point P on the surface.
Again by Differential Calculus,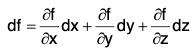
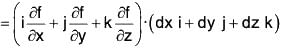
= ∇f · dr [by (2)]
But f(x, y, z) = constant ⇒ df = 0
Hence ∇f.dr = 0 ⇒ ∇f perpendicular to the vector dr.
⇒ ∇f is perpendicular to the tangent plane at P on the surface.
[∵ dr lies in the tangent plane at P on the surface.]
⇒ ∇ f i.e., grad f is normal to the surface f(x, y, z) = c.
Theorem: If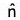 be a unit vector normal to the level surface f(x, y, z) = c at a point P in the direction of f increasing and n be the distance of P from a fixed point A in the direction of
be a unit vector normal to the level surface f(x, y, z) = c at a point P in the direction of f increasing and n be the distance of P from a fixed point A in the direction of 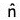 , then.
, then.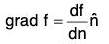
Proof. By theorem grad f is normal to the plane f(x, y, z) = c, therefore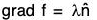 ....(1)
....(1)
where λ is any constant.
Again by theorem
(grad f) · n = ∂f/∂n ....(2)
From (1) and (2),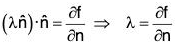
Substituting the value of λ in (1),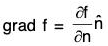
Remark : Igrad fl = I∇fl = ∂f/∂n
Theorem: grad f is a vector in the direction in which the maximum value of df/ds (directional derivative) occurs.
Proof. We know that the directional derivative of f in the direction of â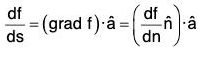 [by theorem]
[by theorem]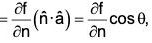
where θ is the angle between the vectors 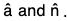
Now since ∂f/∂n is given, therefore the value of df/ds depend on cos θ.
Hence the value of df/ds will be maximum when θ = 0 i.e. when â is in the direction of 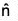 i.e., when â is in the direction of the normal to f.
i.e., when â is in the direction of the normal to f.
i.e. maximum directional derivative of f is in the direction of the normal to the plane and the value of the maximum directional derivative.
df/dn = |grad f|.
Vector equation of the Tangent plane:
The vector equation of the tangent plane to the surface f(x, y, z) = c.
Let P(a, b, c) be a point in the given plane whose position vector is
Therefore r0 = ai + bj + ck
Let Q(x, y, z) be a point on the tangent plane at P whose position vector is r, therefore r = xi + yj + zk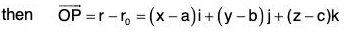
Now since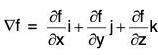
is the direction of the normal to the plane and 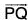 is perpendicular to ∇f being in the tangent plane.
is perpendicular to ∇f being in the tangent plane.
(r - r0) · ∇f = 0
which is the vector equation of the tangent plane to the surface at the point P.
Vector Equation of the Normal
The vector equation of the normal to the surface f(x, y, z) = c.
Take Q(x, y, z) any point on the normal at the point P whose position vector is r, then 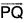 and ∇f will be parallel, PQ being normal to the surface
and ∇f will be parallel, PQ being normal to the surface
∴ (r - r0) x ∇f = 0
which is the vector equation of the normal to the surface at P.
Example 1: Find the directional derivative of f = xy + yz + zx in the direction of the vector i + 2j + 2k at the point (1, 2, 0)
Here ϕ = xy + yz + zx
= i(y + z) + j(z + x) + k(x + y) = (y + z)i + (z + x)j + (x + y)k
∴ At the point (1, 2, 0).
∇ϕ = (2 + 0)i + (0 + 1)j + (1 + 2)k = 2i + j + 3k .....(1)
Again if â is the unit vector in the direction of the vector i + 2j + 2k....(2)
Therefore the required directional derivative = (∇ϕ)·â[(by (1) and (2)]
= 10/3
Example 2: For the function 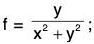 find the magnitude of the directional derivative making an angle 30° with the positive x-axis at the point (0, 1).
find the magnitude of the directional derivative making an angle 30° with the positive x-axis at the point (0, 1).
f = y/(x2 + y2)
Therefore at the point (0, 1), ∇f = i(0) + j(-1) = - j ....(i)
Again if â is the unit vector which makes an angle 30° with the positive direction to x-axis at the point (0, 1), then
∴ Required directional derivative = (∇f)·â[by (1) and (2)]
Example 3: Find the angle between the surface x2 + y2 + z2 = 9 and z = x2 + y2 - 3 at the point (2, - 1, 2).
Let f(x, y, z) ≡ x2 + y2 + z2 - 9 = 0
ϕ(x, y, z) ≡ x2 + y2 - z - 3 = 0
= 2xi + 2yj + 2zk
Therefore at the point (2, -1, 2), grad f = 4i - 2j + 4k .....(1)
= 2xi + 2yj - k
∴ At the (2, - 1 , 2), grad f = 4i - 2j - k ......(2)
Now since grad f is in the direction of the normal tot he surface f(x, y, z), therefore at the point (2, -1, 2), the angle between the surfaces f(x, y, z) and ϕ(x, y, z) is the angle between grad f and grad ϕ. If this angle is θ, then
Therefore the required angle
Example 4: Find the direction and magnitude of maximum directional derivative of f = x2 y z3 at the point (2, 1, -1).
The directional derivative of any scalar point function at any point is maximum in the direction of the gradient.
= (2xyz3)i + (x2z3)j + (3x2y z2)k
∴ At the point (2, 1, - 1), grad f = - 4i - 4j + 12 k
Therefore the direction of the maximum directional derivative at the point (2, 1, -1)
= -4i - 4j + 12k
Again the magnitude of the directional derivative at the point (2, 1 , - 1)
= Igrad fl
Example 5: Find a unit vector normal to the surface x2 y + 2xz = 4 at the point (2, -2, 3).
Let f(x, y, z) ≡ x2 y + 2xz - 4
We know that grad f is a vector in the direction of normal at the point (x, y, z) to the surface f(x, y, z) = c.
= (2xy + 2z)i + x2j + 2xk
∴At point (2, - 2 , 3), grad f = - 2 i + 4j + 4k
Therefore -2i + 4j + 4k is a vector in the direction of normal at the point (2, -2, 3) on the given surface. Therefore unit vector at the point (2, -2, 3) normal to the surface.
Example 6: Find the equations of the tangent plane and the normal to the surface xyz = 4 at the point (1, 2, 2).
The given surface f(x, y, z) = xyz - 4
Let co-ordinates of any point on the surface f be (x, y, z) and position vector be r. If r0 be the position vector of the point (1, 2, 2), then
r - r0 = (xi + yj + zk) - (i + 2j + 2k)
= (x - 1)i + (y - 2)j + (z - 2)k
At the point (1, 2, 2), grad f = 4i + 2j + 2k
The equation of the tangent plane at (1, 2, 2) (r - r0)·grad f = 0
⇒ {(x - 1)i + (y - 2)j + (z - 2)k} · (4i + 2j + 2k) = 0
⇒ 4(x - 1) + 2(y - 2) + 2(z - 2) = 0
⇒ 2x + y + z = 6
Again equation of the normal at the point (1, 2, 2) (r - r0) x grad f = 0
⇒ {(x - 1)i + (y - 2)j + (z - 2)k} x (4i + 2j + 2k) = 0
⇒ (y - z)i + (2z - x - 3)j + (x - 2y + 3)k = 0
⇒ y - z = 0 = 2z - x - 3 = x - 2y + 3
⇒ (x+3)/2 = y = z
Divergence of A Vector Point Function
Definition: If f(x, y, z) is a continuous and differentiable vector point function, then the divergence of f is expressed as div f or ∇·f and defined as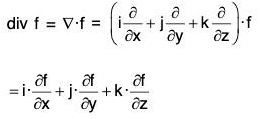
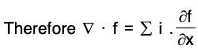
From the definition it is clear that the divergence of the vector point function is a scalar point function.
If the divergence of any vector f is zero i.e., if
div f = ∇·f = 0
then this is called solenoidal vector.
Remark: ∇·f ≠ f·∇, because f · ∇ is an operator and not a vector.
Theorems on Divergence
Theorem: If f(x, y, z) be a continuous differentiable vector point function and f = fxi + fyj + fzk, then div 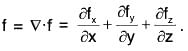
Proof. ∵ f = fxi + fyj + fzk, Therefore by definition,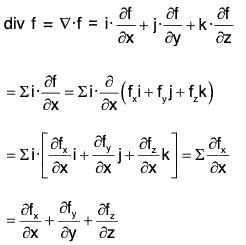
Theorem: If f and g be two differentiable vector point functions;
then div(f + g) = div f + div g
i.e., ∇·(f + g) = ∇·f + ∇·g
Proof. div(f + g) = ∇·(f + g)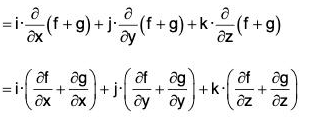
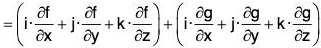
= ∇·f + ∇·g
= div f + div g
Theorem: If a is constant vector, then div a = 0.
Proof. ∵ a is a constant vector,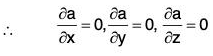
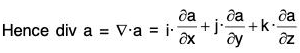
= 0 + 0 + 0 = 0
Example 1: If f = xy2i + 2x2 yz j - 3yz2k ; find div f at the point (1, - 1, 1).
div f = ∇·f
= y2 + 2x2z - 6yz
∴ At the point (1, -1, 1), div f = 1 + 2 + 6 = 9.
Example 2: If f = xy sin zi + y2 sin x j + z2 sin xy k, then find ∇·f at
= y sin z + 2 y sin x + 2z sin xy
Example 3: If f = (ax + 3y + 4z)i + (x - 2y + 3z)i + (3x + 2y - z)k is a solenoidal vector, find a.
Since f is a solenoidal vector, therefore ∇·f = 0
⇒ a - 2 - 1 = 0 ⇒ a = 3
Example 4: If r = xi + yj + zk, prove that:
(a) div r = 3
(b) 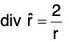
(c) 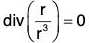
Example 5: If r = xi + yj + zk and r = Irl; prove that:
div rnr = (n + 3)rn
Hence show that rn r will be solenoidal, if n = -3
div rn r = ∇·rn r
= 3rn + nrn-2 (x2 + y2 + z2)
= 3rn + nrn-2 (r2) = (n + 3)rn
Again rn r will be solenoidal, if div rn r = 0
⇒ (n + 3)rn = 0
⇒ n + 3 = 0 [∵ r ≠ 0]
⇒ n = -3
Example 6: If a is a constant vector and r = xi + yj + zk;
prove that: ∇·(r x a) = 0
Let a = a1i + a2j + a3k, then
= i(a3y - a2z) + j(a1z - a3x) + k(a2x - a1y)= 0 + 0 + 0 = 0
Aliter:
= ∑i·[i x a + r x 0]
= ∑i·(i x a) = ∑[iia]
= ∑ 0 = 0
Example 7: If r = xi + yj + zk and r = Irl; prove that: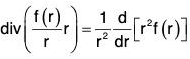
Curl of a Vector Point Function
Definition: If f(x, y, z) is a continuous and differentiable vector point function, then the curl of f is expressed as curl f or ∇×f and defined as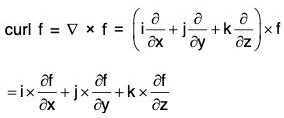
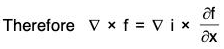
From the definition it is clear that the curl a vector point function is vector.
Irrotational Vector: If the curl of any vector f is zero vector, i.e. if
curl f = ∇ × f = 0
Then this is called an irrotational vector.
Theorems on Curl
Theorem: If f = f1i + f2j + f3k is a differential vector point function, then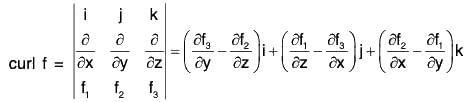
Proof. By definition,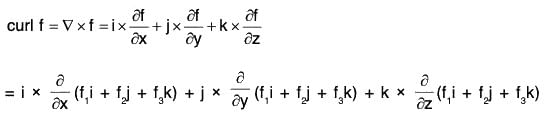
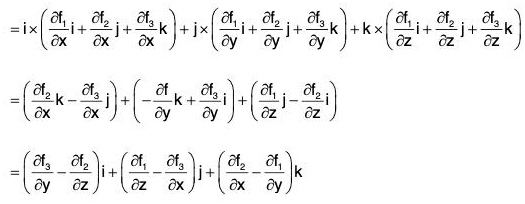
Remark: The above relation can be written in the determinant form as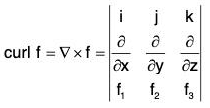
It should be kept in mind that the operators ∂/∂x , ∂/∂y , ∂/∂z , be written before the functions f1, f2, f3.
Theorem: If f and g be two differentiable vector point functions, then:
curl(f + g) = curl f + curl g
i e., ∇ × (f + g) = (∇ × f) + (∇ + g)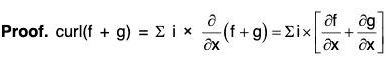
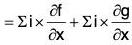
= curl f + curl g
∴ ∇(f + g) = (∇ × f) + (∇ × g)
Theorem: If a is a constant vector, then:
curl a = ∇ × a = 0
Proof. v a is a constant vector,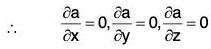
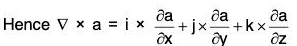
= 0 + 0 + 0 = 0
Example 1: If f = xy2i + 2x2yz j - 3 yz2k; find the value of curl at the point (1 , - 1 , 1)
= (-3z2 - 2x2y)i + (4xyz - 2xy)k
∴ At the point (1 , - 1 , 1)
curl f = (- 3 + 2)i + (- 4 + 2)k = -i - 2k.
Example 2: If f = (x + y + 1)i + j + (- x - y)k;
Prove that : f · curl f = 0
= (-1)i + (1)j + (-1) k = -i + j - k
∴ f · curl f = [(x + y + 1)i + j + (- x - y)k] · (-i + j - k)
= (x + y + 1)(-1) + (1)(1) + (- x - y)(-1)
= -x - y - 1 + 1 + x + y = 0.
Example 3: If V = ∇(x3 + y3 + z3 - 3xyz); find the following:
(a) div V
(b) curl V
V = ∇(x3 + y3 + z3 - 3xyz)
= 3(x2 - yz)i + 3(y2 - zx)j + 3(z2 - xy)k
(a) div V = ∇·V
= 6x + 6y + 6z = 6(x + y + z)
= 3∑(-x + x)i = 3∑0 = 0
Example 4: If f = exyz (i + j + k); find curl f.
= exyz [x(z - y)i + y(x - z)j + z(y - x)k]
Example 5: Prove that the following vector is irrational :
f = (sin y + z)i + (x cos y - z)j + (x - y)k
= (-1 + 1)i + (1 - 1)i + (cos y - cos y)k
= 0
Therefore f is an irrotational vector.
Example 6: If (xyz)b (xai + yaj + zak) is a irrotational vector, then prove that either b = 0 or a = -1.
Let f be the given vector, then
Now f is irrotational vector ⇒ curl f = 0 which is possible, when b(xyz)b = 0 or, za+1 - ya+1 = 0 = xa+1 - za+1 = ya+1 - xa+1
i.e. when b = 0 or, a + 1 = 0 ⇒ a = -1
Example 7: If r = xi = yj + zk and a is any constant vector ; then prove that: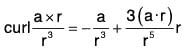
Let a = a1i + a2j + a3k, then
Some Important Vector identities
Identity I : div(u a) = u · div a + a · grad u
or, ∇·(u a) = u(∇·a) + a·(∇ u)
= u(∇·a) + (a·∇)u
Proof. By definition of divergence,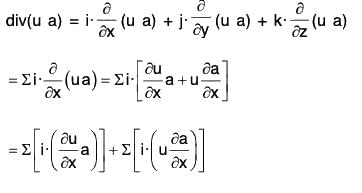
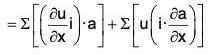 [∵ a · (nb) = (na) · b = n(a · b)
[∵ a · (nb) = (na) · b = n(a · b)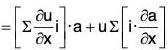
= (∇u)·a + u(∇·a) = u(∇·a) + a·(∇u)
Identity II: curl(u a) = (grad u) × a u curl a
or ∇ × (u a) = (∇ u) × a + u(∇ × a)
Proof. curl(u a) = ∇ × (u a)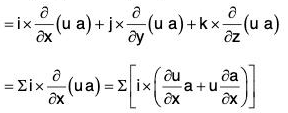
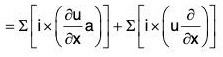
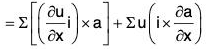 [∵ a × (nb) = (na) × b = n(a × b)]
[∵ a × (nb) = (na) × b = n(a × b)]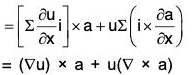
Identity III: div (a × b) = b curl a - a curl b
or, ∇·(a × b) = b·(∇ × a) - a·(∇ × b)
Proof. div (a × b) = ∇·(a × b)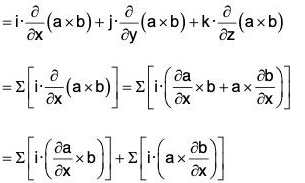
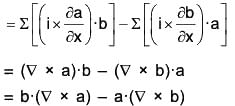
Identity IV: curl (a × b) = (b·∇)a - b div a - (a·∇)b + a div b
or, ∇ × (a × b) = (b·∇)a - b(∇·a) - (a·∇)b + a(∇·b)
Proof. curl(a × b) = ∇ x (a × b)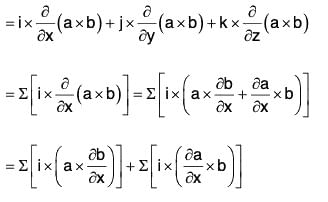
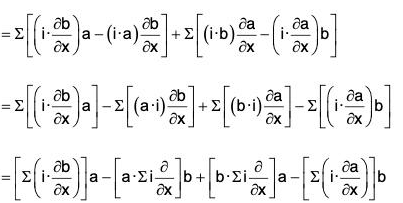
= (∇·b)a - (a·∇)b + (b·∇)a - (∇·a)b
= (b·∇)a - b(∇·a) - (a·∇)b + a(∇·a)
Particularly, when a is a constant vector, then
∇ × (a × b) = a(∇·b) - (a·∇)b
Identity V: grad(a·b) = (b·∇)a + (a·∇)b + b x curl a + a × curl b
or, ∇ (a·b) = (b·∇)a + (a·∇)b + b × (∇ × a) + a × (∇ × b)
Proof. grad(a·b) = ∇(a·b)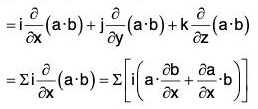
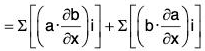 ....(1)
....(1)
∴ By vector triple product, a × (b × c) = (a·c) b - (a·b) c
⇒ (a·b)c = (a · c) b - a × (b × c)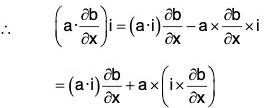
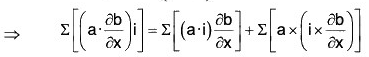
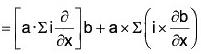
= (a·∇)b + a × (v × b) ...(2)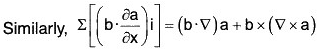
Substituting the values from (2) and (3) in (1),
grad (a·b) = (a·∇)b + a × (∇ × b) × (b·∇)a + b × (∇ × a)
= (b·∇)a + (a·∇)b + b × (∇ × a) + a × (∇ × b)
Second order differential function
We know that for any scalar point function ϕ, grad ϕ is a vector point function and for any vector point function f, div f is a scalar point function and curl f is a vector point function. Now since grad ϕ and curl f are vector functions, therefore their divergence and curl may exist.
Similarly, div f is a scalar function therefore gradient can be determined. Thus we can find (div(grad ϕ), curl(grad ϕ), div(curl f), curl(curl f) and grad(div f) which are called double order differentiable functions.
Property 1: div grad ϕ = ∇2ϕ
Proof. div grad ϕ = ∇·(∇ϕ)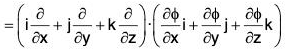
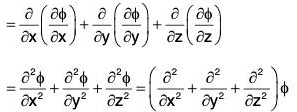
= ∇2ϕ
Remark : Laplacian operator ∇2: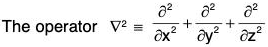
is called Laplacian operator and is equal to equal to ∇·∇ by property 1.
∇2ϕ = (∇·∇)ϕ = ∇·(∇ϕ)
This can be easily seen that
∇2ϕ = 0 ⇒ ∇2ϕx = 0,∇2ϕy = 0, ∇2ϕz = 0
Property 2: curl grad u = 0 = ∇ × (∇ u)
i.e. the curl of the gradient of a scalar function u is zero.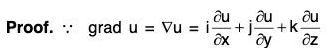
∴ curl grad u = ∇ × (∇u)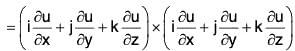

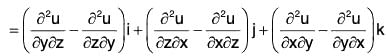
= 0i + 0j + 0k = 0
Property 3: div curl a = 0 = ∇·(∇ × a)
i.e. the divergence of curl of any vector a is zero.
Proof. Let a = a1i + a2j + a3k, then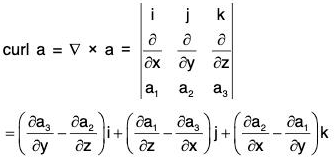
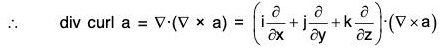
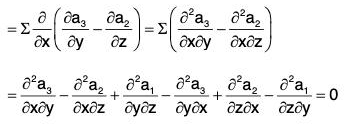
Property 4: curl curl a = grad div 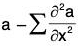
i.e., ∇ × (∇ × a) = ∇(∇·a) - ∇2a
Proof. Let a = a1i + a2j + a3k, then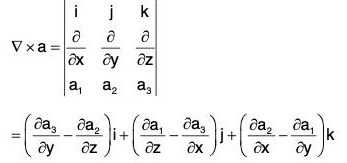
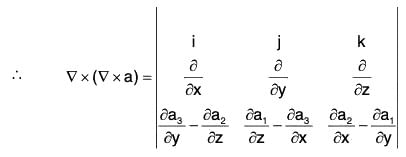
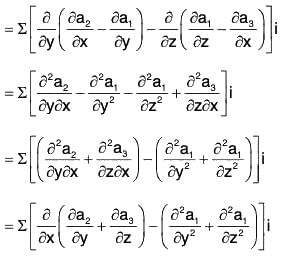
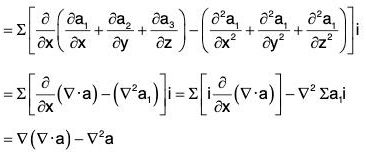
Example : Prove that: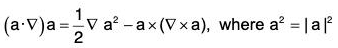
Integration of Vectors
Let f(t) be a finite, single valued and continuous vector function of the single scalar variable t, then the vector function of t, which when differentiated wrt t gives f(t) i.e. a vector function F(t) exist such that its differentiation wrt t.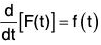
then F(t) is called the integral of vector function f(t) wrt t. In the symbolic form,
if dF(t)/dt = f(t)
then ∫t(t)dt = F(t), ...(1)
Here the vector function f(t) is called the integrand.
Vector constant of integration:
where the constant vector c is called the arbitrary constant vector of integration.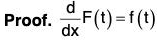 ....(1)
....(1)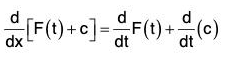
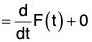 [∵ c is a constant vector]
[∵ c is a constant vector]
= f(t) [by (1)]
Therefore by definition,
∫f(t)dt = F(t) + c,
where the constant vector c is called the arbitrary constant vector of integration.
This constant vector of integration is determined by the initial conditions or geometrical conditions.
Indefinite Integral: Since in F(t) + c, c is an indefinite constant vector, therefore this is called an indefinite integral of f(t) wrt t.
Theorem: If f(t) = f1(t)i + f2(t)j + f3(t)k is a vector function of single function t, where f1(t), f2(t) and f3(t) are continuous in a particular region,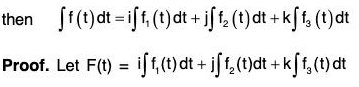
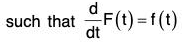 ...(1)
...(1)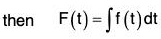 ...(2)
...(2)
Now by (1),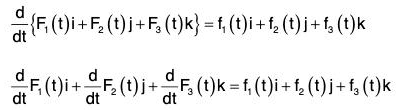
Comparing the coefficients of i, j and k,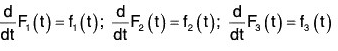
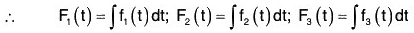
Therefore by (2),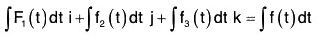
Hence to integrate a vector function, its components are integrated.
Some important results on integration
If f(t) and ϕ(t) are two continuous differential vector functions of scalar variable t expressed by f and ϕ, then with the help of Differential Calculus, their corresponding integrals can also be easily derived :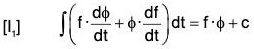
By differentiation, we have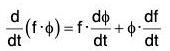
Now by definition, the required result is obtained.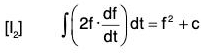
Taking f = ϕ in I1 ;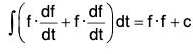
which gives the required result.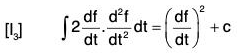
Replacing f by df/dt in I2,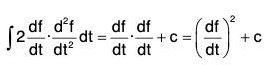
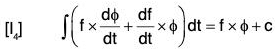
By differentiation, we have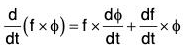
Therefore by definition,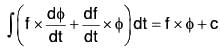
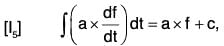 where a is a constant vector.
where a is a constant vector.
If a is a constant vector, then by differentiation,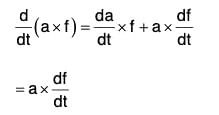
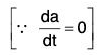
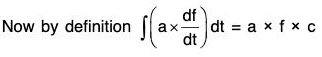
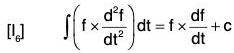
By differentiation, we have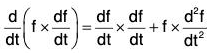
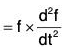
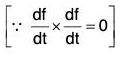
Now by differentiation, 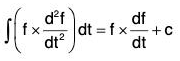
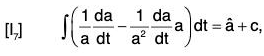
where â is a unit vector in the direction of a and lal = a.
We know that â = a/a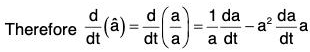
Now by definition,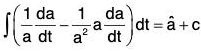
Remark: If the integrand is scalar (dot product) then the constant of integration is a scalar and if the integrand is vector (cross product) then the constant of integration is a vector.
Definite Integral: Definition:
If ∫f(t)dt = F(t), then F(b) - F(a)
is called definite integral of f(t) between the limits t = a and t = b.
and is written as 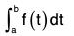
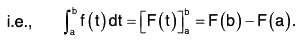
Example 1: Find : ∫f(t) dt, where f(t) = (t - t2)i + 2t3 j - 3k
Here the integral ∫{(t - t2)i + 2t3j - 3k}dt
= i∫(t - t2)dt + j∫2t3 dt - k∫3dt
where 0 = 0,1 + 02) + c3k.
Example 2: If r(t) = t i - t2 j + (t - 1)k and s(t) = 2t2 i + 6t k, then find the value of :
(a)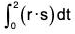
(b)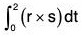
(a) r · s = {t i - t2 j + (t - 1)k} · {2t2 i + 6t k} = 2t - 2t2 - 21 + 2t2 + 12t
= 2t3 + 6t2 - 6t
= {- 6t3 i + 2t2(t - 4)j + 2t4 k}
Example 3: If r(t) = t i - 3j + 2t k; s(t) = i - 2j + 2k and v(t) = 3i + t j - k; then find the value of 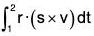
s × v = (i - 2j + 2k) × (3j + t j - k)
= (2 - 2t)i + 7j + (t + 6)k
and r · (s × v) = (t i - 3 j + 2t k) · {(2 - 2t)i + 7j + (t + 6)k}
= 14t - 21
Example 4: If r(t) = 2i - j + 2k, when t = 2 = 4i - 2j + 3k when t = 3 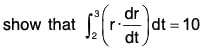
From the standard formulae of integrals, we have
....(1)
when t = 3 then r = 4i - 2j + 3k
and r2 = (4i - 2j + 3k)-(4i - 2j + 3k)
= 16 + 4 + 9 = 29 ....(2)
Again when t = 2 then r = 2i — j + 2k
and r2 = (2i - j + 2k) · (2i - j + 2k)
= 4 + 1 + 4 = 9 ....(3)[by (2) and (3)]
Example 5: Integrate : d2r/dt2 = -n2r
Since r is not known in terms of t on RHS, therefore it can not be integrated.
Scalar multiplication on both sides by
Now integrating both sides wrt t,
Using the earlier results. We have
where c is a scalar constant.
Example 6: Find the value of r from the equation d2r/dt2 = a + tb
Working method :
1. Solve the given equation treating vector variable as scalar variable.
2. Replace arbitrary scalars constants by arbitrary vector constants.
The given equation is
d2r/dt2 = a + tb .......(1)
Integrating both sides wrt t,....(2)
Again integrating wrt t,.....(3)
Replacing scalar constants by vector constants in (2) and (3),......(4)
.....(5)
By the given condition, when t = 0 then r = 0 and dr/dt = 0
Therefore by (4), c = 0 and d = 0
Therefore the required solution is
Example 7: The acceleration of a particle at any time t ≥ 0 is given by:
a = dv/dt = 12 cos 2t i - 8 sin 2t j + 16t k
If the velocity v and displacement r are zero at t = 0; find v and r at any time.
Solution. By the given problem dv/dt = 12 cos 2t i - 8 sin 2t j + 16 k
Integrating, v = i∫12 cos 2t dt - j∫8 sin 2t dt + k∫16t dt
or v = 6 sin 2t i + 4 cos 2t j + 8t2 k + c .....(1)
Initial condition, when t = 0, then v = 0
Therefore 0 = 0i + 4j + 0k + c ⇒ = - 4 j
Hence from (1) the required velocity,
v = 6 sin 2t i + (4 cos 2t - 4)j + 8t2 k ......(2)
Again integration (1),
r = i∫6 sin 2t dt + 4 j∫ (cos 2t - 1)dt + 8k ∫t2 dt ......(3)
......(3)
Initial condition, when t = 0, then r = 0
Therefore 0 = - 3 i + Oj + Ok + d ⇒ d = 3i
Therefore replacing from (3), the required
Line Integral
Definition: The integral obtained along any curve is called the line integral.
Let position vector of any point P on the curve C be r whose equation is r = f(t), where f(t) is the continuous and differential function.
The unit vector function along the tangent at any point P on the curve is dr/ds.
Let F(r) be a continuous vector point function. Now if the component of the vector function F(r) along the tangent at the point P be F(r) · dr/ds and the integral of 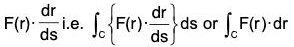 is called the line integral of the vector function F(r) on the curve C.
is called the line integral of the vector function F(r) on the curve C.
Cartesian form of Line Integral
Let F(r) = F1(t)i + F2(t)j + F3(t)k
and dr = dx·i + dy·j + dz·k, where r = xi + yj + zk
Therefore ∫cF(r)·dr = ∫c (F1i + F2j + F3k)·(idx + jdy + kdz)
or ∫c F·dr = ∫c(F1dx + F2dy + F3dz)
Circulation
Definition: The integral of the vector F along any closed curve i.e. c is called the circulation of F around the closed curve C.
If the circulation of a vector point function in any region is equal to zero around every closed curve in that region, then that vector is called the Irrotational vector.
Work done by a Force
Suppose a force F is a acting at a point and displaces it from a point A along the curve C. Let r be the position vector of the point A.
Since dr/ds is the unit vector along the tangent at the point A in the direction s increasing, therefore the component of F along the tangent at the point 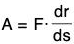
Therefore the work done by F at C on the curve during the small displacement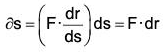
Therefore total work done by F = ∫c F·dr
Remark : If the path of integration is a closed curve, we write 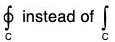
Example 1: Evaluate: ∫cF·dr, where F = (x2 + y2)i + xy j and C is the curve y = x2 is (0, 0) to (3, 9).
For the curve C, the values of x varies from 0 to 3 and the values of y varies from 0 to 9. Therefore
{∵ r = xi + yj}
{∵ y = x2}
Example 2: Evaluate ∫cF·dr, where F = xy i + yz j + zx k and C is the curve r = t i + t2 j + t3k, t varying form -1 to +1.
Around the curve C
r = xi + yj + zk .....(1)
Here r = ti + t2j + t3k .....(2)
From (1) and (2),
x = t, y = t2 and z = t3 ......(3)
From (2), dr/dt = i + 2t j + 3t2 k .....(4)
= ∫c {(xyi + yz j + zx k)·(i + 2t j + 3t2 k)} dt [by (4)]
= ∫c {(t3 i + t5 j + 14 k)·(i + 2t j + 3t2 k)} dt [by (3)]
Example 3: Evaluate : ∫cF·dr,
where F = zi + xj + yk, C is the arc of the curve r = cos t i + sin t j + t k from t = 0 to t = 2 π
From the equation of the curve,
dr = -sin t i + cos t j + k
The parametric equations of the curve
x = cos t, y = sin t, z = t .....(1)[by (1)]
= 2π + π - 1 + 1 = 3π
Example 4:
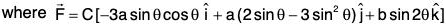 and the curve C,
and the curve C, 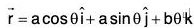 , where θ varies from π/4 to π/2.
, where θ varies from π/4 to π/2.
= C[3a2 sin2θ cosθ + a2(2 sinθ cosθ - 3 sin2θ cosθ) + b2 sin 2θ]
= C[3a2 sin2θ cosθ + a2 2sinθ cosθ - 3a2 sin2θ cosθ + b2 sin 2θ]
= C(a2 + b2) sin 2θ
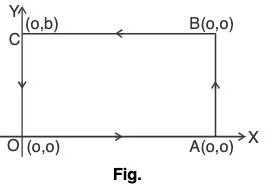
Example 5: Evaluate : ∫cF·dr, where F = (x2 + y2)i - 2xy j and curve C is the rectangle in the xy plane bounded by x = 0, x = a, y = 0, y = b.
In xy plane, z = 0, therefore r = xi + yj
∴ dr = dx i + dy j
Now ∫cF·dr = ∫c{(x2 + y2) i - 2 xy j}·(dx i + dy j)
= ∫c{(x2 + y2)dx - 2xy dy}
According to the question, the path of integration C is the rectangle OABC formed by the given straight lines.(a) On the side OA of the rectangle y = 0 ⇒ dy = 0 and the limit of x is 0 to a.
Therefore along the side OA of the rectangle,...(1)
(b) Similarly along the side AB of the rectangle
[x = a ⇒ dx = 0, y = 0, y = b]....(2)
(c) along the side BC of the rectangle by = b ⇒ dy = 0, x = a to x = 0.....(3)
(d) On the side CO of the rectangle [x = 0 ⇒ dx = 0, y = b, y = 0]
∫cF·dr = ∫c0dy = 0 ...(4)
Hence around the rectangle,
Example 6: Evaluate : ∫c(yz dx + (xz + 1)dy + xy dz), where C is any path from (1,0,0) to (2,1,4).
∫c{yz dx + (xz + 1)dy + xy dz}
= ∫c{yzi + (xz + 1)j + xy k}·(i dx + j d y + k dz)
= F·dr,
where F = yz i + (xz + 1)j + xy k and r = xi + yj + zk
Let the given path be a straight line from to point (1, 0, 0) to the point (2, 1, 4), therefore
then x = t + 1 , y = t , z = 4t
∴ F = 4t2 i + (4t2 + 4t)j + (t2 + t)k
and r = (t + 1)i + t j + 4t k
Therefore dr = (i + j + 4k)dt
∴ From the point (1, 0, 0), t = 0 and for the point (2, 1, 4), t = 1
Example 7: Find the total work done in moving a particle in a force field given by F = 3xy i - 5zj + 10k along the curve x = t2 + 1, y = 2t2, z = t3 from t = 1 to 2.
We know that r = x i + y j + z k
Therefore dr = dx i + dy j + dz k
Now F·dr = (3xy i - 5zj + 10k)-(dx i + dy j + dz k)
= 3x y dx - 5z dy + 10x dz
From the equation of the curve,
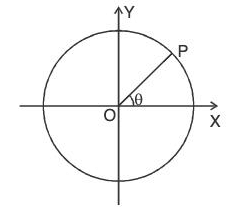
Example 8: 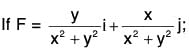 find the circulation of F in the anticlockwise direction round the circle x2 + y2 = 1 situated in the z-plane.
find the circulation of F in the anticlockwise direction round the circle x2 + y2 = 1 situated in the z-plane.
The parametric equations of the curve x = cos θ, y = sin 0, z = θ
∴ r = cos θ i + sin θ + 0k and dr/dθ = -sin θ i cos θ j
Now by definition, circulation around the circle
Properties of the integral
(1) 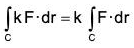 , where k is a constant
, where k is a constant
(2) 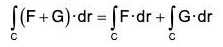
(3) 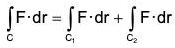
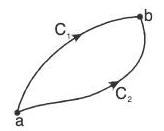
where C is the sum of two curves C1 and C2.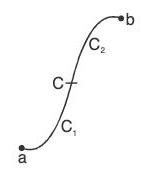 (4)
(4)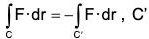 is the curve C taken in opposite sense.
is the curve C taken in opposite sense.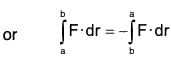
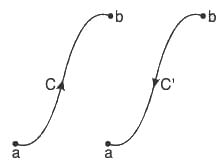 (5) The line integral is independent of the choice of representation but depends on the path of integration.
(5) The line integral is independent of the choice of representation but depends on the path of integration.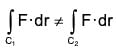
 (6) In case, the line integral depends only on the end points a and b, not on the path joining them, the vector field F is conservative vector field.
(6) In case, the line integral depends only on the end points a and b, not on the path joining them, the vector field F is conservative vector field.
Recall that if F = ∇ϕ, F is conservative field and ϕ is its scalar potential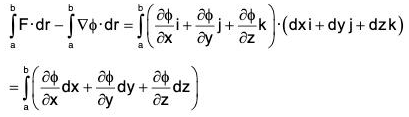
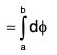
∴ 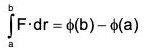
This formula should be applied whenever a line integral is independent of path.
Applications of Line Integral
(a) Work done by a force: The work done by a variable force F in the displacement along a curve C from point A to B is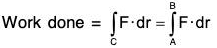 ....(1)
....(1)
Work done in conservative force field in moving a particle from A to B is independent of the path joining A and B and dependents only on the end points A and B.
In such case F = ∇ϕ, and hence
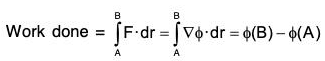
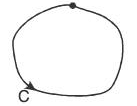
Also if A and B coincide, that is, C is any closed curve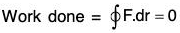 ....(2)
....(2)
(b) Circulation due to a velocity field: Let F denotes velocity of a fluid, then the circulation of F around a closed curve C is given by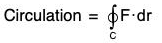
(c) Test for exact differential: For F = F1i + F2j + F3k the necessary and sufficient condition that F1dx + F2dx + F3dz be an exact differential is that F must be conservative, i.e. ∇ × F = 0.
⇒ These exist f such that F = ∇ϕ
Then F1dx + F2dy + F3dz = F·dr = ∇ϕ·dr = dϕ = Exact differential ...(3)
|
98 videos|27 docs|30 tests
|
FAQs on Vector Calculus - (Part - 1) - Mathematics for Competitive Exams
| 1. What is the difference between a scalar and a vector? |  |
| 2. What does the gradient of a scalar point function represent? |  |
| 3. What does the divergence of a vector point function indicate? |  |
| 4. How is the curl of a vector point function defined? |  |
| 5. What is the significance of line integrals in vector calculus? |  |

|
Explore Courses for Mathematics exam
|

|

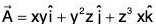 is a vector field.
is a vector field.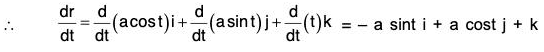
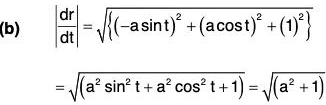
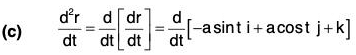
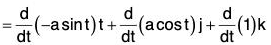
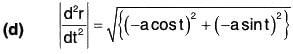
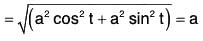
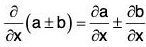
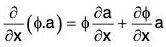
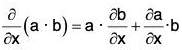
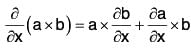
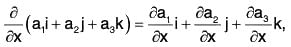
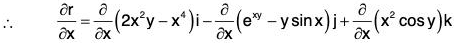
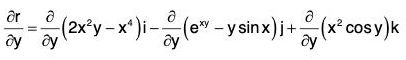
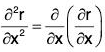
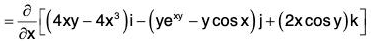 [by (1)]
[by (1)]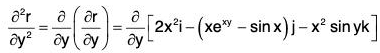 [by (2)]
[by (2)]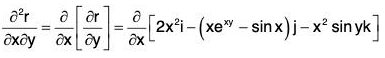 [by (2)]
[by (2)]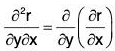
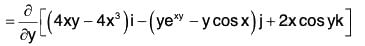 [by (1)]
[by (1)]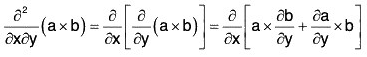
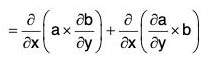
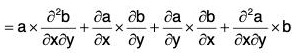 ....(1)
....(1)
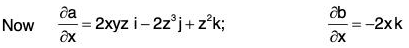

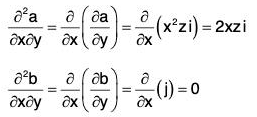
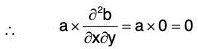 ....(2)
....(2)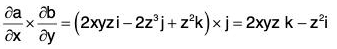 ....(3)
....(3)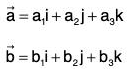
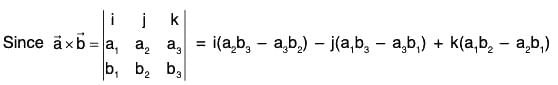
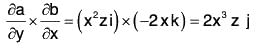 ....(4)
....(4)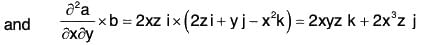
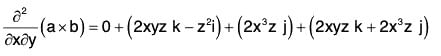
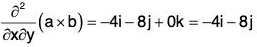
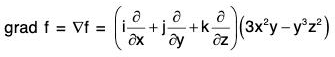
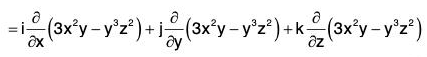
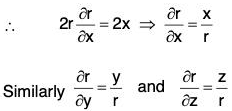
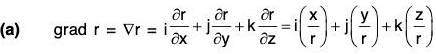
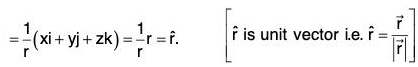
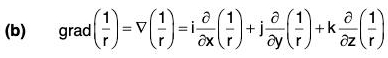
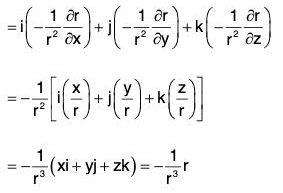
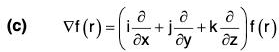
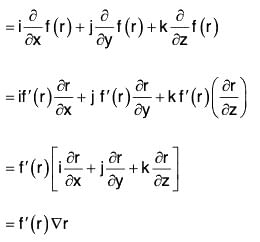
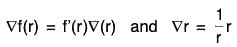
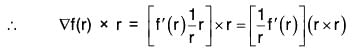
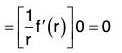
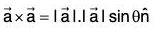 and the angle between same vector is zero so sin θ = sin (0) = 0
and the angle between same vector is zero so sin θ = sin (0) = 0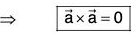
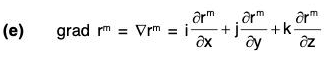
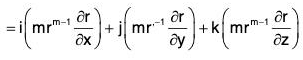
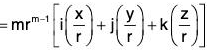
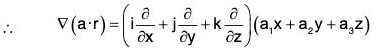
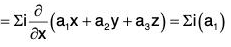
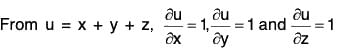
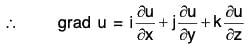
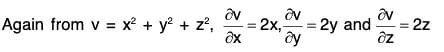
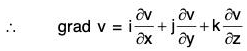
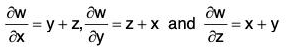
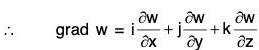
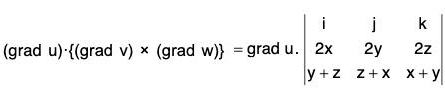
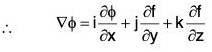
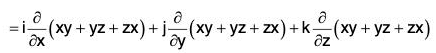
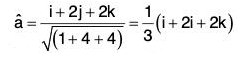 ....(2)
....(2)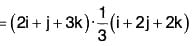
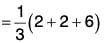 [(by (1) and (2)]
[(by (1) and (2)]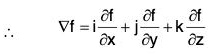
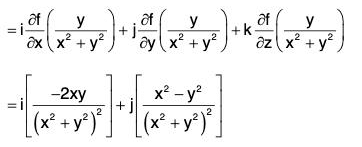
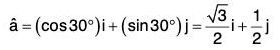
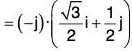 [by (1) and (2)]
[by (1) and (2)]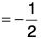
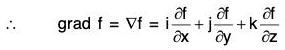
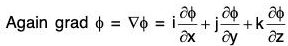
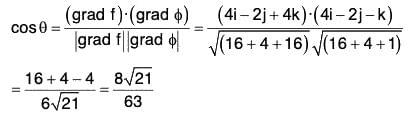
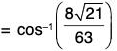
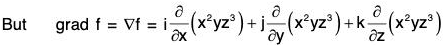
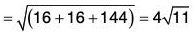
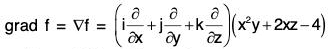
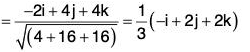
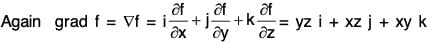
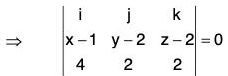
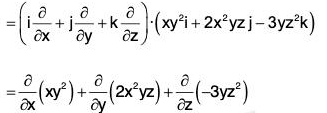
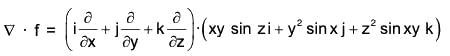
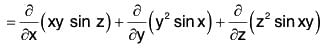
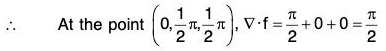
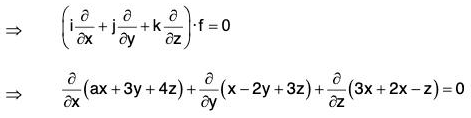
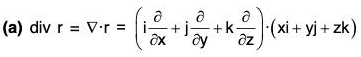
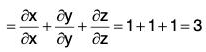
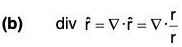
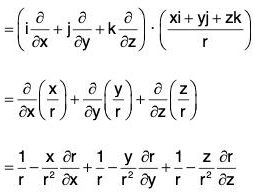
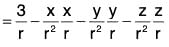
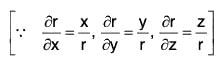
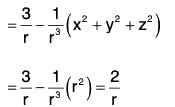
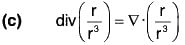
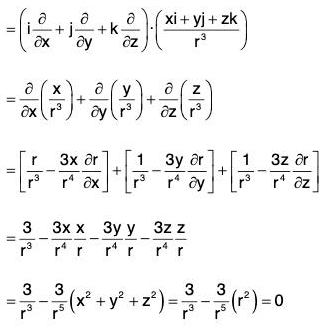
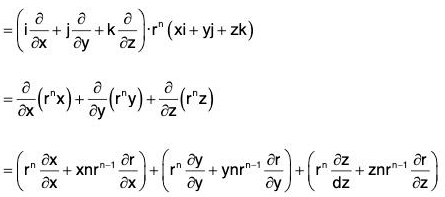
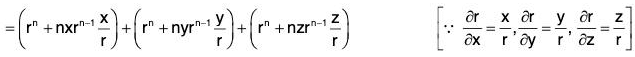
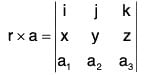
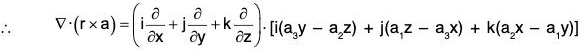
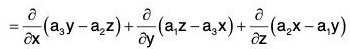
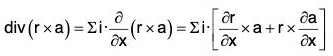
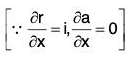
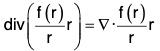
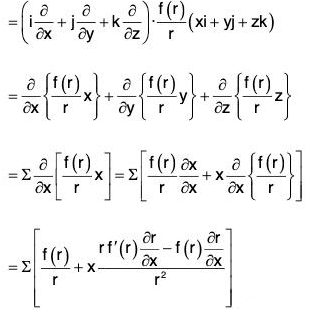
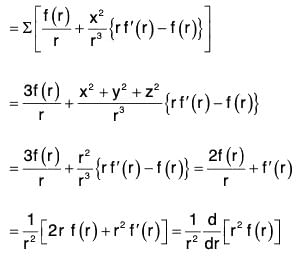
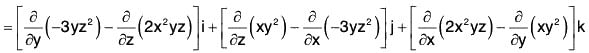
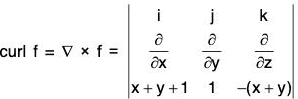
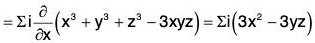
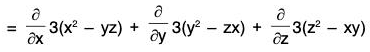
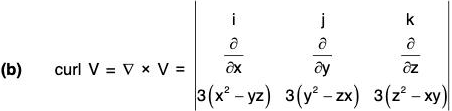
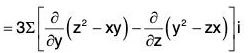
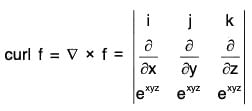
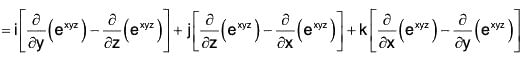
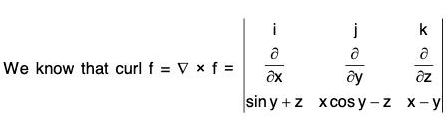
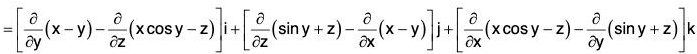
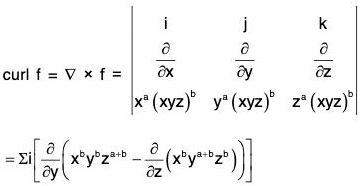
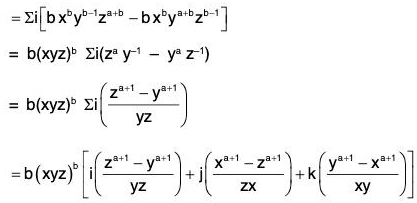
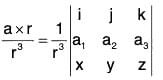
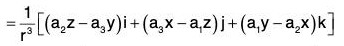
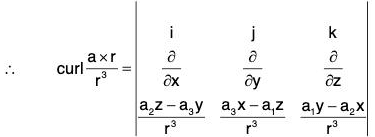
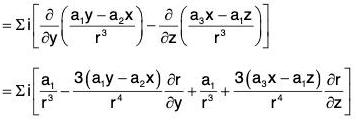
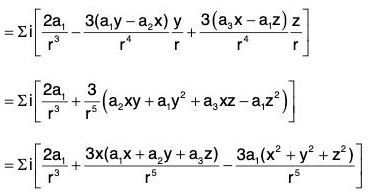
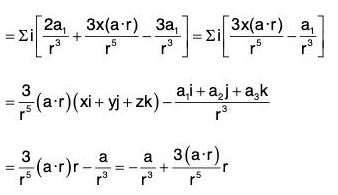
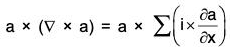
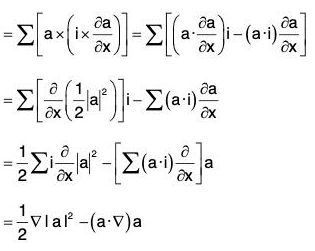
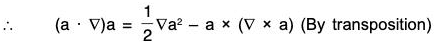
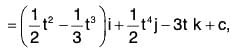
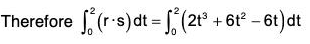
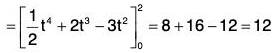
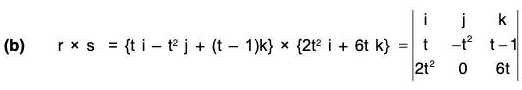
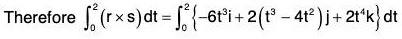
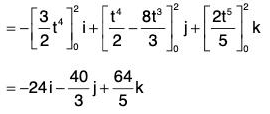
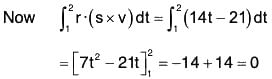
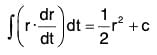
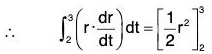
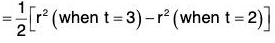 ....(1)
....(1)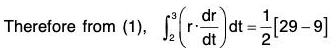 [by (2) and (3)]
[by (2) and (3)]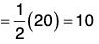
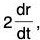
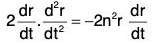
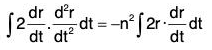
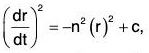
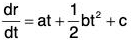 ....(2)
....(2)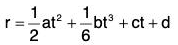 .....(3)
.....(3)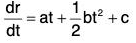 ......(4)
......(4)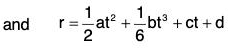 .....(5)
.....(5)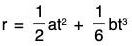
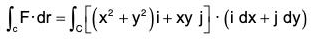 {∵ r = xi + yj}
{∵ r = xi + yj}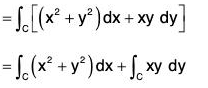
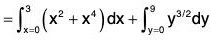 {∵ y = x2}
{∵ y = x2}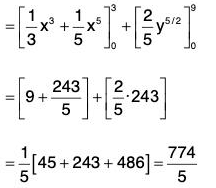
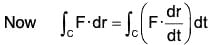
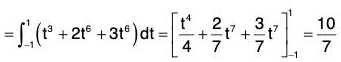
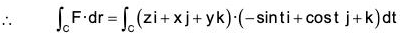
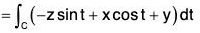
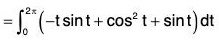 [by (1)]
[by (1)]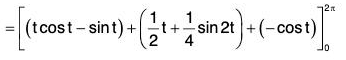
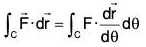
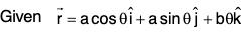
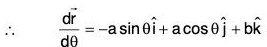
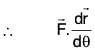 = C[3a2 sin2θ cosθ + a2(2 sinθ cosθ - 3 sin2θ cosθ) + b2 sin 2θ]
= C[3a2 sin2θ cosθ + a2(2 sinθ cosθ - 3 sin2θ cosθ) + b2 sin 2θ]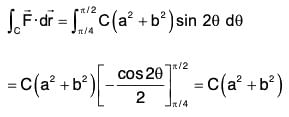
 (a) On the side OA of the rectangle y = 0 ⇒ dy = 0 and the limit of x is 0 to a.
(a) On the side OA of the rectangle y = 0 ⇒ dy = 0 and the limit of x is 0 to a. 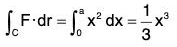 ...(1)
...(1)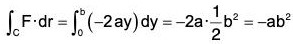 ....(2)
....(2)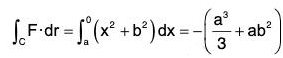 .....(3)
.....(3)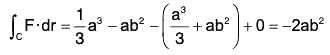
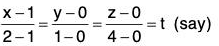
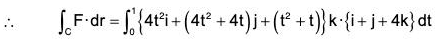
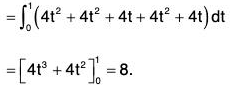
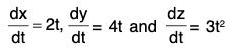
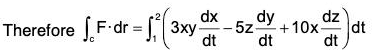
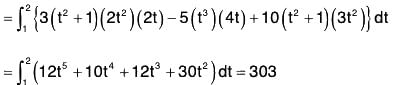
 ∴ r = cos θ i + sin θ + 0k and dr/dθ = -sin θ i cos θ j
∴ r = cos θ i + sin θ + 0k and dr/dθ = -sin θ i cos θ j