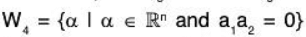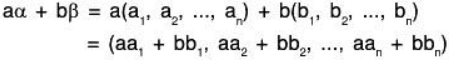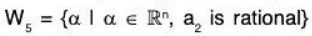Vector Space & Linear Transformation - 1 | Mathematics for Competitive Exams PDF Download
Vector Spaces
By now, you must have studied the algebraic structures consisting of one set and one or two binary compositions only.
For example
- one set and one binary composition in a Group and
- one set and two binary composition in a Group.
Ring, Integral Domain, Field etc.
Now here we shall study the structure consisting of two sets, (a field and an abelian group) and a composition combining an element of the field to an element of the abelian group. In fact, this is the most fundamental and basic structure in which the concept of distance and hence the concept of limits etc can be introduced, leading to the study of analysis in a much wider prospect. Thus this serves as a link between algebraic and topological structure.
Some Definitions
➤ Ring
Definition: A non-empty set R is called ring if
- R is abelian group under addition
- R is semi-group under multiplication
- Distribution law holds
a(b + c) = a • b + a • c
(a + b)c = a • c + b • c
Example
(i) (Z, +, •) is a ring where Z = {0, ±1, ±2, ...}
(ii) (Q, +, •), where Q is the set of rational numbers.
(iii) (R, +, •), where R is set of real numbers.
(iv) (Zn, +, •), Zn = residue classes of module n.
➤ Field
Definition: A non-empty set F is called a field if
- F is abelian group under addition
- F - {0} is abelian group under multiplication
- Right distribution law holds in F.
i.e. a, b, c, e F
(a + b)c = ac + be
Example
(i) (R, +, •) is a field
(ii) (C, +, •) is a field
(iii) (Q, +, •) is a field
(iv) (Z, +, •) is not field as (Z - {0}, •) is not group under multiplication.
- Vectors: Let V be a non-empty set whose element α,β, γ,.... or v1, v2, v3, ........ etc. will be called vectors.
- Scalars: Let (F, +, .) be a field whose element α,β, γ..... will be called Scalars.
- Internal Binary Composition (Vector addition): A map * : V * V →V is called an internal composition in V and denoted by '+’ . i.e., for every α ∈ V , β ∈ V , α * γ∈ V
Example: In the set Z of integers, the addition and multiplication are internal binary compositions. - External Binary Composition (Scalar Multiplication): A map o : F * V → V is called an external composition in V and denoted by 'o’ or '•'.
i.e., ∀ a ∈ F and ∀ a ∈ V, a o α ∈ V,
Example: In the set of matrices, scalar multiplication of matrices is an external binary operation on the R of real numbers.
The following defines the notion of a vector space V where K is the field of scalars.
Definition: Let V be a nonempty set with two operations:
(i) Vector Addition: This assigns to any u, v, ∈ V a sum u + v in V.
(ii) Scalar Multiplication: This assigns to any u ∈ V, k ∈ K a product ku ∈ V.
Then V is called a vector space (over the field K) if the following axioms hold for any vectors u, v, w ∈ V:
[A1] (u + v) + w = u + (v + w)
[A2] There is a vector in V, denoted by 0 and called the zero vector, such that, for any u ∈ V, u + 0 = 0 + u = u
[A3] For each u ∈ V, there is a vector in V, denoted by - u and called the negative of u, such that u + ( - u) = ( - u) + u = 0
[A4] u + v = v + u
[M1] k(u + v) = ku + kv, for any scalar k ∈ K.
[M2] (a + b)u = au + bu, for any scalar a, b ∈ K.
[M3] (ab)u = a(bu), for any scalar a, b ∈ K.
[M4] 1 u = u, for the unit scalar 1 ∈ K.
Notation: Generally, the vector space V over the field F is expressed by V(F). When the field F itself is clear, then it is expressed simply by V only.
Throughout in the text, V(F) will mean a vector space V of vectors over a field F of scalars If F = R (the field of real numbers), then V(R) is called a Real vectors over a field F of scalars.
Space
Similarly V(ℂ) is called the Complex Vector Space and V(ꙩ) is called the Rational Vector Space. The set of three dimensional vectors of geometry is called Three Dimensional Vector Space and is written as V3(F) or V3(F) or simply V3.
Important Remarks:
- Here by vector we do not mean the vector quantity which we have defined in Vector algebra as a directed line segment.
Here the word vectors and scalars will used in more general sense. - Four operations have been used in the vector space V(F), Two different internal operations (+), (•) in the field F,
Third internal operations (+) in the set V and the fourth external operations (•) in V over F.
Though in these four operations, two are expressed by the symbol (+) and remaining two by the symbol (•), but it should be clear that under the reference which symbol (+), or (•) is being used for which operation.
For Example, if a, b ∈ F , then a + b ∈ F express the addition in the field F which is often called the scalar addition in the field F and if α, β ∈ V then α + β ∈ V express the addition in the set V which is generally called the vector addition. Similarly a • b G f express the multiplication in the field F and a • b ∈ V express the external operation scalar multiplication of the vector space. - Two type of zero element have been used in every vector space. Zero element i.e. additive identity of V will be indicated by hold face type ‘0’ and is called zero vector and zero element of the field F is generally indicated by ‘0’ which is called zero scalar. In future text we shall indicated both of these by the same symbol ‘0’ and the context will make it clear, which zero we intend.
- The vector space which contains only zero element is called Null space or Trivial space and is written as {0}.
Examples of Vector space
Example 1: Every field is a vector space over its subfield.
Let F be a field and H be its subfield. Then F is an abelian group for the usual addition.
Also a ∈ H, x ∈ F ⇒ a ∈ F, x ∈ F ⇒ ax ∈ F
Hence usual multiplication in F can be taken as external composition.
Now we verify the various postulates of a vector space in F(H):
V1. (F, +) is an abelian group .V2. For every a ∈ Hand α,β ∈ F
a(α + p) = aα + ap [By distributivity in F]
V3. For every a, b ∈ Hand α,∈ F
(a + b) a = aα + bα [By distributivity in F]
V4. For every a, b∈ H and a, ∈ F
(ab)α = α(bα) [By multiplicative associativity]
V5. If 1 is the unity element of R then
1α = α,∀α∈ F [∵ 1 is multiplicative identity in F]
Therefore F(H) is a vector space.
Special Case: Since every field is also a subfield of itself, therefore F(F) is a vector space. Consequently, ℂ(ℂ), ℝ (ℝ ), ꙩ(ꙩ) are also vector space for the ordinary and multiplication.
Remark: C(R) and R(ꙩ) are vector space, but R(C) and ꙩ(R) are not vector spaces, because they are not closed for scalar multiplication.
Example 2: The set Fn of all ordered n-tuples of a field F is a vector space over the field F.
Let Fn = {(a1, a2,......,an) I a1, a2,.......,an ∈ F}
and α = (a1,a2,....., an), β = (b1, b2,.....,bn) and a∈F.
We define the addition of n-tuples asα + β = (a1 + b1, a2 + b2,....an + bn) ...(1)
and scalar multiplication of n-tuples as
aα = a(a1, a2,..., an) = (aa1, aa2,......,aan) ...(2)
Clearly, α, β ∈ F and a∈ Fn.
α + β ∈ Fn ∀ α, β ∈ Fn and a ∈ F, α ∈ Fn => aα ∈ FnTherefore Fn(F) is closed for the above defined addition and scalar multiplication operations.
Verification of Space axioms:
V1. It can also be easily verified that Fn is an abelian group for the addition defined above and 0 = (0, 0 .....0) ∈ Fn being the additive identity and -- α = ( -a1, -a2,. . . , - an) ∈ Fn being the additive identity in verse of α = (a1, a2,...., an) ∈ Fn.
V2. Scalar Multiplication is distributive over vector addition:
Let a ∈ F and α.β ∈ Fn; thena = (α + β) = a {(a1, a2,...., an) + (b1, b2,...., bn)}
= a (a1 + b1, a2 + b2,...an + bn) [by (1) ]
= {a(a1 + b1), a(a2 + b2),..... a(an + bn)} [by (2) ]
= (aa1 + ab1, aa2 + ab2,..., aan + abn) [by distributivity in F]
= (aa1, aa2,..., aan) + (ab1,ab2,.....,abn)
= a(a1, a2,...., an) + a(b1, b2,...., bn)
= aα + aβ
Therefore scalar multiplication is distributive over vector addition in Fn.
V3. Scalar addition is distributive over scalar Multiplication :
Let a, b ∈ F and α ∈ Fn; then
(a + b) α = (a + b)(a,, a2 an)
= {(a + b) a1, (a + b) a2,.....,(a + b) an [by (2)]
= (aa1 + ba1, aa2 + ba2,....aan + ban) [by distributivity in F]
= (aa1, aa2,..., aan) + (ba1, ba2,......, ban)
= a (a1, a2,...., an) + b(a1, a2,...., an) [by (2)]
= aα + bα
Therefore addition is distributive over scalar multiplication in Fn
V4. Associativity for Scalar Multiplication:Let a,b ∈ F, then α ∈ Fn ;
(ab) α = (ab) (a1, a2,...., an)= (aba1, aba2,..., aban) [by (2)]
= a (ba1, ba2,......, ban) [by (2)]
= a {b(a1, a2,...., an)} [by (2)]
= a (bα)
Therefore scalar multiplication is associative in Fn
V5. Let I be the unity element of the field F, then for α ∈ Fn1α = 1 (a1, a2,...., an) = (1a1, 1a2,...., 2an) [by (2)]
= (a1, a2,...., an)
= α
From the above discussion, it is clear that Fn satisfies all the axioms for the vector space, therefore Fn(F) is a vector space.
Remarks:
- The above vector space is also expressed by Vn(F).
- If F = ℝ (Field of real number), then the corresponding vector space ℝn is called the Real Euclidean n space.
Similarly, ℂn is called the Complex Euclidean n space. - The set of all ordered pairs on F i.e. F2(F) = {( a1, a2) I a1, a2 ∈ f } is the vector space. Similarly the set of all ordered triads on F i.e. F3(F) = {(a1, a2, a3) I a1, a2, a3 ∈ F } is the vector space
These vector spaces are denoted by V2(F) and V3(F) respectively.
Example 3: The set M of all m * n real matrices (having their elements as real number) is a vector space over the field of real numbers with respect to addition of matrices and scalar multiplication of matrices.
Let M = {[aij]m*n |aij ∈ R} . If A, B ∈ M
where A = [aij]m*n ;B = [bij]m*n and a∈ℝ, then matrix addition and scalar multiplication in M are defined as follows :A + B= [aij] + [bij] = [aij+bij|]m*n ...(1)
and aA= a[aij] = [aaij]m*n ...(2)
Verification of space axioms:
V1. (M, +) is additive abelian group:
In Group theory, we have already seen that (M,+) is a commutative group where null matrix O mKn is the zero element and - A = [—aij] m*n ∈ M is the addictive inverse of any matrix A = [aij] ∈ M From the theory of matrices, following can be easily verified:
V2. Scalar Multiplication is distributive over vector additionV3. Scalar addition is distributive over Scalar Multiplication.
V4. Scalar Multiplication is associative.
V5. 1 is the unity element in ℝ, therefore every A ∈ M
1A = 1[aij] = [1aij] = [aij] = A
From the above discussion, it is clear that M(ℝ) is a vector space.
Example 4: The set V of all real valued continuous (differential or integral) function defined in a closed interval [0,1] is a vector space over the field ℝ of real numbers with addition and scalar multiplication of functions defined by:
(f + g ) ( x ) = f (x) + g (x) ∀ f , g ∈ V ; x ∈ [0,1] ..... (1)
(af)(x) = af (x) ∀ f ∈ V ,a ∈ ℝ ; x ∈ [0,1] .... (2)
Let V = (f I f :[0,1] → R is a continuous function}
From Calculus, we know that the sum of two continuous function is also a continuous function i.e. f ∈ V, g∈ V ⇒ (f + g) ∈ V
⇒ V is closed for addition of function defined above. Also we know that a ∈ ℝ ,f ∈ V af ∈ V ⇒ V is closed for scalar multiplication of function.
Verification of space axioms V (R):
V1. In group theory, we have already seen that (V, +) is an additive abelian group.V2. Scalar multiplication is distributive over vector addition:
Let f, g ∈ V and a ∈ ℝ. then
[a(f + g)](x) = a[(f + g)(x)] [by (2)]
= [a(f(x) + g(x))] [by (1)]
= af(x) + ag(x) [by distributivity in R]
= (af)(x) + (ag)(x) [by (2)]
= (af + ag)(x) ∀x ∈ [0,1] [by (1)]
⇒ a(f + g) = af + ag ,∀f ∈V and ∀a, b ∈ ℝV3. Scalar addition is distributive over Scalar Multiplication.
Let f ∈ V and a ,b ∈ ℝ , then
[(a + b)]f(x) = [(a + b)f(x)] [by (2)]
= [a f(x) + b f(x)] [by (1)]
V4. Scalar multiplication is associative :
Let a ,b ∈ ℝ and f ∈ V, then
[(ab)f](x) = (ab)f(x) [by (2)]
= a[(bf)(x)] [by (2)]
= [a(bf)](x) ∀ x ∈ [0,1] [by (2)]
Therefore scalar multiplication is associative in V.
V5. If unity 1 is real number and f ∈ V, then
(1f) (x) = 1 f(x) [by (2)]
= f(x) [v 1 is multiplicative identity in ℝ]
1 f = f [∀ f ∈ V]
From the above discussion, it is clear that V(ℝ) satisfies all the axioms for the vector space, therefore V(R) is a vector space.
Example 5: The set P(x) of all polynomials in one variable x over a field F is vector space over F with respect to addition of polynomials and multiplication of polynomials by an element of F.
The addition of polynomials and scalar multiplication in P(x) is defined as follows :
ifthen
...(1)
and..... (2)
We also know that if
p(x) = ∑ anxn ∈ P(x) and q(x) = ∑ bnxn ∈ P(x)
then p(x) + q(x) = S(an + bn)xn ∈ P(x) [ ∵ an ∈ F bn ∈ F ⇒ (an + bn) ∈ F ]
Again if a ∈ F,
then ap(x) = ∑(aan)xn ∈ P(x) [ ∵ a ∈ F , an ∈ F ⇒ aan ∈ F ]
Therefore P(x) is closed for the above defined addition and scalar multiplication operations.
Verification of space axioms in P(x):
V1. In the Ring theory, it has already been shown that (P(x), +) is an additive abelian group.
V2. Scalar multiplication is distributive over vector addition:[by (1)]
V3. Scalar addition is distributive over scalar multiplication:
Let a, b ∈ F and p(x) ∈ P(x), then
V4. Associativity for scalar multiplication:
Let a, b ∈ F and p(x) ∈ P(x), then
V5. If 1 is the unity element of the field F and p(x) ∈ P(x), then
From the above discussion, it is clear that P(x) satisfies all the axioms for the vector space, therefore P(x) is a vector space.
Example 6: The set ℝ+ of positive real numbers is a vector space over the field ℝ of real numbers for the operations Vector addition’ ⊕ and ‘scalar multiplication'
defined as follows:
Since the product of two positive real numbers is definitely a positive number i.e.,
Also every real power of a positive number is always positive real,
Therefore ℝ+ is closed for the above defined vector addition (and scalar multiplication).
Verification of a space axioms in R+(R):
V1. It can be easily see thatis an additive abelian group,
for 1 ⊕ x = x ⊕ 1, x1 = x [∵ x1 = x, ∀ x ∈ ℝ+]
and for every x ∈ ℝ+, there exist 1/x ∈ ℝ+ such that
V2. Scalar multiplication is distributive over vector addition:
Let x, y ∈ ℝ+ and a ∈ ℝ, then
V3. Distributivity on scalar addition:
Let a, b ∈ ℝ and x ∈ ℝ, then
V4. Scalar multiplication is associative:
Let a, b ∈ ℝ and x ∈ ℝ+, then
V5.
From the above discussion, it is clear that ℝ+ satisfies all the axioms for the vector space, therefore ℝ+(ℝ) is a vector space.
General properties of Vector Space
If V be the vector space over the field F and 0 ∈ V be its zero vector, then the following properties are obvious because of V being an abelian group :
(i) For any α ∈ V, α + β = α β = 0 [Uniqueness of the zero element]
(ii) α ∈ V , β ∈ V , a + β = 0 = > β = - α [Uniqueness of inverse]
(iii) For any α, β, γ ∈ V , α + β = α + γ = > β = γ [cancellation law]
Now we shall establish few more properties of V :
Theorem: Let V be a vector space over a field F. If 0 be the zero vector in V and 0 be the additive identity in F, then
(i) a 0 = 0, ∀ a ∈ F
(ii) 0α = 0, ∀ α ∈ V
(iii) a(-α) = -(aα), ∀ a ∈ F, a ∈ V
(iv) (-a)α = -(aα), ∀ a ∈ F, a ∈ V
(v) a(α - β) = aα - αβ, ∀ a ∈ F, α, β ∈ V
(iv) For any a ∈ F, α ∈V
aα = 0 a = 0 or α = 0
Proof,
(i) ∵ 0 zero element in V, therefore 0 + 0 = 0
⇒ a(0 + 0) = a0 V a ∈ F
⇒ a0 + a0 = a0 ...... [by V2]
⇒ a0 + a0 = a0 + 0 ...... [∵ 0 is zero element in V]
⇒ a0 = 0
(ii) ∵ 0 ∈ F is additive identity in F, therefore
0 + 0 = 0
⇒ (0 + 0)α = 0α ∀ a ∈ V
⇒ 0α+ 0α = 9α ...... [by V3]
⇒ 0α + 0α = 0α + 0 ...... [∵ 0 is zero element in V]
⇒ 0α = 0 [cancellation law in V]
(iii) For any a ∈ F and a ∈ V
a[α + (-α) = aa + a(-α) ...... [by V2]
⇒ a0 = aα + a(-α)
⇒ 0 = aα + a(-α) ...... [by (1)]
⇒ a(-α) is additive inverse of aa
⇒ a (-α) = -(aα)
(iv) For any a ∈ F and α ∈ V
[a + (-a)]α = aa + (-a)α ...... [by V3]
⇒ 0a = aα + (-a)α
⇒ 0 = aα + (-a)α ....... [by (ii)]
⇒ (-a)α is additive inverse of aa
⇒ (-a)α = -(aα)
(v) For any a ∈ F and α, β ∈ V
a(α - β) = a[α + (-p)]
= aα + a(-β) .......[by V2]
= aα + [-(aβ)] ...... [by (iii)]
= aα - aβ
(vi) Let a ∈ F and α ∈ V such that a ≠ 0 and aα = 0
Now since multiplicative inverse of every non zero element exist in F,
therefore a ∈ F, a ≠ 0 ⇒ a-1 ∈ F
aα = 0 => a-1 (aα) = a-1 0
⇒ (a-1a)α = 0 . .......[by V4 and (i)]
⇒ 1α = 0
⇒ α = 0 ......[by V5]
Again let aα = 0 and α ≠ 0, then to prove that a = 0.
If possible, let a ≠ 0, then a-1 ∈ F
aα = 0 ⇒ a-1(aα) = 0
⇒ (a-1a)α = 0
⇒ 1α = 0
⇒ α = 0
which is contrary to the assumption α ≠ 0, therefore a = 0.
Hence aα = 0 ⇒ a = 0 or α = 0
Example 7: Let V(F) be a vector space, then :
(i) For any a, b ∈ F and a ∈ V, a ≠ 0,
aα = bα ⇒ a = b
(ii) For any α, β ∈ V and a ∈ F, a ≠ 0
aα = aβ ⇒ α = β
(i) aα = bα ⇒ aα - b α = 0
(a - b)α = 0 .... [by V3]⇒ [a + (-b)]α = 0
⇒ a + (-b) = 0 [∵ α ≠ 0]
[by theorem (vi)]
⇒ a = -(-b) [by additive inverse]
⇒ a = b
(ii) aα = aβ => aα - aβ = 0⇒ a(α - β) = 0 [by V2]
⇒ α - β = 0 [∵ a ≠ 0, therefore by theorem (vi)]
⇒ α = β
Example 8: If V(F) is a vector space, then prove that: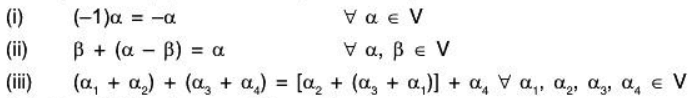
(i) By theorem (iv), we have
(ii)
(iii)
Example 9: Let V be the set of all ordered pairs of real numbers and F be the field of real numbers. Examine whether V(F) is a vector space or not for the following defined operations :
(a) (a, b) + (C, d) = (0, b + d); P(a, b) = (pa, pb)
(b) (a, b) + (C, d) == (a + c, b + d); P(a, b) = (0, pb)
(c) (a, b) + (C, d) == (a + c, b + d); P(a, b) = (p2 a, p2 b)
(d) (a, b) + (C, d) == (a, b); P(a, b) = (pa, pb)
(e) (a, b) + (C, d) == (a + c, b + d); P(a, b) = (I p I a, I p I b) ∀ a, b, c, d, p ∈ ℝ
(a) It can be easily seen that the additive identity for the defined vector addition does not exist. If suppose any element (c, d) ∈ V is taken as additive identity for vector addition, then
(a, b) + (c, d) = (0, b + d) * (a, b)
Therefore (V, +) is not an abelian group.Consequently V(F) is not a vector space.
(b) In this case, (V, +) is an abelian group but space axiom V5 is not satisfied, because
1(a, b) = (0, 1b) = (0, b) ≠ (a, b)
Therefore V(F) is not a vector space.
(c) In this case, (V +) is an abelian group but space axiom V3 is not satisfied, because
Therefore V(F) is not a vector space.
(d) In this case the defined vector addition is not commutative, because for
(a, b); (c, d) ∈ V
(a, b) + (c, d) = (a, b)
and (c, d) + (a, b) = (c, d)
(a, b) + (c, d) ≠ (c, d) + (a, b)
Therefore (V, +) is not an abelian group.Consequently, V(F) is not a vector space.
(e) In this case, (V, +) is an abelian group but space axiom V3 is not satisfied, because
(p + q)(a, b) = (I p + q I a, I p + q I b) p, q ∈ ℝ
≠ (I p I a, I p I b) + (I q I a, I q I b) [ ∵ l p + q l ≠ lp l + l q l , p, q ∈ ℝ]
⇒ (p + q)(a, b) ∈ p(a, b) + q(a, b)
Therefore V(F) is not a vector space.
Theorem: Let V be a vector space over a field K.
(i) For any scalar k ∈ K and 0 ∈ V, k0 = 0.
(ii) For 0 ∈ K and any vector u ∈ V, 0u = 0.
(iii) If ku = 0, where k ∈ K and u ∈ V, then k = 0 or u = 0.
(iv) For any k ∈ K and any u ∈ V, (- k)u = k(- u) = - ku.
Examples of Vector Spaces
Space Kn
Let K be an arbitrary field. The notation Kn is frequently used to denote the set of all n-tuples of elements in K. Here Kn is a vector space over K using the following operations :
(i) Vector Addition: 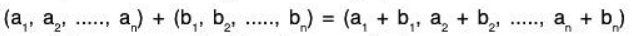
(ii) Scalar Multiplication:
k(a1, a2, ..... an) = (ka1, ka2,........., kan)
The zero vector in Kn is the n-tuple of zeros,
0 = (0, 0, .... , 0)
and the negative of a vector is defined by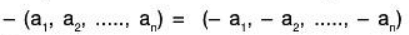
Polynomial Space
P(t) Let P(t) denote the set of all polynomials of the form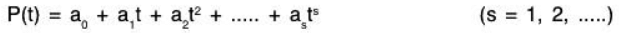
where the coefficient a, belong to a field K. Then P(t) is a vector space over K using the following operations:
(i) Vector Addition: Here p(t) + q(t) in P(t) is the usual operation of addition of polynomials.
(ii) Scalar Multiplication: Here kp(t) in P(t) is the usual operation of the product of a scalar k and a polynomial p(t).
The zero polynomial 0 is the zero vector in P(t).
Vector Subspaces
Let V(F) be a vector space and W ⊂ V. We have also seen that the set W is closed for the binary operation +, if for any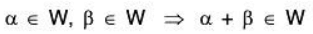
and in that case restriction of + to W is a binary operation in W.
Similarly we say that a subset W of vector space V(F) is closed for the external composition if for any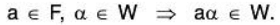
In such a case the restriction of the mapping of F * V to F * W is a mapping from F * W to W and is therefore an external composition for W. We shall therefore say that W is closed for the external composition in V, then external composition in V induces an external composition in W. If W itself be a vector space for these induced compositions, then we say that W is a subspace of V.
Definition: Let V(F) be a vector space. A non void subset W of V is a subspace of V, if W itself is a vector space over F for the restrictions to W of the addition and multiplication by scalar defined for V.
Improper or Trivial subspaces
Every vector space V(F) has atleast two subspaces viz,
(i) V itself
(ii) {0} zero vector space
These space are called Improper subspaces.
Proper subspaces: The subspaces other than the improper subspaces are called proper subspaces.
Example: The set of real numbers  is a subspace of the vector space
is a subspace of the vector space 
Example: The set 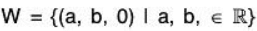 is a subspace of the vector space
is a subspace of the vector space 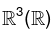 .
.
Criteria for a Subspace
Theorem: The necessary and sufficient conditions for a non void subset W of a vector space V(F) to be a subspace of V(F) is that W is closed under vector addition and scalar multiplication:
i.e., α g W, β g W ⇒ α + β ∈ W ...(1)
a ∈ F, β ∈ W ⇒ aα ∈ W ...(2)
Proof.
The condition is necessary (⇒): Let W be a non empty subspace of V(F). By definition of subspace W itself is also a vector space over F wrt vector addition and scalar multiplication in V. So it implies that W is closed wrt these two binary compositions.
The condition is sufficient (⇐): Let W be closed for vector addition and scalar multiplication i.e. (1) and (2) hold. Now we have to prove that W is a subspace of V(F).
∵ W ≠ φ, therefore let α ∈ W and 1 ∈ F be unity element of the field F.
∵ 1 ∈ F ⇒ - 1 ∈ F
∴ -1 ∈ F, α ∈ W
Therefore every element of W has its additive inverse in W.
Now α ∈ W, -α ∈ W
Therefore zero vector of V is also the zero vector of W.
Since the elements of W are also the elements of v, therefore they also obey the commutative as well as associative laws as are true in V.
Therefore (W, +) is an abelian group.
Moreover V being the vector space satisfies remaining axioms V2, V3, V4, V5 so is in W and W is a subset of V.
Therefore W is a subspace of the vector space V(F).
Theorem: The necessary and sufficient conditions for a non void subset W of a vector space V(F) to be a subspace of V(F) are:
Proof.
The condition is necessary (⇒) :
Let W be a subspace of V(F). Then W itself is also a vector space wrt the operations defined for V. Therefore (W, +) is also an abelian group.
Consequently,
Therefore the condition (i) is necessary.
Again W is closed for the scalar multiplication, being subspace of V. Therefore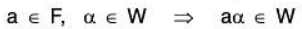
Therefore the condition (ii) is also necessary.
The condition is sufficient (⇐) :
Now let W be a non empty subset of V(F) which satisfies the given conditions, then to prove that W is a subspace of V(F).
∵ W ≠ φ, therefore let α ∈ W, then by condition (i)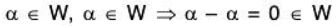
Therefore zero vector of V is also the zero vector of W.
Again by condition (i),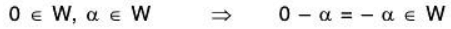
Therefore additive inverse of each element exist in W.
Now α ∈ W, β ∈ W ⇒ α ∈ W, -β ∈ W
⇒ α - (-β) ∈ W [by condition (i)]
⇒ (α + β) ∈ W
Therefore W is closed for vector addition.
Since W ⊂ V and vector addition is associative and commutative in V, so also in W
Hence (W, +) is an abelian group.
Again by condition (ii), W is closed for the scalar multiplication and W ⊂ V , therefore W will also satisfy remaining axioms V2, V3, V4, V5. Consequently, W is a subspace of V(F).
Theorem: The necessary and sufficient condition for a non void subset W of a vector space V(F) to be a subspace of V(F) is:
a, b ∈ F and α, β ∈ W ⇒ (aα + bβ) ∈ W
Proof: The condition is necessary (⇒ ):
Let W be a subspace of V(F). Then W will be closed for the scalar multiplication. Therefore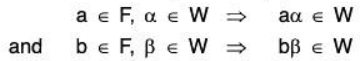
Again, We being subspace, will be closed for the vector addition, therefore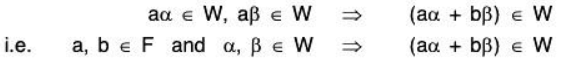
Therefore the given condition is necessary.
The condition is sufficient (⇐): Now let W be a non empty subset of V(F) which satisfy the given conditions. Taking a = 1, b = 1, then by the given condition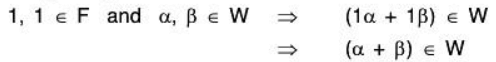 [by V5]
[by V5]
Therefore W is closed for the vector addition.
Now taking a = -1, b = 0, then again by the given condition
Therefore additive inverse of each element exist in W.
Finally, taking a = 0, b = 0, then by the given condition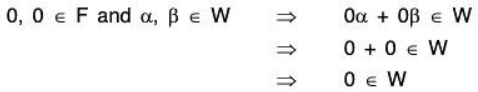
Therefore zero vector of V also exists in W.
Since W ⊂ V and vector addition is associative and commutative in V, so is in W also.
Hence (W, +) is an abelian group.
Again taking b = 0, we see that if a ∈ F and α, β ∈ W, then by the given condition
a, 0 ∈ F and α, β ∈ W
Therefore W is closed for the scalar multiplication. But W ⊂ V, therefore W will satisfy the remaining axioms V2, V3, V4, V5.
Consequently W is a subspace of V(F).
Intersection of two subspaces
Theorem: The intersection of two subspaces W1 and W2 of vector space V(F) is also a subspace of V(F).
Proof: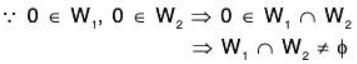
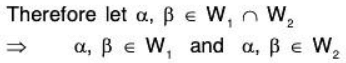
Since W1, and W2 are subspaces, therefore for any a, b ∈ F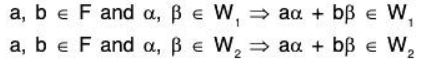
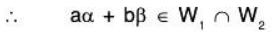
Therefore a, b ∈ F and α, β ∈ W1 ∩ W2 ⇒ aα + bβ ∈ W1 ∩ W2
⇒ W1 ∩ W2 is also a subspace of V(F).
Generalisation: The intersection of an arbitrary family of subspaces of a vector space is also a subspace.
Proof: Let V(F) be a vector space and { W1, W2, ...} be a family of its subspace, then to prove that ∩ Wi is also a subspace of V(F).
Now since every W is a subspace of V(F), therefore for any a, b ∈ F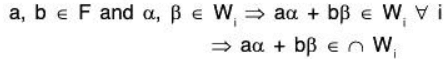
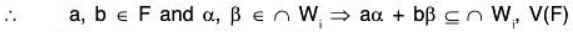
⇒ ∩ Wi is also a subspace of V(F).
Union of two subspaces
The union of two subspaces of a vector space V(F) is not necessarily a subspace of V(F). This result can be proved with the help of the following counter example:
if 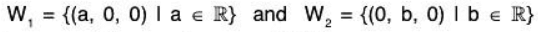
are subspaces of the vector space 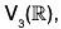
but their union
W1 ∪ W2 = {α I α = (a, 0, 0) or (0, b, 0)}
is not subspace of 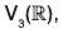 because if
because if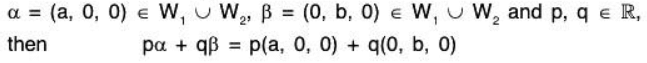
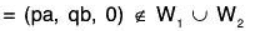
Theorem: The union of two subspaces W1 and W2 of a vector space V(F) is a subspace iff either W1 ⊂ W2 or W2 ⊂ W1
Proof: Let W1 and W2 be the subspaces of a vector space V(F) such that
W1 ⊂ W2 or W2 ⊂ W1, then
W1 ⊂ W2 or W2 ⊂ W1 ⇒ W1 ∪ W2 = W1 or W1
But W1 and W2 are subspaces, therefore W1 ∪ W2 will also be a subspace.
Conversely:
Let W1 ∪ W2 be the subspace of the vector space V(F).
Also suppose that 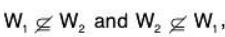 then there exist α1,α2 ∈ V such that
then there exist α1,α2 ∈ V such that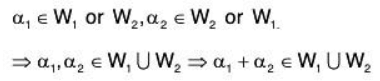
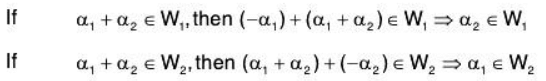
Hence W1 ⊆ W2 or W2 ⊂ W1
Example 10: Prove that the set W = {(a, b, 0) I a, b ∈ F} is a subspace of the vector space V3(F).
∵ V3(F) = {(a, b, c) I a, b, c ∈ F} and W = {(a, b, 0) I a, b ∈ F}
Therefore, clearly W ⊂ V3 (F).
Let α = (a1, b1, 0) and p = (a2, b2, 0) be any two elements of W and p, q ∈ F, then
Therefore p, q ∈ F and α, β ∈ W ⇒ pα + qβ ∈ W
Therefore W is a subspace of the vector space V3(F).
Example 11: Show that the set W = {(a, b, c) I a - 3b + 4c = 0; a, b, c ∈ R} of 3-tuples is a subspace of the vector space V3(ℝ)
∵ V3(ℝ) = {(a, b, c) I a, b, c ∈ ℝ}
and W = {(a, b, c) I a - 3b + 4c = 0; a, b, c ∈ ℝ} therefore, clearly W ⊂ V3(ℝ)
Let.....(1)
Now if, p, q ∈ ℝ, thenTherefore p, q ∈ ℝ and α, β ∈ W ⇒ pα + qβ ∈ W
∴ W is a subspace of the vector space V3(ℝ).
Example 12 : Examine which of the following sets is a subspace of the vector space V3(ℝ).
(a) W1 = {(x, 2y, 3z) I x, y, z ∈ ℝ}
(b) W 2 = {(x, x, x) I x ∈ ℝ )
(c) W 3 = {(x, y, z) I x, y, z ∈ ℚ }
∵ V3(ℝ) = {(x, 2y, 3z) I x, y, z ∈ ℝ}
Therefore observing 3-tuples of W1, W2, W3 and V3(ℝ), it is clear that
(a) Let α = (x1, 2y1, 3z1) ∈ W1 and β = (x2, 2y2, 3z2) ∈ W1
where x1, x2, y1, y2, z1, z2 are all real numbers.
if a, b ∈ R, then
∴ a, b ∈ R and α, β ∈ W1 ⇒ aα + bβ ∈ W
Therefore W1 is a subspace of the vector space V3(ℝ).
(b) let
where x1, x2 ∈ ℝ. If a, b ∈ ℝ, then
Therefore W2 is a subspace of the vector space V3(ℝ).
(c) Let a = (3, 5, 4) ∈ W3 then for a = √2 ∈ ℝ
Consequently, W3 is not closed for the scalar multiplication.
Therefore W3 is not a subspace of the vector space V3(ℝ).
Example 13: If V(F) is a vector space of all n * n matrices over the field F, then prove that the set W of all n x n symmetric matrices over F will be a subspace of V(F).
Clearly W is a non empty subset of V(F), W = (A : AT = A, A ∈ V}.
Let A, B ∈ W ⇒ AT = A and BT = B [being symmetric] ...(1)
If a, b ∈ F, Then aA ∈ V, bB ∈ V ⇒ aA + bB ∈ V
and⇒ aA + bB is a symmetric matrix⇒ (aA + bB) ∈ W
a, b ∈ F and A, B ∈ W ⇒ aA + bB ∈ W
Therefore W is a subspace of V(F).
Example 14: If M2(F) is a vector space of all 2 x 2 matrices over the field F, then prove that the set W of all matrices of the form 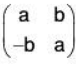 over F will be a subspace of M2(F).
over F will be a subspace of M2(F).
Let
and p ∈ F, then
Therefore W is closed for the vector addition and scalar multiplication in M2(F) Hence M2(F) is a subspace.
Example 15: If a1, a2, a3 are fixed elements of a field F; then prove that the set W = {(x1, x2, x3) I x1, x2, x2 ∈ F; a1x1 + a2x2 + a3x3 = 0} is a subspace of the vector space V3(F).
Let α = (x1, x2, x3) ∈ W and b = (y1, y2, y3) ∈ W
and a1x1 + a2x2 + a3x3 = 0 and a1y1 + a2y2 + a3y3 = 0 ...(1)
If a, b ∈ F, then(by the properties of the field F)= a0 + b0
= 0 + 0 = 0 ...(3)
Therefore by (2) and (3),
aα + bβ = (ax1 + by1, ax2 + by2, ax3 + by3) ∈ W
Therefore W is a subspace of V3(F).
Example 16: Let V(F) be a vector space of all polynomials of degree n in an indeterminate x, then prove that the set S of all polynomials of degree ≤ n over F is a subspace of V(F) where n is an arbitrary positive integer.
Let f(x), g(x) ∈ S, so that f(x) and g(x) are polynomials over F of degree ≤ n. Now if a and b are any scalars ∈ F, then af(x) + bg(x) will also be a polynomials of degree ≤ n.
Thus f(x), g(x) ∈ S and a, b ∈ F ⇒ af(x) + bg(x)
Hence S is a subspace of V.
Example 17: Let S be the set of all solutions (x, y, z) satisfying the simultaneous equations ax + by + cz = 0 and dx + ey + fz = 0 ; a, b . c, d, e, f ∈ ℝ. Thus S is a subspace of ℝ3 over ℝ.
If (x1, y1, z1) and (x2, y2, z2) be solutions of the given equations,

Hence if (x1, y1, z2) ∈ V, (x2, y2, z2) ∈ V, then (x1 + x2, y1 + y2, z1 + z2) is also in V.
Similarly a(ax1) + b(αy1) + c(αz1) = (aαx1 + bαy1 + cαz1)
Hence S is a subspace of ℝ3 over ℝ.
Example 18: Examine which of the following sets of vectors α = (a1, a2,....., an) in ℝn are subspaces of ℝn ? (n ≥ 3)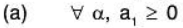
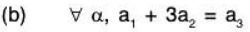
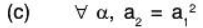
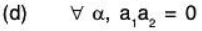
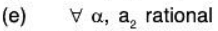
(a) Let
Again letand b = (b1, b2,...... bn) ∈ W1,
then by the given condition a1 ≥ 0, b1 ≥ 0.Now for a, b ∈ ℝ
But aa1 + bb1 is not necessarily non-negative,
for example If we take a = -2, b = -1, then for a, = 4, b = 3
aa1 + bb1 = (-2 )4 + (-1 )3 = -11 < 0
Therefore aα + bβ ∉ W,. Hence W1 is not a subspace.(b) Let W2 = {α I α ∈ ℝn and a1 + 3a2 = a3}
Again let α = (a1, a2, ..., an) ∈ W2 and β= (b1, b2, ..., bn) ∈ W2
Then by the given condition
a1 + 3a2 = a3 and b, + 3b2 = b3 ...(1)
Now for a, b ∈ ℝ
= aa3 + bb3 [by (1)]
a, b ∈ ℝ and α, β ∈ W2 ⇒ aα + gβ ∈ W2
Therefore W2 is a subspace of .(c) Let
Again let α = (a1, a2, ..., an) ∈ W3 and β = (b1, b2, ..., bn) ∈ W3
Then by the given condition,Now for a, b ∈ ℝ
But the square of (aa1 + bb1) is not necessarily (aa2 + bb2).
for example When a2 = 4, a1 = 2, b2 = 9, b1 = 3, a = 2, b = -2,
then aa2 + bb2 = 8 - 18 = - 10 when (aa1 + bb1)2 = (4 - 6)2 = 4.
thereforeHence W3 is not a subspace of ℝn.
(d) Let
Again let α = (a1, a2, ..., an) ∈ W4 and β = (b1, b2, ..., bn) ∈ W4
Then by the given condition a1a2 = 0 and b1b2 = 0.Now for a, b ∈ ℝ
But (aa1 + bb1) (aa2 + bb2) is not necessarily zero,
for example Taking a1 = 0, a2 = 2, b1 = 1, b2 = 0, a = 2, b = 3
(aa1 + bb1)(aa2 + bb2) = (0 + 3)(4 + 0) = 12 * 0
Therefore aα + bβ ∈ W4. Hence W. is not a subspace of ℝn.
(e) LetAgain let α = (a1, a2, ..., an) ∈ W5 and β = (b1, b2, ..., bn) ∈ W4
Then by the given condition a2 b2 are rational numbers.Now for a, b ∈ ℝ
But aa2 + bb2 is not necessarily a rational number.for example
If we take a = √2, b = √3, a2 = 3, b2 = 4
aa2 + bb2 = 3√2 + 4√3 which is not rational
Therefore aα + bβ ∉ W5. Hence W5 is not a subspace of ℝn.
|
98 videos|27 docs|30 tests
|
FAQs on Vector Space & Linear Transformation - 1 - Mathematics for Competitive Exams
| 1. What is a vector space and how is it related to linear transformations? |  |
| 2. How are vector spaces and linear transformations used in the IIT JAM exam? |  |
| 3. What are the properties that a set of vectors must satisfy to form a vector space? |  |
| 4. How can one determine if a linear transformation is invertible? |  |
| 5. How are linear transformations represented using matrices? |  |

|
Explore Courses for Mathematics exam
|

|
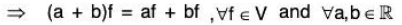
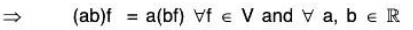


 then
then ...(1)
...(1) ..... (2)
..... (2)
 [by (1)]
[by (1)]





 defined as follows:
defined as follows:


 is an additive abelian group,
is an additive abelian group,




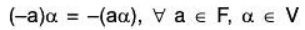
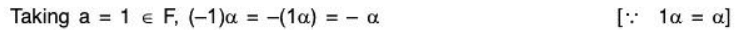
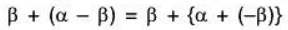

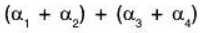

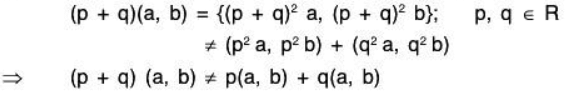



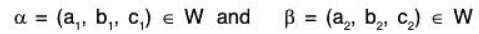
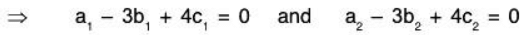
 .....(1)
.....(1)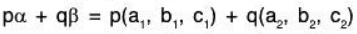
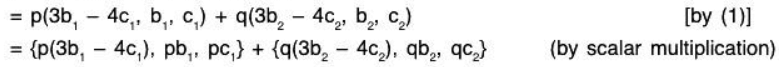

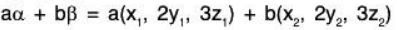
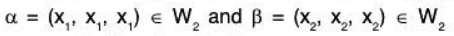
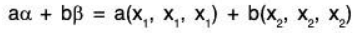
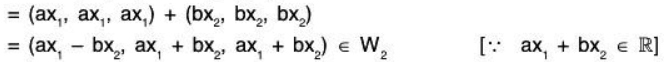
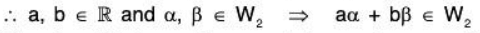

 ⇒ aA + bB is a symmetric matrix⇒ (aA + bB) ∈ W
⇒ aA + bB is a symmetric matrix⇒ (aA + bB) ∈ W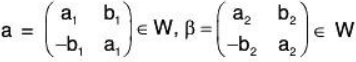
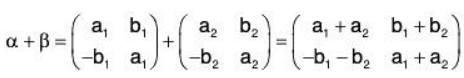
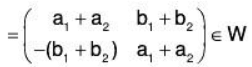
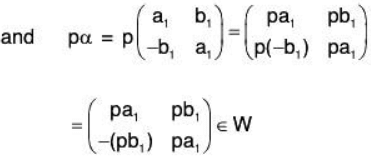
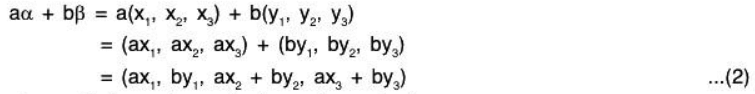
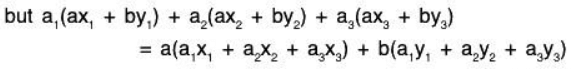 (by the properties of the field F)= a0 + b0
(by the properties of the field F)= a0 + b0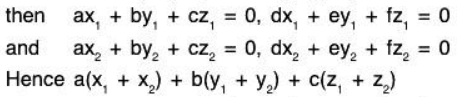
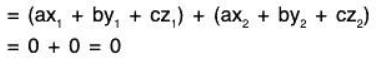
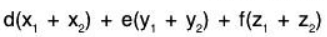
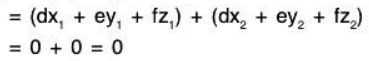
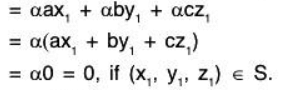
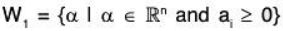
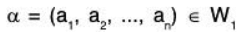 and b = (b1, b2,...... bn) ∈ W1,
and b = (b1, b2,...... bn) ∈ W1, 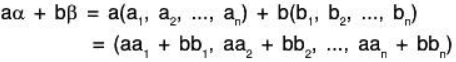
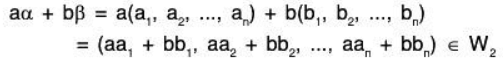
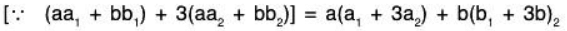
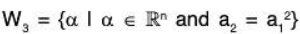 Again let α = (a1, a2, ..., an) ∈ W3 and β = (b1, b2, ..., bn) ∈ W3
Again let α = (a1, a2, ..., an) ∈ W3 and β = (b1, b2, ..., bn) ∈ W3 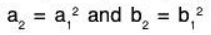 Now for a, b ∈ ℝ
Now for a, b ∈ ℝ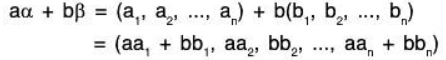
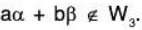 Hence W3 is not a subspace of ℝn.
Hence W3 is not a subspace of ℝn.