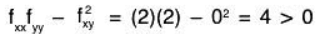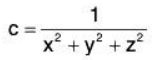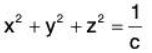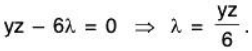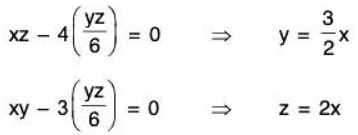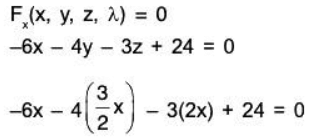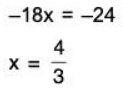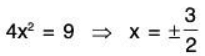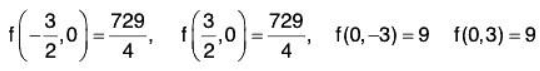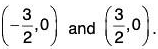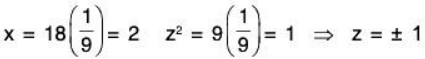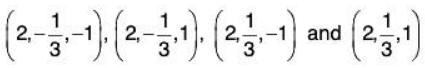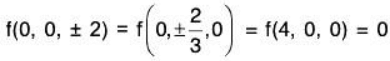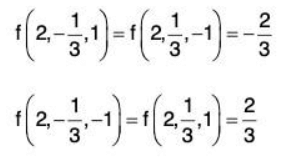Functions of Two or Three Variables- II | Mathematics for Competitive Exams PDF Download
Maxima and Minima of Functions of Two Variables
Reminder
For a function of one variable f(x), we find the local maxima/minima by differentiation. Maxima/ minima occur when f’(x) = 0.
- x = a is a maximum if f'(a) = 0 and f"(a) < 0;
- x = a is a minimum if f'(a) = 0 and f"(a) > 0;
A point where f”(a) = 0 and f”'(a) ≠ 0 is called a point of inflection. Geometrically, the equation y = f(x) represents a curve in the two-dimensional (x,y) plane, and we call this curve the graph of the function f(x).
Functions of two variables
Our aim is to generalise these ideas to functions of two variables. Such a function would be written as z = f(x,y)
where x and y are the independent variables and z is the dependent variable. The graph of such a function is a surface in three dimensional space. A simple example might be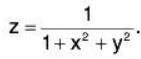
z is the height of the surface above a point (x,y) in the X-Y plane.
For functions z = f(x,y) the graph (i.e. the surface) may have maximum points or minimum points (or both). But for surfaces there is a third possibility - a saddle point.
A point (a,b) which is a maximum, minimum or saddle point is called a stationary point. The actual value at a stationary point is called the stationary value. What we need is a mathematical method for finding the stationary points of a function f(x,y) and classifying them into maximum, minimum or saddle point. This method is analogous to, but more complicated than, the method of working out first and second derivatives for functions of one variable.
Let’s remind about partial derivatives. The sort of function we have in mind might be something like.
f(x,y) = x2y3 + 3y + x
and the partial derivatives of this would be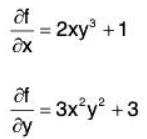
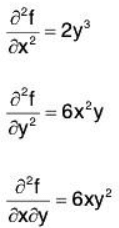

Note that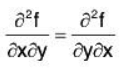
This is true for any well behaved function. In terms of notation, we will frequently use the other, subscript, notation for partial derivatives: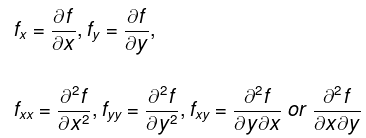
Finding stationary points
To find the stationary points of f(x,y), work out 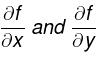 and set both to zero. This gives you two equations for two unknowns x and y. Solve these equations for x and y (often there is more than one solution, as indeed you should expect. After all, even functions of one variable may have both maximum and minimum points).
and set both to zero. This gives you two equations for two unknowns x and y. Solve these equations for x and y (often there is more than one solution, as indeed you should expect. After all, even functions of one variable may have both maximum and minimum points).
Classifying stationary points
The procedure for classifying stationary points of a function of two variables is analogous to, but somewhat more involved, than the corresponding ‘second derivative test’ for functions of one variable. Below is, essentially, the second derivative test for functions of two variables:
Let (a,b) be a stationary point, so that fx = 0 and fy = 0 at (a, b). Then:
- if
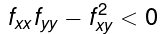 at (a,b) then (a,b) is a saddle point.
at (a,b) then (a,b) is a saddle point. - if
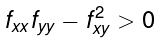 at (a, b) then (a,b) is either a maximum or a minimum.
at (a, b) then (a,b) is either a maximum or a minimum.
Distinguish between these as follows:
- if fxx < 0 and fyy < 0 at (a,b) then (a,b) is a maximum point
- if fxx > 0 and fyy > 0 at (a,b) then (a,b) is a minimum point
if 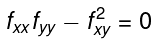 then anything is possible. More advanced methods are required to classify the stationary point properly.
then anything is possible. More advanced methods are required to classify the stationary point properly.
Let's give some idea where the above conditions come from. It is all based on Taylor’s theorem for a function of two variables. Taylor’s theorem for a function of one variable i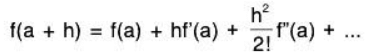
For a function of two variables Taylor’s theorem is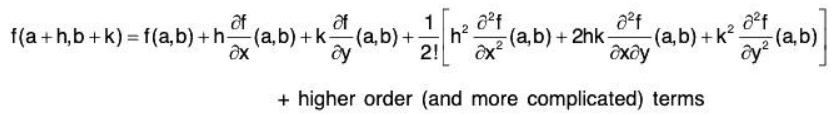 The higher order terms can be neglected in straightforward cases. Lets suppose (a,b) is a maximum point. Then fx = 0 and fy = 0 at (a,b) and, because (a,b) is a local maximum the function must x y be smaller at neighbouring points, i.e. when h and k are sufficiently small, f(a + h, b + k) < f(a, b)
The higher order terms can be neglected in straightforward cases. Lets suppose (a,b) is a maximum point. Then fx = 0 and fy = 0 at (a,b) and, because (a,b) is a local maximum the function must x y be smaller at neighbouring points, i.e. when h and k are sufficiently small, f(a + h, b + k) < f(a, b)
But from Taylors theorem, neglecting higher order terms and noting that the first derivative terms are zero at (a.b),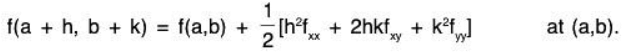
However f(a + h, b + k) < f(a, b), hence
h2fxx + 2hkfxy + k2fyy < 0 at (a,b)
for all small values of h and k. Dividing by k2 gives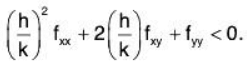
Let ξ = h/k. Then even though h and k are both small, ξ doesn’t have to be small.
So we have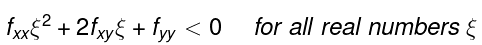
Thus we have a quadratic expression that is negative for all values of its variable ξ (and so, in particular, has no roots). A few graphs will show that this is only possible if fxx< 0, fyy < 0 and 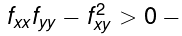 the latter condition is the one to do with having no roots. All these inequalities hold at (a,b).
the latter condition is the one to do with having no roots. All these inequalities hold at (a,b).
Similar analysis yields the conditions under which a stationary point is a minimum or saddle point.
Definition
- A function f(x, y) is said to have a maximum at a point (a, b) if there exists a nbd. N of (a, b) such that
f(a + h, b + k) < f(a, b) ∀ (a + h, b + k) ∈ N ~ {(a, b)}.
The set N ~ {a, b)} is called a deleted nbd. of (a, b). - A function f(x, y) is said to have a minimum at a point (a, b) if there exists a nbd. N of (a, b) such that
f(a + h, b + k) > f(a, b) ∀ (a + h, b + k) ∈ N ~ {(a, b)}. - A function f(x, y) is said to have an extremum at a point (a, b) if it has either a maximum or minimum at (a, b).
Theorem: If a function f(x, y) has an extremum at any point (a, b) of the domain of f and if f admits of partial derivatives fx and fy at (a, b),
then fx(a,b) = 0 and fy(a, b) = 0.
Proof: Suppose f(x, y) has a maximum at (a, b). Then the function f(a, b) of a single variable x must have a maximum at x = a and so
fx(a, b) = 0 when x = a i.e., fx(a, b) = 0.
Again the function f(a, y) of a single variable y must have a maximum at y = b and so fy(a, y) = 0 when y = b i.e., fy(a, b) = 0.
Exactly similar is the case when f has a minimum at (a, b). - A point (a, b) is said to be a critical point for a function f(x, y) if fx and fy both exist at (a, b) and fx(a, b) = 0, fy(a, b) = 0.
If (a, b) is a critical point for a function f(x, y), then f(a, b) is called a stationary value of f.
Example 1: Find the maxima and minima of the function
f(x, y) = x3 + y3 - 3x - 12y + 20.
We have
fx = 3x2 - 3, fy = 3y2 - 12, fxx = 6x, fyy = 6y, fxy = 0.
To determine the critical points, we solve
fx = 0, fy = 0 ⇒ 3x2 - 3 = 0, 3x2 - 12 = 0
⇒ x = ± 1, y = ± 2. Hence the critical points are (1,2), (1-2), (-1,2), (-1,-2).At (1,2),
A = fxx = 6 > 0, B=0, C=12.
AC - B2 = fxx. fyy - (fxy)2 = 6 x 12 - 0 = 72 > 0.
Thus f has minimum at (1, 2).At (1,-2),
AC - B2 = -6 * (-12) - 0 < 0.
Thus f has neither maximum nor minimum at (1, -2).At (-1,2),
AC - B2 = -6 * 12 - 0 < 0.
Thus f has neither maximum nor minimum at (-1, 2).
At (-1,-2), A = - 6 < 0,
AC - B2 = (-6)(-12) - 0 > 0.
Thus f has maximum at (-1, -2).
Example 2: Lets work out the stationary points for the function f(x,y) = x2 + y2 and classify them into maxima, minima and saddles.
We need all the first and second derivatives so lets work them out. we have
fx = 2x
fy = 2y
fxx = 2fyy= 2
fxy = 0For stationary points we need fx = fy = 0. This gives 2x = 0 and 2y = 0 so that there is just one stationary point, namely (x.y) = (0,0). We now need to classify it.
Nowso it is either a max or a min. But fxx = 2 > 0 and fyy = 2 > 0. Hence it is a minimum. Our conclusion is that this function has just one stationary point (0, 0) and that it is a minimum.
Example: 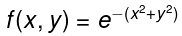
The first and second order partial derivatives of this function are: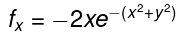
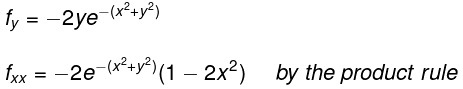
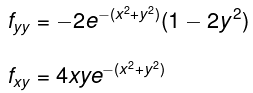
Stationary points are when fx = 0 and fy = 0 and so there is only one stationary point, at (x,y) = (0, 0). Substituting (x.y) = (0,0) into the expressions for fxx , fyy and fxy gives
fxx = -2, fyy = -2, fxy = 0
Therefore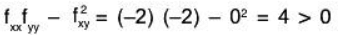
So that (0,0) is either a min or a max. Since fxx < 0 and fyy < 0 it is a maximum.
Example: f(x,y) = 2 - x2 - xy - y2
For this function
fx= - 2x - y
fy = -x -2y
fxx = -2
fyy= -2
fxy = -1
For stationary points, -2x - y = 0 and -x - 2y = 0 so again the only possibility is (x, y) = (0,0). We have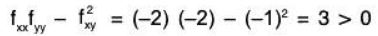
so that (0, 0) is either a max or a min. Since fxx < 0 and fyy < 0, So it is a maximum.
Functions of Three Variables
We extend our study of multivariable functions to functions of three variables.
Definition: Function of Three Variables. Let D be a subset of ℝ3. A function f of three variables is a rule that assigns each triple (x, y, z) in D a value w = f(x, y, z) in ℝ . D is the domain of f; the set of all outputs of f is the range.
Note how this definition closely resembles that of Function of two variables.
Example 1: Let 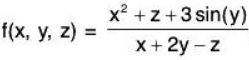 . Evaluate f at the point (3, 0, 2) and find the domain and range of f.
. Evaluate f at the point (3, 0, 2) and find the domain and range of f.
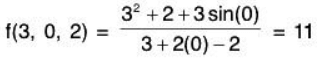
As the domain of f is not specified, we take it to be the set of all triples (x, y, z) for which f(x, y, z) is defined. As we cannot divide by 0, we find the domain D is D = {(x, y, z) I x + 2y - z ≠ 0}.
We recognize that the set of all points in ℝ3 that are not in D form a plane in space that passes through the origin (with normal vector (1, 2, -1)).
We determine the range R is ℝ; that is, all real numbers are possible outputs of f. There is no set way of establishing this. Rather, to get numbers near 0 we can let y = 0 and choose z ≈ - x2. To get numbers of arbitrarily large magnitude, we can let z ≈ x + 2y.
Level Surfaces
If is very difficult to produce a meaningful graph of a function of three variables. A function of one variable is a curve drawn in 2 dimensions; a function of two variables is a surface drawn in 3 dimensions; a function of three variables is a hypersurface drawn in 4 dimensions.
There are a few techniques one can employ to try to “picture” a graph of three variables. One is an analogue to level curves: level surfaces. Given w = f(x, y, z), the level surface at w = c is the surface in space formed by all points (x, y, z) where f(x, y, z) = c.
Example: Finding level surfaces. If a point source S is radiating energy, the intensity I at a given point P in space is inversely proportional to the square of the distance between S and P. That is, when S = (0, 0, 0).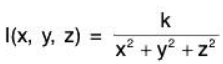 for some constant k.
for some constant k.
Let k = 1; find the level surfaces of I.
If energy (say, in the form of light) is emanating from the origin, its intensity will be the same at all points equidistant from the origin. That is, at any point on the surface of a sphere centered at the origin, the intensity should be the same. Therefore, the level surfaces are spheres.
We now find this mathematically. The level surface at I = c is defined byA small amount of algebra reveals
Given an intensity c, the level surface I = c is a sphere of radius 1/√c, centered at the origin.
Definition: Open Balls, Limit, Continuous
- An open ball in ℝ3 centered at (x0, y0, z0) with radius r is the set of all points (x, y, z) such that
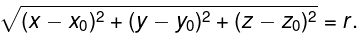
- Let D be an open set in ℝ3 containing (x0 , y0, z0), and let f(x, y, z) be a function of three variables defined on D, except possibly at (x0, y0, z0). The limit of f(x, y, z) as (x, y, z) approaches (x0, y0, z0) is L, denoted
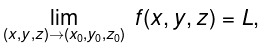 means that given any ε > 0, there is a δ > 0 such that for all (x, y, z)≠ (x0, y0, z0), if (x, y, z) is in the open ball centered at (x0, y0, z0) with radius δ, then lf(x, y, z) — L| < ε.
means that given any ε > 0, there is a δ > 0 such that for all (x, y, z)≠ (x0, y0, z0), if (x, y, z) is in the open ball centered at (x0, y0, z0) with radius δ, then lf(x, y, z) — L| < ε. - Let f(x, y, z) be defined on an open ball B containing (x0, y0, z0). f is continuous at (x0,y0,z0). if
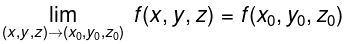
These definitions can also be extended naturally to apply to functions of four or more variables. Theorem also applies to function of three or more variables, allowing us to say that the function 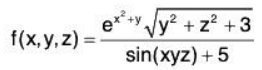 is continuous everywhere.
is continuous everywhere.
Partial Derivatives and Functions of Three Variables
The concepts underlying partial derivatives can be easily extend to more than two variables. We give some definitions and examples in the case of three variables and one can extend these definitions to more variables if needed.
Definition: Partial Derivatives with Three Variables. Let w = f(x, y, z) be a continuous function on an open set S in ℝ3.
The partial derivative of f with respect to x is :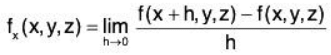 Similar definitions hold for fy(x, y, z) and fz(x, y, z).By taking partial derivatives of partial derivatives, we can find second partial derivatives of f with respect to z then y, for instance, just as before.
Similar definitions hold for fy(x, y, z) and fz(x, y, z).By taking partial derivatives of partial derivatives, we can find second partial derivatives of f with respect to z then y, for instance, just as before.
Example. Partial derivatives of functions of three variables.
For each of the following, find fx, fy, fz, fxz, fyz, and fzz.
- f(x, y, z) = x2y3r ’ + x2y2 + x3z3 + y4z4
- f(x, y, z) = x sin(yz)
1. fx = 2xy3z4 + 2xy2 + 3x2z3;
fy = 3x2y2z4 + 2x2y + 4y3z4;
fz = 4x2y3z3 + 3x3z2 + 4y4z3;
fxz = 8xy3z3 + 9x2z2;
fyz = 12x2y2z3 + 16y3z3;
fzz = 12x2y3z2 + 6x3z + 12y4z2
2. fx = sin(yz);
fy = xz cos(yz);
fz = xy cos(yz);
fxz = y cos(yz);
fyz = x cos(yz) - xyz sin(yz);
fzz = - xy2sin (xy)
Higher Order Partial Derivatives
We can continue taking partial derivatives of partial derivatives of partial derivatives of....; we do not have to stop with second partial derivatives.
We do not formally define each higher order derivative, but rather give just a few examples of the notation.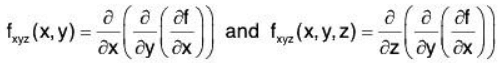
Example: Higher order partial derivatives.
1. Let f(x, y) = x2y2 + sin(xy). Find fxxy, and fyxx.
2. Let f(x, y, z) = x3exy + cos(z). Find fxyz.
- To find fxxy we first find fx, then fxx, then fxxy:
fx = 2xy2 + y cos(xy)
fxx = 2y2 - y2 sin<xy)
f = 4y - 2y sin(xy) - xy2 cos(xy).
To find fyxx we first find fy then fyx then fyxx :
fy = 2x2y + x cos(xy)
fyx= 4xy + cos(xy) - xy sin(xy)
fyxx= 4y - y sin(xy) - (y sin(xy) + xy2 cos(xy))
= 4y - 2y sin(xy) - xy2 cos(xy).
Note how = fxxy = fyxx.- To find f , we find fx, then fxy, then fxyz :
fx = 3x2exy + x3yexy
fxy = 3x3exy + x3 exy + x4yexy = 4x3exy + x4yexy
fxyz =0
In the previous example we saw that fxxy= fyxx ; this is not a coincidence. While we do not state this as a formal theorem, as long as each partial derivative is continuous, it does not matter the order in which the partial derivatives are taken. For instance, fxxy = fxyz = fyxx.
Differentiability of Functions of Three Variables
The definition of differentiability for functions of three variables is very similar to that of functions of two variables. We again start with the total differential.
Definition : Total Differential. Let w = f(x, y, z) be continuous on an open set S. Let dx, dy and dz represent changes in x, y and z, respectively. Where the partial derivatives fx, fy and fz exist, the total differential of w is
dz = fx(x, y, z)dx + fy(x, y, z)dy + fz(x, y, z)dz .
This differential can be a good approximation of the change in w when w = f(x, y, z) is differentiable.
Definition : Multivariable Differentiability. Let w = f(x, y, z) be defined on an open ball B containing (x0, y0, z0) where fx(x0, y0, z0), fy(x0, y0, z0) and fz(x0, y0, z0) exist. Let dw be the total differential of w at (x0, y0, z0). Let Δw = f(x0 + dx, y0 + dy, z0 + dz) - f(x0, y0, z0), and let Ex, Ey and Ez be functions of dx, dy and dz such that
Δw = dw = Exdx + Eydy + Ezdz
- f is differentiable at (x0, y0, z0) if, given ε > 0, there is a δ > 0 such that if ll<dx, dy, dz)ll < δ, then ll<Ex, Ey , Ez >ll < ε.
- f is differentiable on B if f is differentiable at every point in B. If f is differentiable on ℝ3, we say that f is differentiable everywhere.
Just as before, this definition gives a rigorous statement about what it means to be differentiable that is not very intuitive. We follow it with a theorem similar to Theorem.
Theorem: Continuity and Differentiability of Functions of Three Variables.
Let w = f(x, y, z) be defined on an open ball B containing (x0, y0, z0).
- If f is differentiable at (x0, y0, z0), then f is continuous at (x0, y0, z0).
- If fx, fy and fz are continuous on B, then f is differentiable on B.
This set of definition and theorem extends to functions of any number of variables. The theorem again gives us a simple way of verifying that most functions that we encounter are differentiable on their natural domains.
This section has given us a formal definition of what it means for a functions to be "differentiable," along with a theorem that gives a more accessible understanding. The following sections return to notions prompted by our study of partial derivatives that make use of the fact that most functions we encounter are differentiable.
Maxima & Minima of Three Variables Functions
Let u = f(x, y, z) be a function of three variables x, y and z, then we can find the maximum and minimum value of the function as like the two variables.
Suppose f(x, y, z) is a given function of three independent variables x, y and z.
- Find
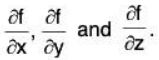
- Now solve the equations
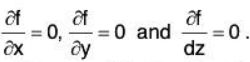
- After solving we get the points at which the function f(x, y, z) may be maximum or a minimum that are (a1, b1, c1), (a2, b2, c2), ...
- To discuss the maximum or minimum value of f(x, y, z) at any point (a1, b1, c1), find six partial derivative at this point.
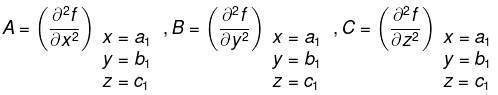
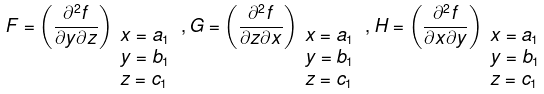
- Find the expression
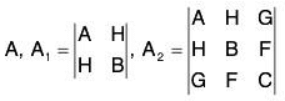 ..... (1)
..... (1) - If all A, A1, and A2 are positive, then f(x, y, z) is minimum at (a1, b1, c1).
- If A, A1, and A2 are alternately negative and positive, then f(x, y, z) is maximum at (a1, b1, C1)
- If above conditions not satisfied, then f(x, y, z) is neither maximum nor minimum at (a1, b1, c1).
Example: Discuss the maximum and minimum value of
u = x2 + y2 + z2 + x - 2z - xy.
As given
u = x2 + y2 + z2 + x - 2z - xy, then
ux = 2x - y + 1 = 0, uy = -x + 2y = 0, uz = 2z - 2 = 0.
On solving these equations we get x = -2/3, y = -1/3, z = 1. Therefore 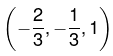 is only critical point where function will be either maximum or minimum. Now we will decide it.Now the values of following derivatives A = 2, B = 2, C = 2, F = 0, G = 0, H = -1
is only critical point where function will be either maximum or minimum. Now we will decide it.Now the values of following derivatives A = 2, B = 2, C = 2, F = 0, G = 0, H = -1
Now we have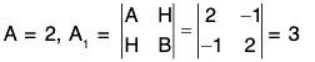
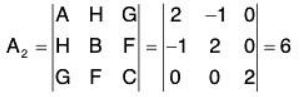
Since all these A, A1, and A2 are positive, we have a minimum of u at the point 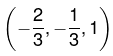
Example: Show that the point such that the sum of the sum of the squares of its distances from n given points shall be minimum, is the center of the mean position of the given points. Let the n given points be (a1, b1, c1), (a2, b2, c3), ... (an, bn, cn) and let (x, y, z) be the coordinate of the required point.
If u denotes the sum of the squares of the distances of (x, y, z) from the n given points, then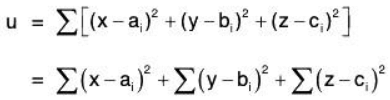
For maximum or a minimum of u, we must have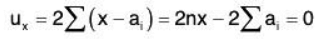 .....(2)
.....(2)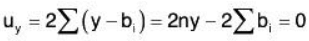 ...... (3)
...... (3)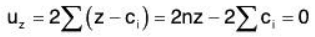 ...... (4)
...... (4)
Solving these above equations, we get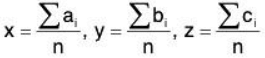
Now A = 2n, B = 2n, C = 2n, F = G = H = 0
We have A = 2n1, A1 = 4n2, A2 = 8n3. Since there three expression are all positive, u is minimum when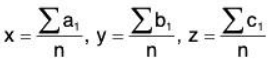
So u is minimum when the point (x, y, z) is the centre of the mean position of the n given points.
Example 1: Find the range of 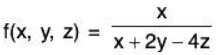
x + 2y - 4z ≠ 0; the set of points of ℝ3 NOT in the domain form a plane through the origin. Range: ℝ
Example 2: Find the range of 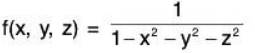
x2 + y2 + z2 ≠ 1; the set of points in ℝ3 NOT in the domain form a sphere of radius 1.
Range: (-∞, 0) U [1, ∞)
Example 3: Find the range of 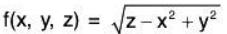
z ≥ x2 - y2; the set of points in ℝ3 above (and including) the hyperbolic paraboloid z = x2 - y2. Range: [0, ∞)
Method of Lagrange Multiplier
The method of Lagrange multipliers allows us to maximize or minimize functions with the con straint that we only consider points on a certain surface. To find critical points of a function f(x, y, z) on a level surface g(x, y, z) = C (or subject to the constraint g(x, y, z) = C), we must solve the following system of simultaneous equations:
∇f(x,y,z) = λ∇g(x,y,z)
g(x, y, z) = C
Remembering that ∇f and ∇g are vectors, we can write this as a collection of four equations in the four unknowns x, y, z, and λ:
fx(x,y, z) = λgx(x, y, z)
fy(x,y, z) = λgy(x, y, z)
fz(x,y, z) = λgz(x, y, z)
g(x, y, z) = C
The variable λ is a dummy variable called a “Lagrange multiplier”; we only really care about the values of x, y, and z.
Once you have found all the critical points, you plug them into f to see where the maxima and minima of the function occurs. The critical points where f is greatest are called points of maxima and the critical points where f is smallest are called points of minima.
Example 1: Use the method of Lagrange multipliers to maximize f(x, y) = 3xy.
subject to the constraint x + y = 8.
First let f(x, y) = 3xy and g(x, y) = x + y - 8.
then defined a new function F as
F(x, y, z) = f(x, y) - λg(x, y)
= 3xy - λ(x + y - 8)
To find the critical numbers of F, begin by finding the partial derivatives of F with respect to x, y and λ. Then, set of partial derivatives equal to zero.Fx(x, y, λ) = 3y - λ ⇒ 3y - λ = 0 ...(1)
Fy(x, y, λ) = 3x - λ ⇒ 3x - λ = 0 ...(2)
Fz(x, y, λ) = -x - y + 8 ⇒ -x-y + 8 = 0 ...(3)
Solving for λ in the first equation (1) gives
3y - λ = 0 ⇒ λ = 3y
Substituting for λ in the second (2) equation
3x - 3y = 0 ⇒ 3x - 3y or x = y
Now, substitute the value of x in equation (3).
- y - y + 8 = 0
2y = 8
y = 4
Using this value, we can conclude that the critical values are x = 4, y = 4. Which implies that the maximum is
f(x, y) = 3xy
= 3(4)(4) = 48.
Example 2: Find the maximum of V = xyz subject to the constraint 6x + 4y + 3z - 24 = 0
First, let f(x, y, z) = xyz and g(x, y, z) = 6x + 4y + 3z - 24.
Then, define a new function F as F(x, y, z, λ) = f(x, y, z) - λg(x, y, z)
= xyz - X(6x + 4y + 3z - 24).To find the critical numbers of F, begin by finding the partial derivatives of F with respect to x, y, z, and λ. Then, set the partial derivatives equal to zero.
Fx(x, y, z, λ ) = yz - 6λ ⇒ yz - 6λ = 0
Fy(x, y, z, λ) = xz - 4λ ⇒ xz - 4λ = 0
Fz(x, y, z, λ) = xy - 3λ ⇒ xy - 3λ = 0
F. (x, y, z, λ) = - 6x - 4y - 3z + 24 ⇒ -6x - 4y - 3z + 24 = 0
Solving for λ in the first equation producesSubstituting for λ in the second and third equations produces the following.
Next, substituting for y and z in the equation Fx(x, y, z, λ) = 0 and solve for x.
Using this x-value, you can conclude that the critical values are x = 4/3, y = 2 and z = 8/3. which implies that the maximum is V = xyz. Write objective function
Example 3: Minimize: f(x, y) = x2 + y2
Subject to : 2x + 6y = 2000
f(x, y) = x2 + y2
g(x, y) = 2x + 6y - 2000 = 0.L(x, y, λ) = x2 + y2 - λ (2x + 6y - 2000)
Lx(x, y, λ) = 2x - 2λ ⇒ 2x - 2λ = 0 ...(1)
Ly(x , y, λ) = 2y - 6λ ⇒ 2y - 6λ = 0 ...(2)
Lλ(x, y, λ) = - 2 x - 6y + 2000 ⇒ - 2 x - 6y + 2000 = 0 ...(3)Solving for X
2x — 2λ = 0 => λ = x
Putting value of λ in (2).
2y + 6x = 0 => 6x = 2y, y = 3xNow Substituting y in (3)
-2x - 18x + 2000 = 0
⇒ -20x + 2000 = 0
x = 100
Using the value of x we can conclude that the critical points are x = 100, y = 300.
Therefore the min value in f(100, 300) = (100)2 + (300)2= 10000 + 90000 = 1,00,000
Example 4: Find the maximum and minimum values of f(x, y) = 81x2 + y2 subject to the constraint 4x2 + y2 = 9.
Let f(x, y) = 81 x2 + y2
g(x, y) = 4x2 + y2 - 9
Then define a new function F as
F = f(x, y) - λg(x, y)
= 81 x2 + y2 - λ(4x2 + y2 - 9)
Fx(x, y, λ) = 162x - 8λx
⇒ 162x - 8λx ..... (1)
Fy(x, y, λ) = 2y - 2yλ
⇒ 2y - 2yλ = 0 ...(2)
Fλ (x, y, λ) = - 4x2 - y2 + 9
⇒ -4x2- y2 + 9 = 0 ...(3)
Solve for λ Let’s start with the second one.
2y = 2yλ
⇒ λ = 1 or y = 0
Let y = 0, then in this caseTherefore we get two points that are absolute extrema
Now Let λ = 1, in this case equation (1) reduces to162x = 8x ⇒ 154x = 0 ⇒ x = 0
under this assumption we must have x = 0. Now substitute in (3) we get
y2 = 9 ⇒ y = ± 3
So this gives us two more points that are absolute extreme
(0, -3) and (0, 3)
Now, we have four points that are absolute extrema to determine the absolute extrema we need to evaluate the function at each of these pointsThe absolute maximum is 729/4 = 182.25 which occurs at
The absolute minimum is which occurs at (0, -3) and (0, 3).
Example 5 : Find the maximum values of f(x, y) = 8x2- 2y subject to the constraint x2+ y2=1.
Given f(x, y) = 8x2 - 2y
g(x, y) = x2 + y2 - 1
F(x, y, λ) = f(x, y) - λg(x, y) = 8x2 - 2y - λ(x2 + y2- I)
Fx = 16x - 2λx ⇒ 16x - 2λx = 0 ...(1)
Fy = -2 - 2λy ⇒ -2 - 2λy = 0 ...(2)
F = - x2 - y2 + 1 ⇒ - x2 - y2 + 1 = 0
Solve for λ
by (1) 16x - 2λx = 0
⇒ x = 0 or λ = 8
Let x = 0 then by (3), we get
y2 = 1 ⇒ y = ±1
Therefore, we get two points that are absolute extrema (0, -1) and (0, 1) Now assume λ = 8. In this case, we can plug the value in equation (2) we get.
-2 = 16y ⇒ y = -1/8
we now plug the value of y in equation (3)this gives two more points that are absolute extrema.
Now
f(0, - 1 ) = 2, f(0,1) = - 2
The absolute maximum is 65/8 = 8.125 occurs at
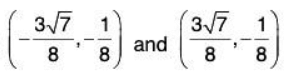
Example 6: Find the minimum values of f(x, y, z) = xyz subject to the constraint x + 9y2 + z2 = 4. Assume that x > 0.
f(x, y, z) = xyz
g(x, y, z) = x + 9y2 + z2 = 4, x ≥ 0
F(x, y, z, λ) = f(x, y, z) - λg(x, y, z)
= xyz - λ(x + 9y2 + z2 - 4)
Fx = yz - λ ⇒ yz - λ = 0 ...(1)
Fy = xz - 18λy ⇒ xz - 18λy = 0 ...(2)
Fz = xy - 2λz ⇒ xy - 2λz = 0 ...(3)
Fλ = -x - 9y2 - z2 + 4 ⇒ x2 + 9y2 + z2 - 4 = 0 ...(4)
Now multiplying equation (1) by x, equation (2) by y and equation (3) by z.
We getxyz = λx ...(5)
xyz = 18λy2 ...(6)
xyz = 2λz2 ...(7)
by equation (5) and (6)
xλ = 18λy2 (x - 18y2)λ = 0
⇒ x = 18y2 or λ = 0
by equation (6) and (7)18y2λ = 2z2λ ⇒ (18y2 - 2z2)λ = 0
⇒ z2 = 9y2 or λ = 0
Now we have two possibilities Either λ = 0 or we have x = 18y2 and z2 = 9y2.
Let λ = 0, then by equation (1), (2) and (3) we haveyz = 0 ⇒ y = 0 or z = 0 ...(8)
xz = 0 ⇒ x = 0 or z = 0 ...(9)
xy = 0 ⇒ x = 0 or y = 0 ...(10)
from this we noticed that we can’t have all three of the variables be zero but we could have two of then be zero. So this leads to the following two cases that we can plug into the constraint t find the value of the third variable.
y = 0, x = 0 ⇒ z2 = 4 => z = ±2
y = 0,z = 0:x = 4
So this gives us the following three absolute extrema
(0, 0, -2), (0, 0, 2) and (4, 0, 0)
Now, let’s check the second possibility from equation (8) z = 0. In this case the (9) equation while be 0 = 0 and so will not be any use. Then (10) however, has the possibilities of x = 0 or y = 0.
z = 0, x = 0 : 9y2 = 4 ⇒ y = ± 2/3
This leads to two more absolute extremawe had another possibility x = 18y2 and z2 = 9y2
In this case we can plug each of these directly into the constraint to get the following
18y2 + 9 y2 + 9y2 = 36y2 = 4 ⇒ y = ± 1/3
NowTherefore we get the following four absolute extrema
Now
The absolute minimum is -2/3 which occurs at
|
98 videos|34 docs|32 tests
|
FAQs on Functions of Two or Three Variables- II - Mathematics for Competitive Exams
| 1. What are the maxima and minima of functions of two variables? |  |
| 2. How can we find the maxima and minima of functions of three variables? |  |
| 3. What is the method of Lagrange multipliers? |  |
| 4. How do functions of two or three variables relate to the IIT JAM exam? |  |
| 5. What are some frequently asked questions about functions of two or three variables in the IIT JAM exam? |  |