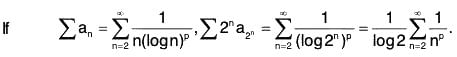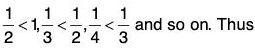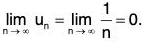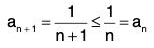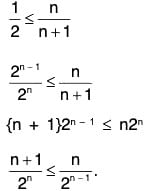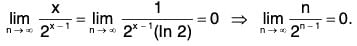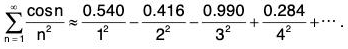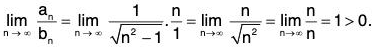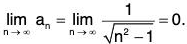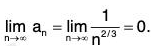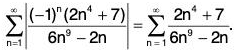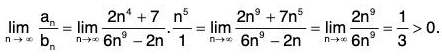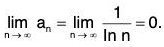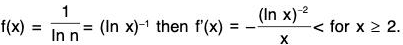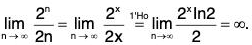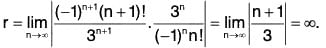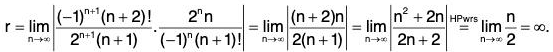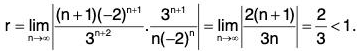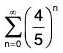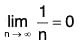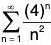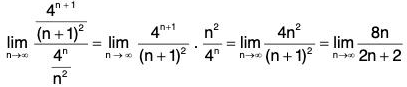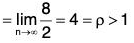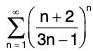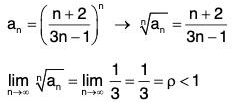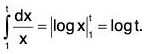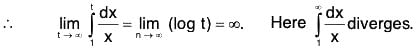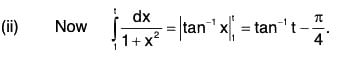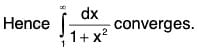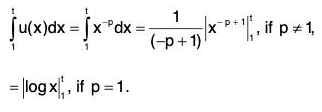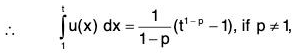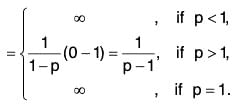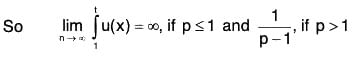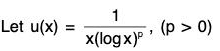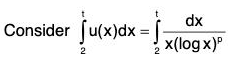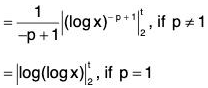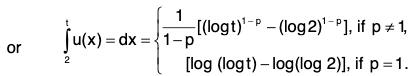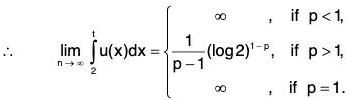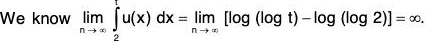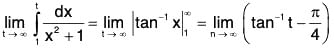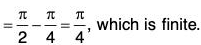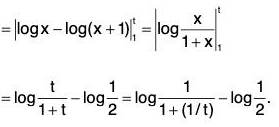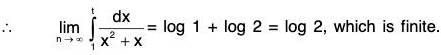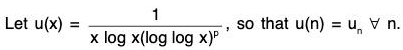Series of Real Numbers- II | Mathematics for Competitive Exams PDF Download
| Table of contents |

|
| Cauchy’s Condensation Test |

|
| Alternating Series |

|
| Absolute and Conditional Convergence |

|
| Convergence of the Infinite Integral |

|
Cauchy’s Condensation Test
Statement: For a non-increasing sequence {an} of non-negative real numbers, the series ∑an converges if and only if the series
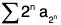 converges.
converges.Proof: Observe that since {an} is decreasing:
a1 + (a2 + a3) + (a4 + a5 + a6 + a7) +...+ aN ≤ a1 + 2a2 + 4a4 + ... +
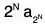
⇒
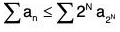
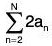 = a2 + (a2 + a3) + (a3 + 2a4 + a5) + (a5 + 2a6 + 2a7 + 2a8 + a9) +... + 2aN ≥ a2 + 2a4 + 4a8 + 8a16 + .....+
= a2 + (a2 + a3) + (a3 + 2a4 + a5) + (a5 + 2a6 + 2a7 + 2a8 + a9) +... + 2aN ≥ a2 + 2a4 + 4a8 + 8a16 + .....+ 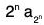
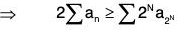
Thus proved.
Example 1: Discuss convergence of 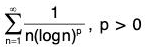
is monotone decreasing as log n is increasing.
Thus, the series converges iff p > 1.
Statements of two important tests for series with arbitrary terms :
Abel's test : If {(xn)} is a convergent monotone sequence and the series ∑yn is convergent, then the series ∑xnyn is also convergent.
Dirichlet's test: If {(xn)} is a decreasing sequence with lim xn = 0, and if the partial sums {(sn)} of ∑yn are bounded, then the series ∑xnyn is convergent.
Alternating Series
A series of the form u1 - u2 + u3 - u4 + ..., where un > 0 ∀ n ∈ N is called an alternating series and is denoted by
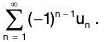
We have
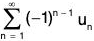 = u1 - u2 + u3 - u4 + ... + (-1)n-1 un + ...
= u1 - u2 + u3 - u4 + ... + (-1)n-1 un + ...Example: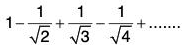
Leibnitz Test
If an alternating series 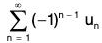 satisfies
satisfies
(i) Each term is numerically less than the proceeding term i.e.
un ≤ un-1 ∀ n,
(ii) 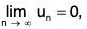
then the series ∑(-1)n-1 un converges.
Proof : In order to prove that the given series converges, we shall show that its sequence 〈Sn〉 of partial sums converges. For this we shall first prove that the subsequences 〈Sn〉 and 〈S2n + 1〉 both converge to the same limit.
Now = S2n = u1 - u2 + u3 - u4 + .... + u2n - 1 - u2n,
and S2n+2 = u1 - u2 + u3 - u4 + .... + u2n-1 - u2n + u2n+1 - u2n +2.
∴ S2n+2 - S2n + u2n + 1 - u2n + 2 ≥ 0. (∵ Un+1 ≤ un < ∀ n )
Thus 〈S2n〉 is a monotonically increasing sequence.
Again S2n = u1 - u2 + u3 - u4 + u5 - u6 + ... + u2n-1, - u2n
= u1 - [(u2 - u3) + (u4 - u5) + ... + (U2n-2 - u2n-2) + u2n]
Now each term within the bracket is positive, since
un+1 ≤ un ∀ n and u2n > 0.
∴ S2n < u1 ∀ n and so 〈S2n〉 is bounded above.
Since 〈S2n〉 is monotonically increasing and bounded above, therefore 〈S2n〉 is convergent.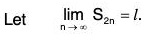 ....(iii)
....(iii)
We shall now show that 〈S2n + 1〉 converges to l. We have
S2n + 1 = u1 - u2 + u3 - u4 + .... + u2n - 1 , - u2n + u2n + 1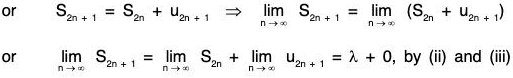
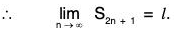
From (iii), (iv), it follows that for any ε > 0, there exists positive integers m1 and m2 such that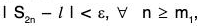 ...(v)
...(v)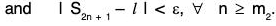 ....(vi)
....(vi)
Let m = max (m1, m2) so that m ≥ m1, m ≥ m2, .....(vii)
From (v), (vi), (vii) ;
⇒ 〈Sn〉 converges to l.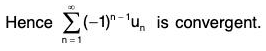
Remark: The alternating series ∑(-1)n-1 un will not be convergent if either 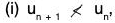
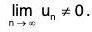
For Example 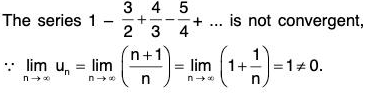
Example:
This is an alternating series
So we can check the convergence by applying leibnitz test
and so on
i.e. Each term of an is decreasing
So by Leibnitz test the given series converges.
Example 1: Test for convergence the series
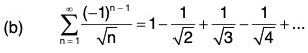
We have
(i) un+1 < un ∀ n,
(ii)
Hence, by Leibnitz’s Test, the given series is convergent.
(b) The proof of similar. The given series is convergent.
Example 2: Using the Alternating Series Test
Determine the convergence or divergence of 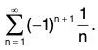
Note that
So, the first condition of Theorem is satisfied. Also note that the second condition of Theorem satisfied because
for all n. So, applying the Alternating Series Test, you can conclude the series converges.
Example 3: Using the Alternating Series Test
Determine the convergence or divergence of 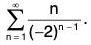
To apply the Alternating Series Test, note that, for n ≥ 1,
So, an+1 = (n + 1)/2n ≤ n/2n - 1 = an for all n. Furthermore, by L’Hopital's Rule,
Therefore, by the Alternating Series Test, the series converges.
Example: When the Alternating Series Test Does Not Apply
a. The alternating series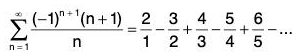
passes the second condition of the Alternating Series Test because an + 1 ≤ an for all n. You cannot apply the Alternating. Series Test, however, because the series does not pass the first condition. In fact, the series diverges.
b. The alternating series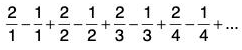
passes the first condition because an approaches 0 as n → ∞. You cannot apply the Alternating Series Test, however, because the series does not pass the second condition. To conclude that the series diverges, you can argue that S2N equals the Nth partial sum of the divergent harmonic series. This implies that the sequence of partial sums diverges. So, the series diverges.
Example: The alternating harmonic series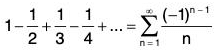
satisfies
(i) bn+1 < bn because 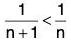
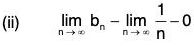
So the series is convergent by the Alternating Series Test.
Absolute and Conditional Convergence
Sometimes series have both positive and negative terms but they are not perfectly alternating like those in the previous section. For example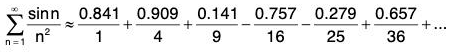
is not alternating but does have both positive and negative terms.
So how do we deal with such series? The answer is to take the absolute value of the terms. This turns the sequence into a non-negative series and now we can apply many of our previous convergence tests. For example if we take the absolute value of the terms in the series above, we get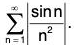
Since Isin nl ≤ 1, then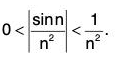
But 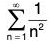 converges by the p-series test (p = 2 > 1), so
converges by the p-series test (p = 2 > 1), so 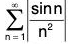 converges by comparison.
converges by comparison.
But what about the original series 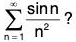 The next theorem provides the answer: The series does converge.
The next theorem provides the answer: The series does converge.
Theorem: (The Absolute Convergence Test). If 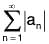 converges so does
converges so does 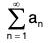
Proof. Given 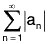 converges. Define a new series
converges. Define a new series 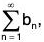 where
where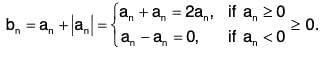
So 0 ≤ bn = an + lanl < lanl + lanl = 2lanl. But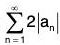 converges, hence by direct comparison
converges, hence by direct comparison 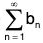 converges. Therefore
converges. Therefore

converges since it is the difference of two convergent series.
Important Note: The converse is not true. If  converges,
converges,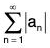 may or may not converge.
may or may not converge.
For example, the alternating harmonic series 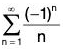 converges, but if we take the absolute value of the terms, the harmonic series
converges, but if we take the absolute value of the terms, the harmonic series 
This leads to the following definition.
Absolute Convergence
A series ∑un is said to be absolutely convergent if the series ∑ I un I is convergent.
Example: The series 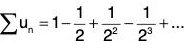 is absolutely convergent, since
is absolutely convergent, since 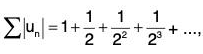 being a geometric series with common ratio r = 1/2 < 1, is convergent.
being a geometric series with common ratio r = 1/2 < 1, is convergent.
Example 1: Determine whether 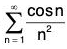 converges absolutely, conditionally, or not at all.
converges absolutely, conditionally, or not at all.
Notice that this series is not positive nor is it alternating since the first few terms are approximately
First we check absolute convergence.looks a lot like the p-series
with P = 2 > 1. We can use the direct comparison test. Since 0 ≤ Icos nl ≤ 1,
for all n. Since the p-series
converges, so does
by the direct comparison test (Theorem). So the series of absolute values converges. The original series is absolutely convergent. We need to check further.
Conditional Convergence
A series ∑un is said to be conditionally convergent, if
(i) ∑un is convergent and
(ii) ∑un is not absolutely convergent.
Example: The series 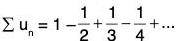 is conditionally convergent, since the given series is convergent (by Leibnitz Test) and
is conditionally convergent, since the given series is convergent (by Leibnitz Test) and 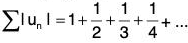 is not convergent, i.e., ∑un is not absolutely convergent.
is not convergent, i.e., ∑un is not absolutely convergent.
Example 1: Determine whether 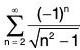 converges absolutely, conditionally, or not at all.
converges absolutely, conditionally, or not at all.
First we check absolute convergence.
Notice thatSo let’s use the limit comparison test. The terms of the series are positive and
Since the harmonic seriesdiverges (p-series with p = 1), then
diverges by the limit comparison test. So the series does not converge absolutely.
Since the series is alternating and not absolutely convergent, we check for conditional convergence using the alternating series test withCheck the two conditions.
- Further an+1 ≤ an is decreasing because
(You could also show the derivative is negative.) Since the two conditions of the alternating series test are satisfied,
is conditionally convergent by the alternating series test.
Example: Determine whether  is aK p-series with
is aK p-series with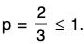
So the series of absolute values diverges. The original series is not absolutely convergent.
Since the series is alternating and not absolutely convergent, we check for conditional convergence using the alternating series test with 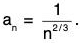 Check the two conditions.
Check the two conditions.
Since the two conditions of the alternating series test are satisfied, 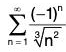 is conditionally convergent by the alternating series test..
is conditionally convergent by the alternating series test..
Theorem: Every absolutely convergent series is convergent. The converse need not be true.
Proof: Let ∑un be an absolutely convergent series.
Then ∑ I un I is convergent.
By cauchy’s General Principle of Convergence, for any ε > 0, there exists a positive integer m s.t.
I I um + 1 I + I um + 2 I + ... + I un I I < ε, ∀ n ≥ m
⇒ I um + 1 I + I um + 2 I + ... + I un I < ε, ∀ n ≥ m.
Now I um + 1 + um + 2 + ... + un I ≤ I um + 1 I + I um + 2 I + ... + I un I < ε ∀ n ≥ m.
Hence ∑ un is convergent (by Cauchy’s Principle of Convergence).
(ii) The converse of the theorem is not true i.e.,
A convergent series may not be absolutely convergent.
Consider the series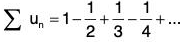
We have seen that the given series is convergent, by Leibnitz’s Test but 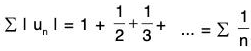 s not convergent i.e. ∑ un is not absolutely convergent.
s not convergent i.e. ∑ un is not absolutely convergent.
Example 1: Determine whether 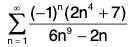 converges absolutely, conditionally, or not at all.
converges absolutely, conditionally, or not at all.
First we check absolute convergence.
Notice thatSo let’s use the limit comparison test. The terms of the series are postive and
Sinceconverges (p-series with p = 5 > 1), then
converges by the limit comparison test. So the series converges absolutely.
Example 2: Determine whether 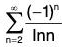 converges absolutely, conditionally, or not at all.
converges absolutely, conditionally, or not at all.
First we check absolute convergence.
We use the direct comparison test with
Notice that
because n > 1. Next
(To check that
diverges, use the integral test and u = substitution with u = In x.
In lln bl - ln(ln 2) = +∞. Consequently
diverges by the direct comparison test. So the series does not converges absolutely.
Since the series is alternating and not absolutely convergent, we check for conditional convergence using the alternating series test withCheck the two conditions.
- Further an is decreasing since
Since the two conditions of the alternating series test are satisfied,
is conditionally convergent by the alternating series test.
Example 3: Determine whether 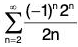 converges absolutely, conditionally, or not at all.
converges absolutely, conditionally, or not at all.
First we check absolute convergence.
Use the nth term test:
Since limn→∞ an ≠ 0 the series automatically diverges and cannot converge absolutely or conditionally.
When we test for absolute convergence using the ratio test, we can say more. If the ratio r is actually greater than 1, the series will diverge. We don’t even need to check conditional convergence.
Theorem (The Ratio Test Extension):
Assume that  is a series with non-zero terms and let
is a series with non-zero terms and let 
- If r < 1, then the series
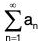 converges absolutely.
converges absolutely. - If r > 1 (including ∞) , then the series
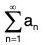 diverges.
diverges. - If r = 1, then the test is inconclusive. The series may converge or diverge.
This is most helpful when the series diverges. It says we can check for absolute convergence and if we find the absolute value series diverges, then the original series diverges. We don’t have to check for conditional convergence.
Example 1: Determine whether  conver ges absolutely, conditionally, or not at all.
conver ges absolutely, conditionally, or not at all.
Here’s a perfect place to use the ratio test because there is a factorial.
The (original) series diverges by the ratio test. The ratio test says we don’t have to check for conditional convergence.
Example 2: Determine whether 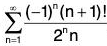 converges absolutely, conditionally, or not at all.
converges absolutely, conditionally, or not at all.
First we check absolute convergence using the ratio test because of the factorial.
The (original) series diverges by the ratio test extension.
Example 3: Determine whether 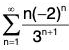 converges absolutely, conditionally, or not at all.
converges absolutely, conditionally, or not at all.
Check absolute convergence using the ratio test extension.
The (original) series converges absolutely by the ratio test extension.
Example 4: Does the following series converge absolutely, converge conditionally, or diverge?
Let us look at the positive term series for this given series.
This is a geometric series with ratio, r = 4/5, which is less than 1.
Therefore this series converges, and the given series converges absolutely.
Example 5: Does the following series converge absolutely, converge conditionally, or diverge?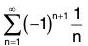
Let us look at the positive term series for the given series.
This is the harmonic series and it diverges, so the given series will not converge absolutely. Now we must determine if the given series will converge conditionally or diverge. To do this, we will have to look at the alternating series. To do this, we must use the alternating series test.
Let un = 1/n.
un > 0 for all n ≥ 1, so the first condition of this test is satisfied.
Now we must determine if the second condition is satisfied. This is easy to see. As n gets larger, the fraction 1/n gets smaller. So un ≥ un+1 and the second condition is true. Now let us determine if the third condition is satisfied.
The third condition holds, so the alternating series converges, and the given series converges conditionally.
So here the steps you will need to follow when determining absolute convergence, conditional convergence or divergence of a series. Look at the positive term series first. If the positive term
A. If it converges, then the given series converges absolutely.
B. If the positive terms series diverges, use the alternating series test to determine if the alternating series converges. If this alternating series diverges, then the given series diverges.
Example 6: Does the following series converge absolutely, converges conditionally, or diverges?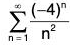
Here is the positive term series.
we are going to use the ratio test to determine the convergence of this series.
So the positive term series diverges by the ratio test, and the given series does not converge absolutely. Therefore, we will have to look at the alternating series to determine if it converges or not.
un is positive for n ≥ 1, so the first condition is satisfied. Now to determine it the second condition is holds. To help me determine this, we will plot the first 5 term of this sequence.Therefore, the third condition is not satisfied because the terms of this sequence are increasing. In fact 4n grows faster than n2. So the alternating series diverges, and the given series also diverges.
Example 7: Does the following series converge absolutely, converge conditionally, or diverge?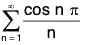
Since the cos nπ is the alternating term, the positive term series is the harmonic series. Remember that the harmonic series diverges, so the given series does not converge absolutely. Now to determine the convergence of the alternating series.
Let un = 1/n.
un > 0 for all n ≥ 1, so the first condition of this test satisfied.
Now we must determine if the second condition is satisfied. This is easy to see. As n gets larger, the fraction 1/n gets smaller. So un ≥ un + 1 and the second condition is true. Now let us determine if the third condition is satisfied.
The third condition holds, so the alternating series converges, and the given series converges conditionally.
Example 8: Does the following series converge absolutely, converge conditionally, or diverge?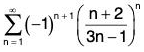
Here is the positive term series.
Since nth term is raised to the nth power, we will use the nth-root test to determine convergence or divergence of this series.
The positive term series converges by the nth-root test. Therefore, the given series converges absolutely.
Convergence of the Infinite Integral
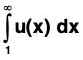
Definition: The infinite integral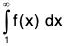 is said to be convergent (divergent), if
is said to be convergent (divergent), if 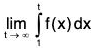 is finite (infinite).
is finite (infinite).
We state a result without proof:
Theorem: If f(x) ≥ 0 ∀ x ≥ 1, then 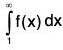 is convergent iff there exists a positive number k such that for
is convergent iff there exists a positive number k such that for 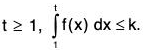
Example 1: Examine the convergence and divergence of
(i) 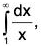
(ii) 
(i) We have
Definition: Let f(x) be a real valued function with domain [1, ∞[.
The function f(x) is said to be non-negative, if f(x) ≥ 0 ∀ x ≥ 1.
The function f(x) is said to be monotonically decreasing, if x ≤ y ⇒ f(x) ≥ f(y) ; x, y ∈ [1, ∞[.
For example, f(x) = 1/x2 is non-negative and monotonically decreasing ∀ x ≥ 1.
Cauchy’s Integral Test
If u(x) is a non-negative, monotonically decreasing and integrable function such that u(n) = un ∀ n ∈ N, then the series 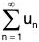 is convergent if and only if
is convergent if and only if 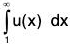 is convergent.
is convergent.
Proof : Since u(x) is monotonically decreasing, so
u(n) ≥ u(x) ≥ u(n + 1), when n ≤ x ≤ n + 1.
Since u(x) is non-negative and integrable, so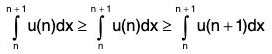
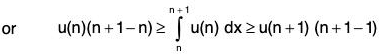
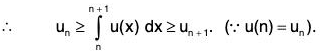 ....(1)
....(1)
Putting n = 1, 2, n - 1 in (1) and adding, we get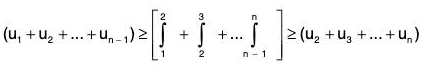
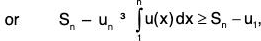 where Sn = u1 + u2 + ... + un-1 + un
where Sn = u1 + u2 + ... + un-1 + un 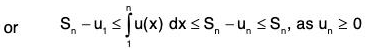 ....(2)
....(2)
The condition is necessary.
Suppose the series 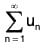 is convergent.
is convergent.
Then there exists a positive number K such that
Sn ≤ K ∀ n. ......(3)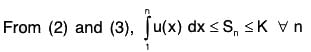
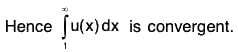
The condition is sufficient.
Then there exists a positive number k such that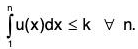 ....(4)
....(4)
From (2) and (4),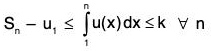
or Sn ≤ k + u1 ∀ n, so that 〈Sn〉 is bounded above.
Hence the series ∑ un is convergent.
Example 1: Show that the series 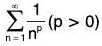 is convergent if p > 1 and divergent if p ≤ 1.
is convergent if p > 1 and divergent if p ≤ 1.
Let un = 1/np and u(x) = 1/xp , so that u(n) = un ∀ n ∈ N.
Clearly, for x ≥ 1, u(x) is non-negative, integrable and a decreasing function of x. Now
= (log t - log 1), if p = 1.(∵ log 1 = 0)
If Follows that the improper integralis convergent if p > 1 and divergent if p ≤ 1. Hence, by Cauchy’s integral test,
is convergent if p > 1 and divergent if p ≤ 1.
Example 2: Show that the series 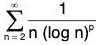 is convergent if p > 1 and divergent if 0 < p ≤ 1.
is convergent if p > 1 and divergent if 0 < p ≤ 1.
Then for x ≥ 2, u(x) is non-negative, monotonically decreasing and integrable function. Also u(n) = un ∀ n ∈ N.
Thusis convergent if p > 1 and divergent if 0 < p ≤ 1. Hence, by Cauchy’s Integral Test, the given series is convergent if p > 1 and divergent if 0 < p ≤ 1.
Example 3: Test for convergence the series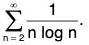
consider the case p = 1.
Hence the given series diverges.
Example 4: Apply Cauchy’s Integral Test to examine the convergence of the following series:
(i) 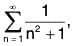
(ii)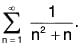
(i)
so that u(n) = un ∀ n ∈ N.
For x ≥ 1, u(x) is non-negative, monotonically decreasing and integrable function. Now
Thusis convergent and so
is convergent.
(By Cauchy’s Integral Test)
(ii)so that u(n) = un ∀ n ∈ N.
For x ≥ 1, u(x) is non-negative, monotonically decreasing and integrable function. Now
Thusdx is a convergent and so by Cauchy’s Integral Test, the given series is convergent.
Example 5: Test the convergent of
For x ≥ 3, u(x) is non-negative , monotonically decreasing and integrable function. Now
where y = log log x,
y1 = log log 3, y2 = log log t
Thusis convergent if p > 1 and divergent if 0 < p ≤ 1.
Hence, by Cauchy’s Integral Test, the given series is convergent if p > 1 and divergent if 0 < p ≤ 1.
|
98 videos|34 docs|32 tests
|
FAQs on Series of Real Numbers- II - Mathematics for Competitive Exams
| 1. What is Cauchy's Condensation Test and how is it used to determine the convergence of a series? |  |
| 2. What is an alternating series and how can we test its convergence? |  |
| 3. What is the difference between absolute and conditional convergence of a series? |  |
| 4. How can we determine the convergence of an infinite integral series? |  |
| 5. What are some important properties of the series of real numbers? |  |