Rotational Spectroscopy | Physical Chemistry PDF Download
Introduction
Rotational spectroscopy is concerned with the measurement of the energies of transitions between quantized rotational states of molecules in the gas phase. The spectra of polar molecules can be measured in absorption or emission by microwave spectroscopy or by far infrared spectroscopy.
Classification of molecular rotors
In quantum mechanics the free rotation of a molecule is quantized, so that the rotational energy and the angular momentum can take only certain fixed values, which are related simply to the moment of inertia, I, of the molecule. For any molecule, there are three moments of inertia: IA, IB and IC about three mutually orthogonal axes A, B, and C with the origin at the center of mass of the system. The general convention, used in this article, is to define the axes such that IA ≤ IB ≤ IC with axis A corresponding to the smallest moment of inertia. Some authors, however, define the A axis as the molecular rotation axis of highest order.
The particular pattern of energy levels (and, hence, of transitions in the rotational spectrum) for a molecule is determined by its symmetry. A convenient way to look at the molecules is to divide them into four different classes, based on the symmetry of their structure. These are:
Spherical tops (spherical rotors)
All three moments of inertia are equal to each other: IA = IB = IC. Examples of spherical tops include phosphorus tetramer (P4), carbon tetrachloride (CCl4) and other tetrahalides, methane (CH4), silane, (SiH4), sulfur hexafluoride (SF6) and other hexahalides. The molecules all belong to the cubic point groups Td or Oh.
Linear molecules
For a linear molecule the moments of inertia are related by IA ≪ IB= IC. For most purposes, IA can be taken to be zero. Examples of linear molecules include dioxygen, O2, dinitrogen, N2, carbon monoxide, CO, hydroxy radical, OH, carbon dioxide, CO2, hydrogen cyanide, HCN, carbonyl sulfide, OCS, acetylene (ethyne, HC≡CH) and dihaloethynes. These molecules belong to the point groups C∞v or D∞h.
Symmetric tops (symmetric rotors)
A symmetric top is a molecule in which two moments of inertia are the same, IA = IB or IB = IC. By definition a symmetric top must have a 3-fold or higher order rotation axis. As a matter of convenience, spectroscopists divide molecules into two classes of symmetric tops, Oblate symmetric tops (saucer or disc shaped) with IA = IB < IC and Prolate symmetric tops (rugby football, or cigar shaped) with IA < IB = IC. The spectra look rather different, and are instantly recognizable. Examples of symmetric tops include
- Oblate: Benzene, C6H6; ammonia, NH3; xenon tetrafluoride, XeF4
- Prolate: Chloromethane, CH3Cl, propyne, CH3C≡CH
As a detailed example, ammonia has a moment of inertia IC = 4.4128 × 10−47 kg m2 about the 3-fold rotation axis, and moments IA = IB = 2.8059 × 10−47 kg m2 about any axis perpendicular to the C3 axis. Since the unique moment of inertia is larger than the other two, the molecule is an oblate symmetric top.
Asymmetric tops (asymmetric rotors)
The three moments of inertia have different values. Examples of small molecules that are asymmetric tops include water, H2O and nitrogen dioxide, NO2 whose symmetry axis of highest order is a 2-fold rotation axis. Most large molecules are asymmetric tops.
Microwave and far-infrared spectra
Transitions between rotational states can be observed in molecules with a permanent electric dipole moment. A consequence of this rule is that no microwave spectrum can be observed for centrosymmetric linear molecules such as N2 (dinitrogen) or HCCH (ethyne), which are non-polar. Tetrahedral molecules such as CH4 (methane), which have both a zero dipole moment and isotropic polarizability, would not have a pure rotation spectrum but for the effect of centrifugal distortion; when the molecule rotates about a 3-fold symmetry axis a small dipole moment is created, allowing a weak rotation spectrum to be observed by microwave spectroscopy.
With symmetric tops, the selection rule for electric-dipole-allowed pure rotation transitions is ΔK = 0, ΔJ = ±1. Since these transitions are due to absorption (or emission) of a single photon with a spin of one, conservation of angular momentum implies that the molecular angular momentum can change by at most one unit. Moreover, the quantum number K is limited to have values between and including +J to -J.
Raman spectra
For Raman spectra the molecules undergo transitions in which an incident photon is absorbed and another scattered photon is emitted. The general selection rule for such a transition to be allowed is that the molecular polarizability must be anisotropic, which means that it is not the same in all directions. Polarizability is a 3-dimensional tensor that can be represented as an ellipsoid. The polarizability ellipsoid of spherical top molecules is in fact spherical so those molecules show no rotational Raman spectrum. For all other molecules both Stokes and anti-Stokes lines can be observed and they have similar intensities due to the fact that many rotational states are thermally populated. The selection rule for linear molecules is ΔJ = 0, ±2. The reason for the values ±2 is that the polarizability returns to the same value twice during a rotation. The value ΔJ = 0 does not correspond to a molecular transition but rather to Rayleigh scattering in which the incident photon merely changes direction.
The selection rule for symmetric top molecules is
ΔK = 0
If K = 0, then ΔJ = ±2
If K ≠ 0, then ΔJ = 0, ±1, ±2
Transitions with ΔJ = +1 are said to belong to the R series, whereas transitions with ΔJ = +2 belong to an S series. Since Raman transitions involve two photons, it is possible for the molecular angular momentum to change by two units.
Units
The units used for rotational constants depend on the type of measurement. With infrared spectra in the wavenumber scale  , the unit is usually the inverse centimeter, written as cm−1, which is literally the number of waves in one centimeter, or the reciprocal of the wavelength in centimeters
, the unit is usually the inverse centimeter, written as cm−1, which is literally the number of waves in one centimeter, or the reciprocal of the wavelength in centimeters 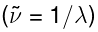 . On the other hand, for microwave spectra in the frequency scale
. On the other hand, for microwave spectra in the frequency scale 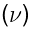 , the unit is usually the gigahertz. The relationship between these two units is derived from the expression
, the unit is usually the gigahertz. The relationship between these two units is derived from the expression
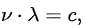
where ν is a frequency, λ is a wavelength and c is the velocity of light. It follows that
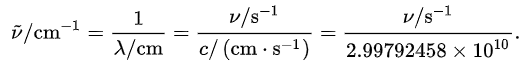
As 1 GHz = 109 Hz, the numerical conversion can be expressed as
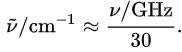
The population of vibrationally excited states follows a Boltzmann distribution, so low-frequency vibrational states are appreciably populated even at room temperatures. As the moment of inertia is higher when a vibration is excited, the rotational constants (B) decrease. Consequently, the rotation frequencies in each vibration state are different from each other. This can give rise to "satellite" lines in the rotational spectrum. An example is provided by cyanodiacetylene, H−C≡C−C≡C−C≡N.
Further, there is a fictitious force, Coriolis coupling, between the vibrational motion of the nuclei in the rotating (non-inertial) frame. However, as long as the vibrational quantum number does not change (i.e., the molecule is in only one state of vibration), the effect of vibration on rotation is not important, because the time for vibration is much shorter than the time required for rotation. The Coriolis coupling is often negligible, too, if one is interested in low vibrational and rotational quantum numbers only.
Effect of rotation on vibrational spectra
Historically, the theory of rotational energy levels was developed to account for observations of vibration-rotation spectra of gases in infrared spectroscopy, which was used before microwave spectroscopy had become practical. To a first approximation, the rotation and vibration can be treated as separable, so the energy of rotation is added to the energy of vibration. For example, the rotational energy levels for linear molecules (in the rigid-rotor approximation) are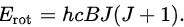
In this approximation, the vibration-rotation wavenumbers of transitions are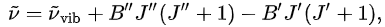
where B'' and B' are rotational constants for the upper and lower vibrational state respectively, while J'' and J' are the rotational quantum numbers of the upper and lower levels. In reality, this expression has to be modified for the effects of anharmonicity of the vibrations, for centrifugal distortion and for Coriolis coupling.
For the so-called R branch of the spectrum, J'=J''+1 so that there is simultaneous excitation of both vibration and rotation. For the P branch, J'=J''-1. so that a quantum of rotational energy is lost while a quantum of vibrational energy is gained. The purely vibrational transition, ΔJ=0, gives rise to the Q branch of the spectrum. Because of the thermal population of the rotational states the P branch is slightly less intense than the R branch.
Rotational constants obtained from infrared measurements are in good accord with those obtained by microwave spectroscopy, while the latter usually offers greater precision.
Structure of rotational spectra
Spherical top
Spherical top molecules have no net dipole moment. A pure rotational spectrum cannot be observed by absorption or emission spectroscopy because there is no permanent dipole moment whose rotation can be accelerated by the electric field of an incident photon. Also the polarizability is isotropic, so that pure rotational transitions cannot be observed by Raman spectroscopy either. Nevertheless, rotational constants can be obtained by ro-vibrational spectroscopy. This occurs when a molecule is polar in the vibrationally excited state. For example, the molecule methane is a spherical top but the asymmetric C-H stretching band shows rotational fine structure in the infrared spectrum, illustrated in rovibrational coupling. This spectrum is also interesting because it shows clear evidence of Coriolis coupling in the asymmetric structure of the band.
Linear molecules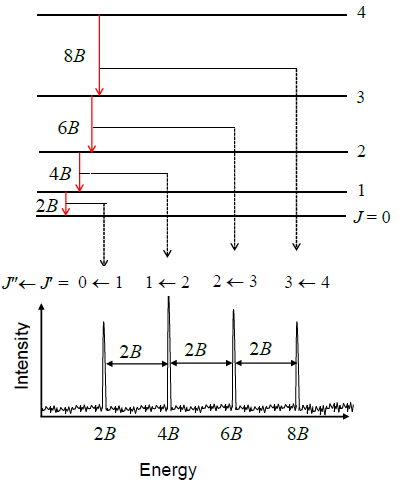 Energy levels and line positions calculated in the rigid rotor approximation
Energy levels and line positions calculated in the rigid rotor approximation
The rigid rotor is a good starting point from which to construct a model of a rotating molecule. It is assumed that component atoms are point masses connected by rigid bonds. A linear molecule lies on a single axis and each atom moves on the surface of a sphere around the centre of mass. The two degrees of rotational freedom correspond to the spherical coordinates θ and φ which describe the direction of the molecular axis, and the quantum state is determined by two quantum numbers J and M. J defines the magnitude of the rotational angular momentum, and M its component about an axis fixed in space, such as an external electric or magnetic field. In the absence of external fields, the energy depends only on J. Under the rigid rotor model, the rotational energy levels, F(J), of the molecule can be expressed as,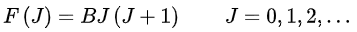
where B is the rotational constant of the molecule and is related to the moment of inertia of the molecule. In a linear molecule the moment of inertia about an axis perpendicular to the molecular axis is unique, that is, IB= IC, IA = 0, so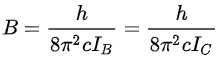
For a diatomic molecule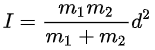
where m1 and m2 are the masses of the atoms and d is the distance between them.
Selection rules dictate that during emission or absorption the rotational quantum number has to change by unity; i.e., 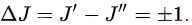 Thus, the locations of the lines in a rotational spectrum will be given by
Thus, the locations of the lines in a rotational spectrum will be given by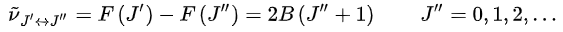
where J'' denotes the lower level and J' denotes the upper level involved in the transition.
The diagram illustrates rotational transitions that obey the ΔJ=1 selection rule. The dashed lines show how these transitions map onto features that can be observed experimentally. Adjacent J'' ← J' transitions are separated by 2B in the observed spectrum. Frequency or wavenumber units can also be used for the x axis of this plot.
Rotational line intensities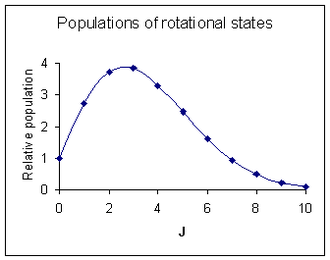 Rotational level populations with Bhc/kT = 0.05. J is the quantum number of the lower rotational stateThe probability of a transition taking place is the most important factor influencing the intensity of an observed rotational line. This probability is proportional to the population of the initial state involved in the transition. The population of a rotational state depends on two factors. The number of molecules in an excited state with quantum number J, relative to the number of molecules in the ground state, NJ/N0 is given by the Boltzmann distribution as
Rotational level populations with Bhc/kT = 0.05. J is the quantum number of the lower rotational stateThe probability of a transition taking place is the most important factor influencing the intensity of an observed rotational line. This probability is proportional to the population of the initial state involved in the transition. The population of a rotational state depends on two factors. The number of molecules in an excited state with quantum number J, relative to the number of molecules in the ground state, NJ/N0 is given by the Boltzmann distribution as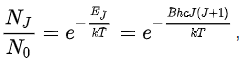
where k is the Boltzmann constant and T the absolute temperature. This factor decreases as J increases. The second factor is the degeneracy of the rotational state, which is equal to 2J + 1. This factor increases as J increases. Combining the two factors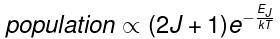
The maximum relative intensity occurs at
The diagram at the right shows an intensity pattern roughly corresponding to the spectrum above it.
Centrifugal distortion
When a molecule rotates, the centrifugal force pulls the atoms apart. As a result, the moment of inertia of the molecule increases, thus decreasing the value of B, when it is calculated using the expression for the rigid rotor. To account for this a centrifugal distortion correction term is added to the rotational energy levels of the diatomic molecule.
where D is the centrifugal distortion constant.
Therefore, the line positions for the rotational mode change to
In consequence, the spacing between lines is not constant, as in the rigid rotor approximation, but decreases with increasing rotational quantum number.
An assumption underlying these expressions is that the molecular vibration follows simple harmonic motion. In the harmonic approximation the centrifugal constant D can be derived as
where k is the vibrational force constant. The relationship between B and D
where  is the harmonic vibration frequency, follows. If anharmonicity is to be taken into account, terms in higher powers of J should be added to the expressions for the energy levels and line positions. A striking example concerns the rotational spectrum of hydrogen fluoride which was fitted to terms up to [J(J+1)]5.
is the harmonic vibration frequency, follows. If anharmonicity is to be taken into account, terms in higher powers of J should be added to the expressions for the energy levels and line positions. A striking example concerns the rotational spectrum of hydrogen fluoride which was fitted to terms up to [J(J+1)]5.
|
84 videos|142 docs|67 tests
|
FAQs on Rotational Spectroscopy - Physical Chemistry
| 1. What is rotational spectroscopy? |  |
| 2. How does rotational spectroscopy work? |  |
| 3. What are the applications of rotational spectroscopy? |  |
| 4. What are the advantages of rotational spectroscopy? |  |
| 5. What are some limitations of rotational spectroscopy? |  |





















