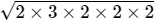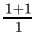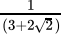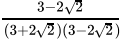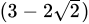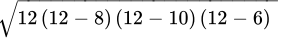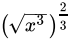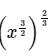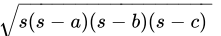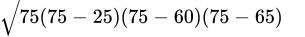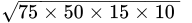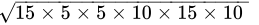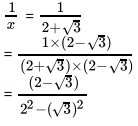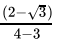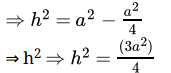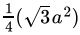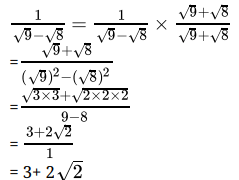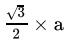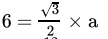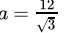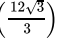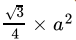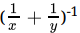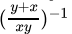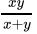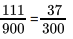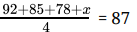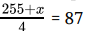Class 9 Math: Sample Question Paper Term I- 3 (With Solutions) | Mathematics (Maths) Class 9 PDF Download
| Table of contents |

|
| Class 09 Mathematics |

|
| Time: 90 Minutes |

|
| Max. Marks: 40 |

|
| Section - A |

|
| Section - B |

|
| Section - C |

|
Class 09 Mathematics
Time: 90 Minutes
Max. Marks: 40
General Instructions :
- The question paper contains three parts A, B and C
- Section A consists of 20 questions of 1 mark each. Attempt any 16 questions
- Section B consists of 20 questions of 1 mark each. Attempt any 16 questions.
- Section C consists of 10 questions based on two Case Studies. Attempt any 8 questions.
- There is no negative marking.
Section - A
Q.1: The value of xa-b x xb-c x xc-a is
(a) 1
(b) 2
(c) x
(d) 0
Correct Answer is Option (a)
xa-b x xb-c x xc-a
⇒ xa-b+b-c+c-a
⇒ x0
=1
Q.2: How many lines pass through two points?
(a) many
(b) three
(c) two
(d) only one
Correct Answer is Option (d)
only one because if a line is passing through two points then that two points are solution of a single linear equation
so only one line passes over two given points.
Q.3: The value of x in the figure is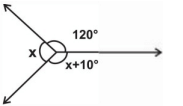
(a) 130°
(b) 100°
(c) 230°
(d) 115°
Correct Answer is Option (d)
Clearly, x + (x + 10) + 120 = 360⇒ 2x = 360 - 13
⇒ 2x = 230⇒ x = 115
Q.4: The area of one triangular part of a rhombus ABCD is given as 125 cm2. The area of rhombus ABCD is
(a) 1250 cm2
(b) 625 cm2
(c) 500 cm2
(d) 2500 cm2
Correct Answer is Option (c)
Since diagonals of a rhombus divide it into 4 x triangles of equal area. Therefore,
Area of rhombus = 4 x Area of triangle
= 4 x 125 = 500 sq. cm
Q.5: The decimal representation of a rational number is
(a) always terminating
(b) always non-terminating
(c) either terminating or repeating
(d) either terminating or non-repeating
Correct Answer is Option (c)
Rational numbers can be represented in decimal forms rather than representing in fractions. They can easily be represented as decimals by just dividing numerator ‘p’ by denominator ‘q’ (as rational numbers is in the form of p/q).
A rational number can be expressed as a terminating or nonterminating, recurring decimal.
Q.6: Express y in terms of x in the equation 5x - 2y = 7.
(a) 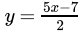
(b) 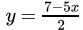
(c) 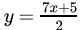
(d) 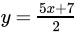
Correct Answer is Option (a)
5x - 2y = 7
- 2y = 7 - 5x
2y = 5x - 7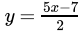
Q.7: If x > 0 and y < 0, then the point (x, -y) lies in ________.
(a) I quadrant
(b) II quadrant
(c) IV quadrant
(d) III quadrant
Correct Answer is Option (a)
I quadrant as x > 0, y < 0 then (x, -y) lies in Ist quadrant
Q.8: If ΔABC ≌ ΔLKM, then side of ΔLKM equal to side AC of ΔABC is
(a) KM
(b) LM
(c) LK
(d) None of these
Correct Answer is Option (b)
Since, by corresponding part of congruent triangle AC of ΔABC is equal to the LM of ΔLKM.
Q.9: √6 x √8 is equal to
(a) 6√8
(b) √14
(c) 4√3
(d) 3√4
Correct Answer is Option (c)
4√3
√6 x √8
= √6 x 8
=
= 4√3
Q.10: In ΔABC, ∠C = ∠A and BC = 6 cm and AC = 5 cm. Then the length of AB is:
(a) 2.5 cm
(b) 6 cm
(c) 5 cm
(d) 3 cm
Correct Answer is Option (b)
Sides opposite to equal angles are equal. Since, ∠C = ∠A , hence , AB=BC = 6 cm
Q.11: In Fig., which of the following statements must be true?
i. a + b = d + c
ii. a + c + e = 180°
iii. b + f = c + e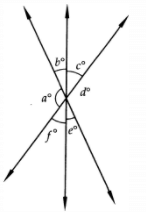
(a) (ii) only
(b) (i) only
(c) (ii) and (iii) only
(d) (iii) only
Correct Answer is Option (c)
Let AB, CD and EF intersect at O
∠AOD = ∠COB (Vertically opposite angle)
b = e (i)
∠EOC = ∠DOF (Vertically opposite angle)
f = c (ii)
Adding (i) and (ii), we get
b + f = c + e (iii)
Now,
∠ADE + ∠EOC + ∠COB = 180o
a + f + e = 180o
a + c + e = 180o [From (ii)]
Q.12: The value of 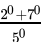 is
is
(a) 1/5
(b) 9/5
(c) 0
(d) 2
Correct Answer is Option (d)
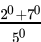
=
= 2
Q.13: 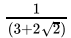 = ?
= ?
(a) 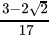
(b) 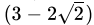
(c) 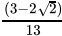
(d) None of these
Correct Answer is Option (b)
=
=
Q.14: Point (-7, 0) lies
(a) in the IV quadrant
(b) in the III quadrant
(c) on the negative direction of the y-axis
(d) on the negative direction of the x-axis
Correct Answer is Option (d)
(-a, 0) lies on the x-axis to the left (Negative direction of x-axis) of origin at a distance of 'a' units.
Q.15: For the equation 5x – 7y = 35, if y = 5, then the value of ‘x’ is
(a) 12
(b) -12
(c) -14
(d) 14
Correct Answer is Option (d)
For the equation 5x – 7y = 35, if y = 5,
5x - 7y = 35
y = 5
5x - 7.5 = 35
5x - 35 = 35
5x = 35 + 35
5x = 70
x = 70/5 = 14
x = 14
Q.16: In the adjoining figure, BC = AC. If ∠ACD = 115o, the ∠A is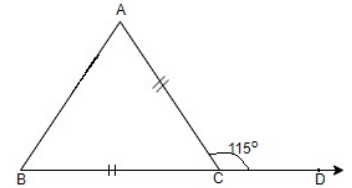
(a) 50o
(b) 65o
(c) 57.5o
(d) 70o
Correct Answer is Option (c)
As BC = AC, therefore triangle ABC is an isoscelestriangle.
Given ∠ACD = 115o, ∠ACB = 180 - 115 = 65o (Linear Pair)
As AC = BC, therefore ∠A = ∠B
As sum of all the three angles of atriangle is 180°
Therefore, ∠A +∠B +∠ACB = 180o
∠A = B = 57.5
Q.17: The edges of a triangular board are 6 cm, 8 cm and 10 cm. The cost of painting it at the rate of 70 paise per cm2 is
(a) ₹16.80
(b) ₹7
(c) ₹16
(d) ₹17.80
Correct Answer is Option (a)
S = 6 + 8 + 10 / 2 = 12 cm
A =
= 24 cm2
cost = 24 0.70 = ₹16.80
Q.18: Given the class intervals 1-10, 11-20, 21-30, …, then 20 is considered in class
(a) 11-20
(b) 21-30
(c) 15-25
(d) 11-30
Correct Answer is Option (a)
In a discontinuous class both lower and upper limits belong to that particular class.
Q.19: Which of the following is equal to ‘x’?
(a) 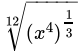
(b) 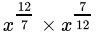
(c) 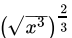
(d) 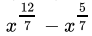
Correct Answer is Option (c)
=
= x
Q.20: The point O (0, 0) lies on:
(a) y-axis
(b) both x-axis and y-axis
(c) x-axis
(d) any quadrant
Correct Answer is Option (b)
Point (0, 0) is the co-ordinate of origin and origin is the point of intersection of x and y-axis. So, point O (0, 0) lies on both axis.
Section - B
Q.21: The linear equation 2x + 3y = 6 has
(a) two solutions
(b) a unique solution
(c) three solutions
(d) infinitely many solutions
Correct Answer is Option (d)
2x + 3y = 6
2x = 6 - 3y
x = 6-3y/2This table continues for infinte terms for different values of x & y. So for infinite value of y we have infinite value of x.
Therefore, this equation has Infinitely many solutions.
Q.22: The sides of a triangle are in the ratio 5 : 12 : 13 and its perimeter is 150 cm. The area of the triangle is
(a) 500 cm2
(b) 750 cm2
(c) 250 cm2
(d) 375 cm2
Correct Answer is Option (b)
Let the sides of the triangle be 5x cm, 12x cm and 13x cm.
Perimeter = Sum of all sides
or, 150 = 5x + 12x + 13x
or, 30x = 150
or, x = 5
Thus, the sides of the triangle are 5 x 5 cm, 12 x 5 cm and 13 x 5 cm, i.e., 25 cm, 60 cm and 65 cm.
Now,
Let:
a = 25 cm, b = 60 cm and c = 65 cm
s = 150/2 = 75cm
By Heron's formula, we have:
Area of triangle =
=
=
=
= 15 x 5 x 10
= 750 cm2
Q.23: The graph of y = x passes through the point?
(a) 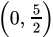
(b) (1, 1)
(c) 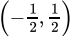
(d) 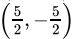
Correct Answer is Option (b)
y = x ⇒ Graph passes through (x, x) point. In particular for x = 1, y=1, hence, (1, 1) is the correct option.
Q.24: The sum of all the angles of a quadrilateral is
(a) 180o
(b) 360o
(c) 400o
(d) 320o
Correct Answer is Option (b)
Sum of the angles of a polygon = (n - 2) 180o
Quadrilateral has 4 sides,
So sum of interior angles = (4 - 2) 180o
= 360o
Q.25: If a = 2 + √3 then the value of 1/a is
(a) 2 + √3
(b) 2 - √3
(c) √3 - 2
(d) 1
Correct Answer is Option (b)
2 - √3
x = 2 + √3
=
= 2 - √3
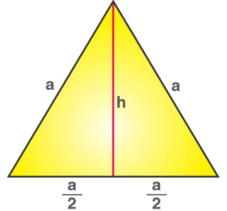
Q.26: Area of an equilateral triangle of side a unit is
(a) √3/2a
(b) √3/2a2
(c) √3/4a2
(d) √3/4a
Correct Answer is Option (c)
Now,Area of Triangle = 1/2 x base x height
Here, base = a, and height = h
Now, apply Pythagoras theorem in the triangle.
a2 = h2 + (a/2)2
Or, h = 1/2(√3a)
Now, put the value of “h” in the area of the triangle equation.
So, Area of Triangle = 1/2 x base x height
⇒
Or, Area of Equilateral triangle =
Q.27: The following marks were obtained by the students in a test:
81, 72, 90, 90, 86, 85,92, 70, 71, 83, 89, 95,85, 79, 62
The range of the marks is
(a) 9
(b) 33
(c) 27
(d) 17
Correct Answer is Option (b)
Range of observations = Highest observation - Lowest observation|
= 95 - 62 = 33
Q.28: 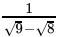 is equal to
is equal to
(a) 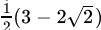
(b) 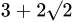
(c) 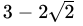
(d) 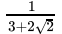
Correct Answer is Option (b)
After rationalising:
Q.29: In ΔABC, BD ⊥ AC, CAE = 30° and CBD = 40°. Then AEB =?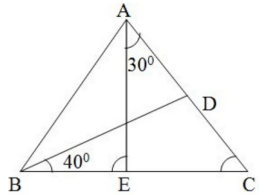
(a) 70°
(b) 60°
(c) 50°
(d) 80°
Correct Answer is Option (d)
In BDC
∠BDC + ∠BCD + ∠DBC = 180°
BD ⊥ AC
∠BCD = 90°, ∠DBC = 40°
90° + ∠BCD + 40° = 180°
∠BCD + 130° = 180°
∠BCD = 180° - 130°
∠BCD = 50°
∠AEB = ∠CAE + ∠C ...(exterior angle)
∠CAE = 30°
∠C = 50°
∠AEB = 30° + 50°
∠AEB = 80°
Q.30: In a frequency distribution, ogives are graphical representation of
(a) Cumulative frequency
(b) Frequency
(c) Relative frequency
(d) Raw data
Correct Answer is Option (a)
An o-give (oh-jive), sometimes called a cumulative frequency polygon, is a type of frequency polygon that shows cumulative frequencies. An o-give graph plots cumulative frequency on the y-axis and class boundaries along the x-axis.
Q.31: The height of an equilateral triangle is 6 cm, Then the area of the triangle i
(a) 17√3 cm2
(b) 12√3cm2
(c) 3√3cm2
(d) 9√3cm2
Correct Answer is Option (b)
Let each side of an equilateral triangle be 'a' units.
∴ its height =
∴
∴
=..... (Rationalizing the denominator)
=
= 4√3 cm
∴ each side of an equilateral = 4√3 cm
∴ Area =
=
= 12√3cm2
Q.32: When simplified (x-1 + y-1)-1 is equal to
(a) xy
(b) x + y
(c) xy / x + y
(d) x + y / xy
Correct Answer is Option (c)
(x-1 + y-1)-1
=
=
=
Q.33: If the bisector of the angle A of a ABC is perpendicular to the base BC of the triangle then the triangle ABC is:
(a) Isosceles
(b) Obtuse Angled
(c) Equilateral
(d) Scalene
Correct Answer is Option (c)
Angle bisector is perpendicular to the opposite side only in equilateral triangle.
Q.34: For the frequency distribution given below, the adjusted frequency for the class 25-45 is: (a) 2
(a) 2
(b) 3
(c) 6
(d) 5
Correct Answer is Option (a)
Adjusted frequency for the class 25-45 is 10 - 8 = 2
Q.35: In the figure, measure of ∠B is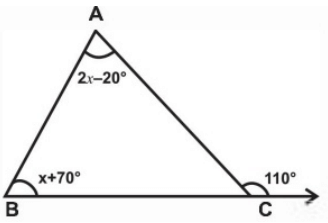
(a) 70°
(b) 20°
(c) 90°
(d) 110°
Correct Answer is Option (c)
we have, 2x - 20o + x + 70o = 110o
3x = 110o- 50o = 60o
⇒ x = 2o
∠B = x + 70 = 90o
Q.36: If we multiply both sides of a linear equation with a non-zero number, then the solution of the linear equation:
(a) Remains the same
(b) Changes in case of multiplication only
(c) Changes in case of division only
(d) Changes
Correct Answer is Option (a)
If for any c. where c is any natural number
Like addition and subtraction we can multiply and divide both sides of an equation by a number, c, without changing the equation, where c is any natural number.
Q.37: The perimeter of a triangle is 36 cm and its sides are in the ratio a : b : c = 3 : 4 : 5 then a, b, c are respectively:
(a) 12 cm, 9 cm, 15 cm
(b) 15 cm, 12 cm, 9 cm
(c) 9 cm, 15 cm, 12cm
(d) 9 cm, 12 cm, 15 cm
Correct Answer is Option (d)
Let the three sides a, b, c be 3x, 4x and 5x respectively.
Then according to the conditions given in the question, we have
3x + 4x + 5x = 36
12x = 36
x = 3 cm
Thus, the three sides are :
a = 3 x 3 = 9 cm, b = 4 x 3 = 12 cm and c = 5 x 3 = 15 cm
Q.38: The simplest form of 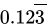 is
is
(a) none of these
(b) 37 / 330
(c) 41 / 330
(d) 41 / 333
Correct Answer is Option (a)
Since=
Q.39: In a histogram, which of the following is proportional to the frequency of the corresponding class?
(a) Width of the rectangle
(b) Length of the rectangle
(c) Perimeter of the rectangle
(d) Area of the rectangle
Correct Answer is Option (d)
In, Histogram each rectangle is drawn, where width equivalent to class interval and height equivalent to the frequency of the class.
Since class interval are same across the distribution table, area of the rectangle is corresponding to frequency or height of the rectangle
Q.40: Vihaan has marks of 92, 85, and 78 in three mathematics tests. In order to have an average of exactly 87 for the four math tests, he should obtain
(a) 93 marks
(b) 91 marks
(c) 90 marks
(d) 92 marks
Correct Answer is Option (a)
Let, Vihaan obtains x marks in the fourth test.
So,
255 + x = 348
x = 348 - 255
x = 93 marks
Section - C
Question No. 41 to 45 are based on the given text. Read the text carefully and answer the questions:
In a forest, a big tree got broken due to heavy rain and wind. Due to this rain the big branches AB and AC with lengths 5m fell down on the ground. Branch AC makes an angle of 30° with the main tree AP. The distance of Point B from P is 4 m. You can observe that ΔABP is congruent to ΔACP.
Q.41: ΔACP and ΔABP are congruent by which criteria?
(a) SAS
(b) ASA
(c) RHS
(d) SSS
Correct Answer is Option (c)
RHS
Q.42: What is the length of CP?
(a) 3 m
(b) 4 m
(c) 10 m
(d) 5 m
Correct Answer is Option (b)
4 m
Q.43: What is the value of ∠BAP?
(a) 40°
(b) 30°
(c) 50°
(d) 60°
Correct Answer is Option (b)
30°
Q.44: What is the value of ∠APB?
(a) 40°
(b) 50°
(c) 60°
(d) 90°
Correct Answer is Option (d)
90°
Q.45: What is the height of the remaining tree?
(a) 3 m
(b) 5 m
(c) 4 m
(d) 10 m
Correct Answer is Option (a)
3 m
Question No. 46 to 50 are based on the given text. Read the text carefully and answer the questions: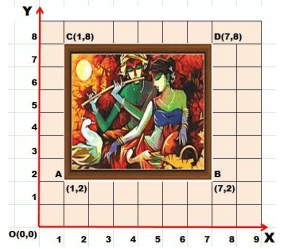 Rohit was putting up one of his paintings in his living room. Before this Rohit had put a grid on the wall where each unit measured equal to a foot. The upper-left corner of the frame is at point C (1, 8) and the upper-right corner at D (7, 8). The bottom-left corner is at A (1, 2) and the bottom-right corner at B (7, 2).
Rohit was putting up one of his paintings in his living room. Before this Rohit had put a grid on the wall where each unit measured equal to a foot. The upper-left corner of the frame is at point C (1, 8) and the upper-right corner at D (7, 8). The bottom-left corner is at A (1, 2) and the bottom-right corner at B (7, 2).
Q.46: What is the width of the painting plus frame?
(a) 6 feet
(b) 9 feet
(c) 8 feet
(d) 5 feet
Correct Answer is Option (a)
6 feet
Q.47: What is the length of the painting plus frame?
(a) 6 feet
(b) 9 feet
(c) 8 feet
(d) 5 feet
Correct Answer is Option (a)
6 feet
Q.48: Which sides of the painting are parallel to x-axis?
(a) Diagonals AD and BC
(b) AB and CD
(c) AC and BD
(d) No one
Correct Answer is Option (b)
AB and CD
Q.49: Which sides of the painting are parallel to y-axis?
(a) No one
(b) Diagonals AC and BD
(c) AB and CD
(d) AC and BD
Correct Answer is Option (d)
AC and BD
Q.50: Point A, B, C and D lie in which quadrant?
(a) II
(b) III
(c) I
(d) IV
Correct Answer is Option (c)
I
|
40 videos|471 docs|57 tests
|