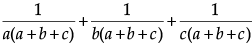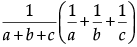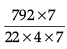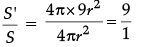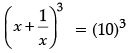Class 9 Math: Sample Question Paper Term II - 1 (With Solutions) | Mathematics (Maths) Class 9 PDF Download
| Table of contents |

|
| Class IX Mathematics |

|
| Time: 120 Minutes |

|
| Max. Marks: 40 |

|
| Section - A |

|
| Section - B |

|
| Section - C |

|
Class IX Mathematics
Time: 120 Minutes
Max. Marks: 40
General Instructions :
- The question paper consists of 14 questions divided into 3 sections A, B and C.
- All questions are compulsory.
- Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.
- Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one question.
- Section C comprises of 4 questions of 4 marks each. An internal choice has been provided in one question. It contains two case study based questions.
Section - A
Q.1: Two coins are tossed simultaneously 500 times, following are the outcomes
No head= 100 times
One head = 200 times
Two heads = 200 times
If the two coins are simultaneously tossed again, compute the probability of obtaining:
(i) One Head
(ii) Two Heads
Total number of outcomes, n(S) = 500
Let E1 and E2 be the events of one head and two heads respectively.
(i) Favourable outcomes n(E1) = 200
Then, P(one head) = n(E1)/n(S)
P(one head) = 200/500= 2/5
(ii) Favourable outcomes n(E2) = 200
Then, P(Two heads) = n(E2)/n(S)
P(E2) = 200/500 = 2/5
Q.2: Factorize: 64a3 – 27b3 – 144a2b + 108ab2
OR
Find the value of k, so that polynomial x3 + 3x2 – kx – 3 has one factor as x + 3.
64a3 – 27b3 – 144a2b + 108ab2
= (4a)3 – (3b)3 – 3 × (4a)2 × (3b) + 3 × (4a) × (3b)2
[Using identity, x3 – y3 – 3x2y + 3xy2 = (x – y)3]
= (4a – 3b)3OR
Let f(x) = x3 + 3x2 – kx – 3
Since, (x + 3) is a factor of f(x).
Then, f(– 3) = 0
or, (– 3)3 + 3(– 3)2 – k(–3) – 3 = 0
or, – 27 + 27 + 3k – 3 = 0
or, 3k – 3 = 0
or, k = 1.
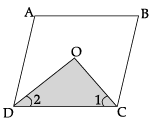
Q.3: In a parallelogram, show that the angle bisectors of two adjacent angles intersect at right angle.
Let ABCD be a parallelogram, then
∠ADC + ∠BCD = 180° [Co-interior angles]
or, 1/2 ∠ADC + 1/2 ∠BCD = 90° [Divide by 2]
or ∠2 + ∠1 = 90°
In Δ ODC,
∠1 + ∠2 + ∠DOC = 180° [Angle sum property of a triangle]
∴ ∠DOC = 90°.
Hence, the angle bisectors of two adjacent angles intersect at 90°.
Q.4: The angles of a quadrilateral are 4x°, 7x°, 15x° and 10x°. Find the smallest and largest angles of the quadrilateral.
Sum of the angles of a quadrilateral is 360°.
∴ 4x° + 7x° + 15x° + 10x° = 360°
or, 36x° = 360°
or, x° = 10°
∴ Smallest angle = 4x° = 4 × 10° = 40°
Largest angle = 15x° = 15 × 10°
= 150°
Q.5: A coin is tossed 1200 times with the following outcomes:
Head: 455, Tail: 745
Compute the probability for: (i) getting head, (ii) getting tail.
(i) Number of favorable outcomes n(A) = 455
Total outcomes n(S) = 455 + 745 = 1200
Probability of getting head = n(A) / n(S)= 455/1200 = 91/240
(ii) Number of favourable outcomes n(B) = 745
Total outcomes n(S) = 1200
Probability of getting tail = n(B)/n(S)
= 745/1200 = 149/240
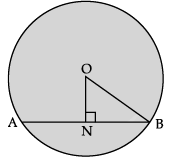
Q.6: A chord of length 10 cm is at a distance of 12 cm from the centre of a circle. Find the radius of the circle.
OR
In the given figure, find the value of x.
Let AB be the chord of a circle and ON be the distance of the chord from the centre.
Given, AB = 10 cm
ON = 12 cm
Also, ON ⊥ AB
and AN = BN
[Q Perpendicular drawn from the centre of the circle to chord of circle bisects the chord]
In Δ ONB,
OB2 = ON2 + NB2[By Pythagoras theorem]
∴ OB2 = 122 + 52 [∵ BN = 5 cm]
= 144 + 25 = 169
∴ OB = 13 cm
Hence, the radius of the circle is 13 cm.OR
Here, ABCD is a cyclic quadrilateral.
In a cyclic quadrilateral,
∠A + ∠C = 180° [opposite angles of cyclic quadrilateral are supplementary]
or, 2x + 4° + 4x – 64° = 180°
or, 6x – 60° = 180°
or, 6x = 180° + 60° = 240°
or, x = 240°/6
∴ x = 40°
Section - B
Q.7: Find the value of k, if x – 2 is a factor of f(x) = x2 + kx + 2k. Also find the factorise of f(x), when putting the value of k.
Given, (x – 2) is a factor of f(x).
∴ f(2) = 0
or, (2)2 + k(2) + 2k = 0
or, 4 + 2k + 2k = 0
or, 4 + 4k = 0
or, k = – 1
So, f(x) = x2 + (–1)x + 2(–1)
= x2 – x – 2
= x2 – 2x + x – 2
= x(x – 2) + 1(x – 2)
= (x – 2)(x + 1)
Q.8: Verify if – 2 and 3 are zeroes of the polynomial 2x3 – 3x2 – 11x + 6. If yes, factorize the polynomials.
Let p(x) = 2x3 – 3x2 – 11x + 6
For, x = – 2
p(– 2) = 2(– 2)3 – 3(– 2)2 – 11(– 2) + 6
= – 16 – 12 + 22 + 6
= – 28 + 28 = 0
For, x = 3
p(3) = 2(3)3 – 3(3)2 – 11(3) + 6
= 54 – 27 – 33 + 6
= 60 – 60 = 0
So, – 2 and 3 are zeroes of the given polynomial.
Now, p(x) = 2x3 – 3x2 – 11x + 6
(x + 2)(x – 3) = x2 – x – 6 is a factor of p(x).
∴ 2x3 – 3x2 – 11x + 6
= 2x3 + 4x2 – 7x2 – 14x + 3x + 6
= 2x2(x + 2) – 7x(x + 2) + 3(x + 2)
= (x + 2)(2x2 – 7x + 3)
= (x + 2)(2x2 – 6x – x + 3)
= (x + 2)[(2x(x – 3) – 1(x – 3)]
= (x + 2)(x – 3)(2x – 1)
Q.9: If ab + bc + ca = 0, then find the value of 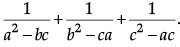
ab + bc + ca = 0 ...(i)
⇒ – bc = ab + ca ...(ii)
– ca = ab + bc ...(iii)
and – a b = bc + ca ...(iv)
Now,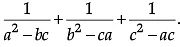
=[Using (i), (iii) & (iv)]
=
=
=[Using (i)]
= 0
Q.10: Find the radius of the base of a right circular cylinder whose curved surface area is 2/3
of the sum of the surface areas of two circular faces. The height of the cylinder is given to be 15 cm.
OR
The radius and slant height of a cone are in the ratio 4: 7. If its curved surface area is 792 cm2, find its radius.
Let the radius and height of the cylinder be r and h respectively, then
h = 15 cm [given]
C.S.A. of the cylinder = 2/3 (Sum of areas of 2 circular faces)
2πrh = 2/3(2πr2)
h = 2/3r
15 = 2/3r
or, r = 22.5 cm.OR
Let the radius of cone be r = 4x
and slant height l = 7x
∵ CSA of a cone = 792 cm2
∴ πrl = 792
or, 22/7 x 4x x 7x = 792
x2 =
= 9
or, x = 3
∴ radius = 4 × 3
= 12 cm.
Section - C
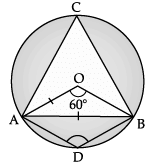
Q.11: A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
According to the question,
OA = AB = OB
∴ ΔOAB is an equilateral triangle
i.e., ∠AOB = 60°
∠ACB = 1/2 ∠AOB
[angle subtended by an arc at the circumference is half of the angle at the centre of circle]
∠ACB = 1/2 x 60°
∠ACB = 30°
∠ACB + ∠ADB = 180°
[opposite angles of cyclic quadrilateral are supplementary]
or, ∠ADB = 180° – ∠ACB
∠ADB = 180° – 30°
= 150°
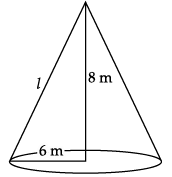
Q.12: What length of tarpaulin 3 m wide will be required to make conical tent of height 8 m and base radius 6 m ? Assume that the extra length of material that will be required for stitching margins and wastage in cutting is approximately 20 cm (Use π = 3.14).
OR
Twenty-seven solid iron spheres, each of radius r and surface area S are melted to form a sphere with surface area S'. Find the (i) radius R' of the new sphere, (ii) ratio of S' and S.
Given, Conical tent: height (h) = 8 m
base radius (r) = 6 m
l2 = r2 + h2
l2 = 82 + 62
l = √64 +36 = √100 = 10 cm
C.S.A of tent = πrl unit2
= 3.14 × 6 × 10 m2
= 188.4 m2
Area of Tarpaulin = C.S.A of tent width × length of tarpaulin = 188.4 m2
3 × length of tarpaulin = 188.4 m2
length of tarpaulin = 188.4/3
= 62.8 m
Extra length required for stitching and wastage of cutting
= 20 cm = 0.20 m
∴ Total length of tarpaulin
= 62.8 + 0.2
= 63 mOR
Given: radius of each sphere = r
Volume of 1 solid iron sphere = 4/3πr3
Volume of 27 solid iron spheres = 4/3πr3 x 27
Volume of new sphere = 4/3 x 27πr3
Let radius of now sphere be R, then according to given condition,
Volume of new sphere made after melting 27 spheres = Volume of 27 spheres
4/3πR3 = 4/3 x 27πr3
R3 = 27r3
(i) R = 3r unit
(ii) Surface area of new sphere = 4πR2
S' = 4π × (3r)2
S' = 4π × 9r2 unit2
Surface area of Sphere (S) = 4πr2
Now,
S' : S = 9 : 1
Case Study-1
Q.13: Read the following text and answer the following questions on the basis of the same: Beti Bachao, Beti Padhao (BBBP) is a personal campaign of the Government of India that aims to generate awareness and improve the efficiency of welfare services intended for girls. In a school, a group of (x + y) teachers, (x2 + y2) girls and (x3 + y3) boys organised a campaign on Beti Bachao, Beti Padhao.
In a school, a group of (x + y) teachers, (x2 + y2) girls and (x3 + y3) boys organised a campaign on Beti Bachao, Beti Padhao.
(i) If in the group, there are 10 teachers and 58 girls, then what is the number of boys?
(ii) If x – y = 23, then find x2 – y2.
(i) No. of teachers= x + y = 10
⇒ (x + y)2 = (10)2
⇒ x2 + y2 + 2xy = 100 ...(i)
No. of girls = (x2 + y2) = 58
⇒ 58 + 2xy = 100 ...using equation (i)
⇒ 2xy = 100 – 58
⇒ 2xy = 42
⇒ xy = 42/2
⇒ xy = 21
Now, since (x + y)3 = [x3 + y3 + 3xy(x + y)]
⇒ (10)3 = [x3 + y3 + 3 × 21(10)]
⇒ 1000 = (x3 + y3 + 630)
⇒ 1000 – 630 = (x3 + y3)
⇒ (x3 + y3) = 370
Hence, no. boys = 370
(ii) Given x – y = 23
Also, x + y = 10 [Taking from part (i)]
x2 – y2 = (x + y) (x – y)
= 10 × 23 = 230
Hence, the value of x2 – y2 is 230.
Case Study-2
Q.14: Read the following text and answer the questions given below: National Association for the Blind (NAB) aimed to empower and well-inform visually challenged population of our country, thus enabling them to lead a life of dignity and productivity. Ravi donated ₹
Ravi donated ₹ 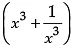 to NAB. When his cousin asks to tell the amount donated by him, he just gave ,the hint. x + 1/x = 10
to NAB. When his cousin asks to tell the amount donated by him, he just gave ,the hint. x + 1/x = 10
(i) Find the amount donated by Ravi.
(ii) Find the amount donated by Ravi if x + 1/x =7
(i)
= 1000
[Use formula : (a + b)3 = a3 + b2 + 3ab(a + b)]= 1000
= 1000 - 30 = 970
Hence, amount donated by Ravi = ₹ 970.
(ii) Given: x + 1/x =7
Taking cube on both sides, we get= 343
= 343
= 343 – 21 = 322.
Hence, amount donated by Ravi = ₹322.
|
40 videos|560 docs|57 tests
|
FAQs on Class 9 Math: Sample Question Paper Term II - 1 (With Solutions) - Mathematics (Maths) Class 9
| 1. What is the duration of the Class IX Mathematics exam? |  |
| 2. How many marks is the Class IX Mathematics exam out of? |  |
| 3. How many sections are there in the Class IX Mathematics exam? |  |
| 4. What is the difficulty level of the questions in the Class IX Mathematics exam? |  |
| 5. What is the purpose of Section C in the Class IX Mathematics exam? |  |