Number System in Computers | Computer Science for Class 7 PDF Download
Introduction
A set of values used to represent different quantities is known as Number System. For example, a number system can be used to represent the number of students in a class or number of viewers watching a certain TV program etc. The digital computer represents all kinds of data and information in binary numbers. It includes audio, graphics, video, text and numbers. The total number of digits used in a number system is called its base or radix. The base is written after the number as subscript.Some important number systems are as follows.
- Decimal number system
- Binary number system
- Octal number system
- Hexadecimal number system
Decimal number System
The Decimal Number System consists of ten digits from 0 to 9. These digits can be used to represent any numeric value. The base of decimal number system is 10. It is the most widely used number system. The value represented by individual digit depends on weight and position of the digit.
Binary Number System
Digital computer represents all kinds of data and information in the binary system. Binary Number System consists of two digits 0 and 1. Its base is 2. Each digit or bit in binary number system can be 0 or 1. A combination of binary numbers may be used to represent different quantities like 1001. The positional value of each digit in binary number is twice the place value or face value of the digit of its right side. The weight of each position is a power of 2.
Octal Number System
Octal Number System consists of eight digits from 0 to 7. The base of octal system is 8. Each digit position in this system represents a power of 8. Any digit in this system is always less than 8. Octal number system is used as a shorthand representation of long binary numbers. The number 6418 is not valid in this number system as 8 is not a valid digit.
Hexadecimal Number System
The Hexadecimal Number System consists of 16 digits from 0 to 9 and A to F. The alphabets A to F represent decimal numbers from 10 to 15. The base of this number system is 16. Each digit position in hexadecimal system represents a power of 16. The number 76416 is valid hexadecimal number. It is different from 76410 which is seven hundred and sixty four. This number system provides shortcut method to represent long binary numbers.
The place where the digit is placed have it own value called place value .
- Place value= (base).
- To understand this let us take an example of the decimal number system.
- Consider a number 512.
Now the place value of digit 5 is (10)2 . Here 10 is the base and 2 is the place ( Note place is counted from the right starting from 0 ).
- Similarly place value of digit 1 is (10)1 i.e. -10
- Place value of digit 2 is (10)2 i.e.-1
- So the number 512 = 5 × 102 + 5 × 101 + 5 × 100
Conversion of binary to decimal
(i) 1) (1101)2 → (x)10(NOTE: Place value is counted from the right starting with zero.)
13 (sum step 3 which is decimal)
(ii) (100101)2 → (x)10
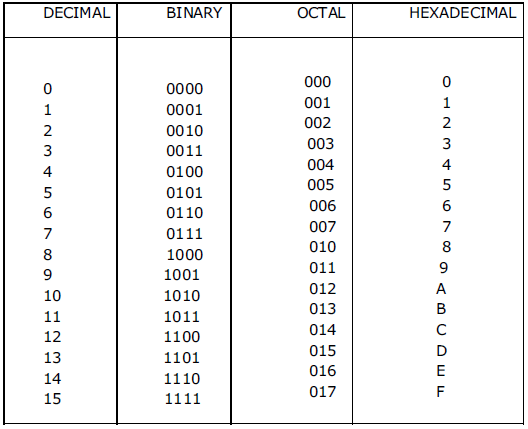
Conversion of octal to decimal
(i) (327)8 → (x)10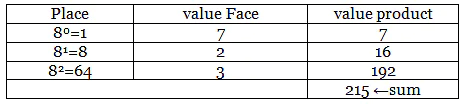 (ii) (A B 4 )16 → (x)10
(ii) (A B 4 )16 → (x)10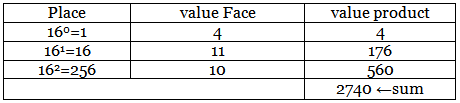
Conversion of Decimal to another base.
Step 01 divide the decimal number by the base of the number system to be formed.
Step 02 The remainder is the right most digit of new number system.
Step 03 divide the quotient of the previous division by the base. Step 04 Repeat the process till the quotient becomes zero.
Note: The right most digit of any number system is called as least significant digit. The left most digit of any number system is called as most significant digit.
- If the number system is binary.
- Right most digit is called Last Significant Bit (LSB).
- Left most digit is called Most Significant Bit ( MSB ).
Logic Gates
It is an electronic circuit that has one or more input signal s and produces a single output signals. It is building block of all electronic circuits in a computer.- AND, OR and NOT are the basic gate.
AND gate:
- It performs logical multiplication
- The output of AND gate is 1, only if all input signal are 1
Let A and B be the inputs then the output ≥= A.B
Truth Table: Truth Table gives the relation between the input and output.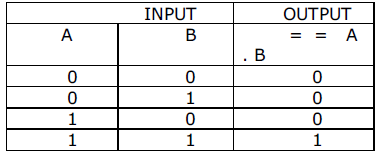
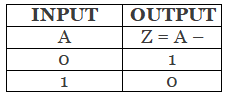
Not Gate
- It is also know as inverter gate because it invents the input.
- It performs complement operation i.e. if the input is 1 . the output is 0 & if input is 0 then output is 1
- Apart from 3 basic gate i.e. AND , OR , and NOT that we have studied there are 2 universal gate NAND and NOR.
- NAND and NOR are called the universal gate because each and every gate can be built using these gates.
NAND gate
- It is complemented AND gate.
- The output of NAND gate is 0 . Only if all input singal are and output will be 1 if any one of input is o .
Let A & B be the input than the output z = A . B
|
26 docs|14 tests
|





















