The Triangle and Its Properties Class 7 Notes Maths Chapter 6
Triangles
A triangle is a basic shape you see in many places. It is a simple closed figure made up of three straight line segments.
 Triangle we see in everyday life
Triangle we see in everyday life
So, in small-small things around us we see triangles. Triangle is a very common geometrical shape we use in day to day life.
A triangle has: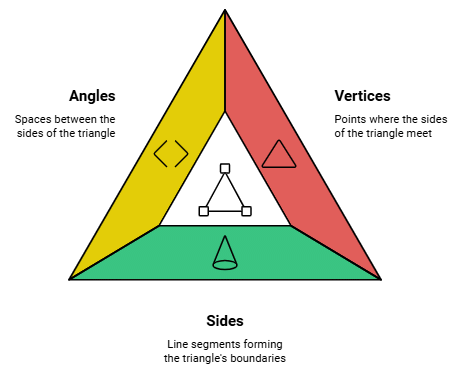
- Three Vertices: The points where the sides meet (like points A, B, and C in triangle ∆ABC).
- Three Sides: The line segments that form the triangle (AB, BC, and CA).
- Three Angles: The space between the sides (∠BAC, ∠ABC, and ∠BCA).

Triangles can be classified in two main ways:
Based on Sides:
- Scalene Triangle: All sides are different lengths.
- Isosceles Triangle: Two sides are of equal length.
- Equilateral Triangle: All three sides are equal in length.
Based on Angles:
- Acute-Angled Triangle: All angles are less than 90º
- Obtuse-Angled Triangle: One angle is greater than 90º
- Right-Angled Triangle: One angle is exactly 90º
So, in small-small things around us we see triangles. Triangle is a very common geometrical shape we use in day to day life.
Medians of a Triangle
Let's understand with an example; Suppose there are 6 members in Kartik’s family and he has only one triangular piece of pizza.
Now, Kartik wants to divide this piece of pizza equally among all the family members. So, how will Kartik divide this piece of pizza?
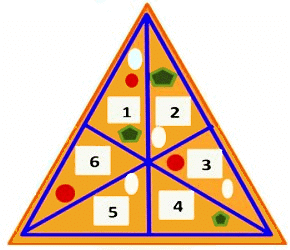
So, Kartik will divide the piece of pizza into six equal pieces by cutting along the lines as shown in the above figure.
What are these lines called?
These lines are nothing but the medians of a triangle. A line segment drawn from any vertex of the triangle to the mid-point of the opposite sides of a triangle is called a median.
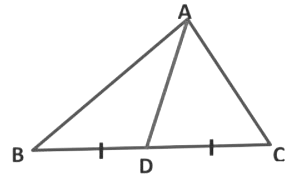
In triangle ABC, segment AD is the median of the triangle because one of its endpoints A is the vertex of the triangle and his other endpoint D is the midpoint of its opposite side BC.
Triangle has three vertices. So, we can draw three medians to each triangle from each vertex.
Perpendicular bisector: A perpendicular bisector is a segment, line, or ray that is perpendicular to a segment at its midpoint.
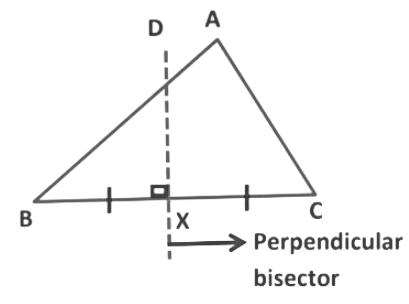
In triangle ABC, DX is the perpendicular bisector of segment BC because it is perpendicular to segment BC at its midpoint X.
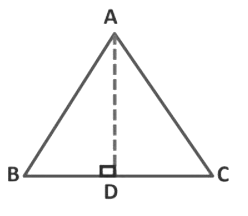
Altitudes of a Triangle
Altitude of a triangle is a perpendicular line segment that joins a vertex of the triangle to the opposite side.
- Triangle ABC has segment AD as an altitude.
- Endpoint A is the vertex of the triangle.
- Endpoint D of segment AD is on the opposite side of the triangle.
- Segment AD is perpendicular to the opposite side BC.
- Each triangle has a total of three vertexes.
- We can draw a maximum of three altitudes in each triangle.
- The altitudes are shown in the adjacent figure.
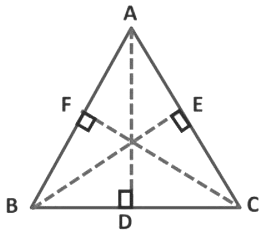
An altitude of a triangle can be inside or may lie outside the triangle.
Note: These all perpendicular are nothing but the altitudes of the triangle.
Example 1: Draw the altitude and median in the given triangle from vertex A.
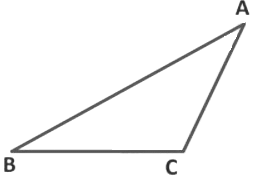
Sol: In the given triangle ABC to draw a median first we find the mid-point of segment BC then join it with vertex A.
Also, we know the altitude of a triangle is a perpendicular line segment that joins a vertex of the triangle to the opposite side.
Hence, to draw altitude first we extend the side BC then we draw the perpendicular from vertex A.
Exterior Angle of Triangle and Its Properties
In the earlier chapter, we see angles that are present inside the triangle. Now, we talk about angles that are present outside of the triangle, and they are called exterior angle.

In the above ΔABC we see, ∠1, ∠2 and ∠3 is present inside the triangle, so we called it as interior angles of a triangle.
So, if we extend the BC to D observe ∠4 is formed at point C. This angle lies in the exterior of ΔABC. We call it the exterior angle of the ΔABC.
Angle is formed between one side of a triangle and extended adjacent side, so we say that an exterior angle is an angle between one side of a triangle and an extended adjacent side.
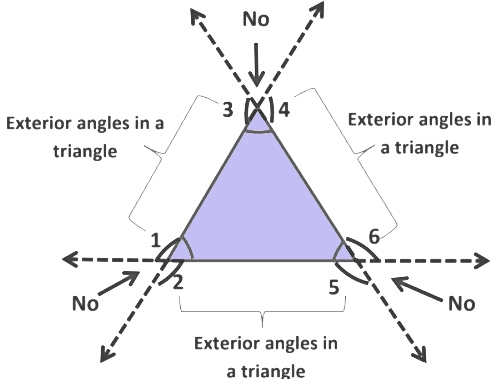
We know there are three sides of the triangle and when we extend these sides six exterior angles are formed.

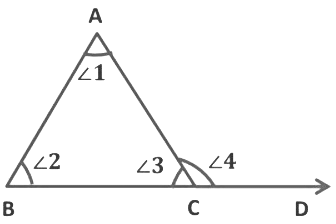
To prove: Sum of interior opposite angles are equal to an exterior angle.
i.e ∠1 + ∠2 = ∠4
In the figure we see, ∠3 and ∠4 are adjacent angles. ∠4 is exterior angle and ∠1 and ∠2 are Interior opposite angles of ∠4
Draw a line EF parallel to AB which is passing through C. Line EF divide ∠4 into two angles ∠ECA marked as ∠5 and ∠ECD marked as ∠6
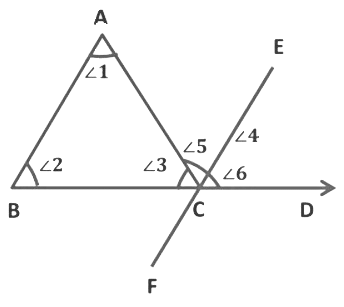
∠5 + ∠6 = ∠4 ... (i)
∠1 = ∠5 AB||EF and AC is a transversal line
(Alternate interior angles are equal)... (ii)
∠2 = ∠6 AB||EF and BD is a transversal line
(Corresponding angles are equal)... (iii)
By adding (ii) and (iii) we get
∠1 + ∠2 = ∠5 + ∠6
From equation (i)
∠1 + ∠2 = ∠4
Example: In the given figure, find ∠ACD
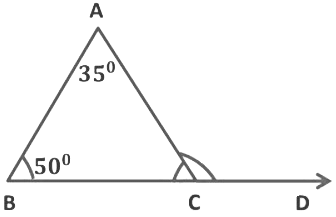
Sol: For ΔABC, ∠ACD, is an exterior angle. ∠ABC, ∠BAC are interior opposite angles.
We know, an exterior angle of a triangle is equal to the sum of its interior opposite angles.
∴ ∠ACD = ∠ABC + ∠BAC
∴ ∠ACD = 50° + 35°
∴ ∠ACD = 85°
Example: Exterior angle ∠ACD = 100° and ∠ABC and ∠ACB are in the ratio of 3: 2. Find ∠ABC and ∠BAC of the triangle.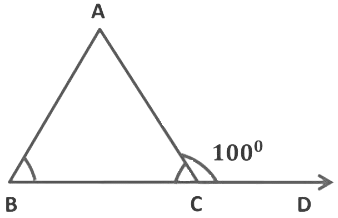
Sol: Let, ∠ABC = 3x and ∠ACB = 2x
We know, an exterior angle of a triangle is equal to the sum of its interior opposite angles.
∴ ∠ACD = ∠ABC + ∠ACB
∴ 100° = 3x + 2x
∴ 100° = 5x∴ x = 100°/5
∴ x = 20°→ ∠ABC = 3x = 3 × 20° = 60°
→ ∠ACB = 2x = 2 × 20° = 40°
Angle Sum Property of Triangle
The sum of the interior angles of a triangle is 180°. This property of a triangle is true for all triangles.
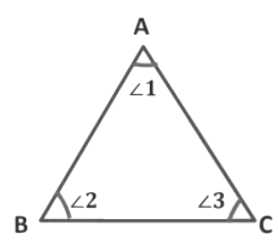
In ΔABC, ∠1, ∠2, and ∠3 are the interior angles of a triangle.
To prove: Sum of the interior angles of a triangle is 180°.
∠1 + ∠2 + ∠3 = 180°
Construction: Extend side BC to D we get exterior ∠4
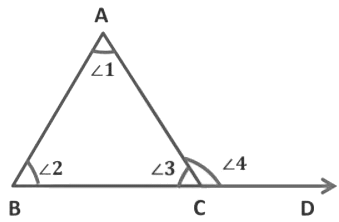
∠1, ∠2 and ∠3are angles of ΔABC. ∠4is the exterior angle when BC is extended to D.
∠1 + ∠2 = ∠4 ... (By exterior angle property)
Adding ∠3 to both the side
∠1 + ∠2 + ∠3 = ∠4 + ∠3
But, ∠4 and ∠3 form a linear pair
So,
∠4 + ∠3 = 180°... (Linear pair)
Therefore,
∠1 + ∠2 + ∠3 = 180°
Hence, proved
Example: In ∆ABC, find the measure of ∠A if ∠C = 25° and ∠B = 100°
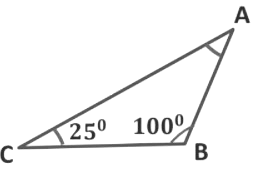
Sol:
We know that the sum of angles of a triangle is 180°
∴ ∠A + ∠B + ∠C = 180°
→ ∠A + 100° + 25° = 180°
→ 125° + ∠A = 180°
→ ∠A = 180° − 125°
→ ∠A = 55°
Hence, the measure of ∠A is 55°
Example: Find the measure of a triangle which are in the ratio of 2:1:1
Sol: Let the common ratio be x°
The measure of given angles of the triangle be 2x°, x°, and x° respectively.
We know that the sum of angles of a triangle is 180°
2x° + x° + x° = 180°
4x° = 180°
x° = 180°/4
x° = 45°
So the measure of the angles ( (2 × 45°), 45°, and 45°) i.e.,90°, 45°and 45°
Example: If the angles of a triangle have measures (3A + 40°),(A + 20°), 2A. Find the value of A.
Sol: Let∆ABC,
∠BAC = (3A + 40°), ∠ACB = (A + 20°), and∠ABC = 2A
We know that the sum of angles of a triangle is 180°
∴ ∠BAC + ∠ACB + ∠ABC = 180°
→ (3A + 40°) + (A + 20°) + 2A = 180°
→ 3A + 40° + A + 20° + 2A = 180°
→ 3A + A + 2A + 40° + 20° = 180°
→ 6A + 60° = 180°
→ 6A + 60° − 60° = 180° − 60°
→ 6A = 120°
→ A = 120/6°
→ A = 20°
Hence, the value of A is 20°
Two Special Triangles: Equilateral And Isosceles
Equilateral Triangle
A triangle in which all three sides are of equal length and three angles are equal. Each angle is 60°.
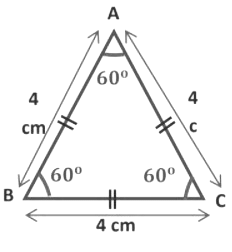
∆ABC is an equilateral triangle in which we see all the three sides of the triangle are of equal length and the measure of all the angles of the triangle is also equal.
Isosceles Triangle:
A triangle in which two sides are of equal length and angles opposite to equal sides are equal.

∆ABC is an isosceles triangle in which we see two sides of the triangle are of equal length and the angles opposite to equal sides are equal.
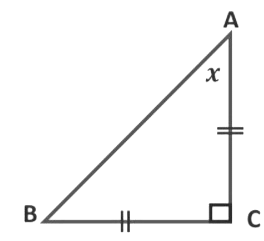
1. Find angle x in the following figure: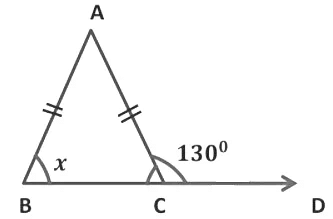
∆ABC is an isosceles triangle.
So, AB = AC
∠ABC = ∠ACB
x = ∠ACB
∠ACB + ∠ACD = 180°... (Linear pair)
x + 130° = 180°
x + 130° − 130° = 180° − 130°
x = 50°
2. Find angle x in the following figure:
Sol: ∆ABC is an isosceles triangle.
So, AB = BC
∠ABC = ∠CAB
∠CAB = x
Hence,
∠ABC = ∠CAB = x∠ABC + ∠BCA + ∠CAB = 180°...(angle sum property)
x + 90° + x = 180°
2x + 90° = 180°
2x + 90° − 90° = 180° − 90°
2x = 90°
x = 90°/2
x = 45°
Sum of the Lengths of Two Sides of a Triangle
In a school, Math’s teacher tells students to draw a triangle. After some time, teacher asked the students, have you drawn the triangle? Students: yes. So, firstly teacher asked Ben, how have you drawn the triangle? And what is the length of sides of the triangle you took to draw the triangle?
Ben said I have drawn a triangle in which I took the length of the sides of the triangle is 5 cm, 7 cm, and 12 cm.
So, the teacher said to students to check if we can draw a triangle from this length of the sides of the triangle.
To check this, “The sum of any two sides of the triangle is greater than the length of the third side.”
So, let’s find out. We have 5 cm, 7 cm, and 12 cm three sides of the triangle. So,
Here, we see the sum of the two sides is equal to third sides.
It means the triangle with sides 5 cm, 7 cm, and 12 cm cannot be formed.
Now, the teacher asked to Nobita, how has she drawn the triangle?
She told that to draw a triangle she took the length of the sides of the triangle is 3 cm, 4 cm, and 5 cm. The teacher said let’s check these sides are correct or not?
According to Nobita, 
Here, we see the sum of the two sides is greater than the third side. Can Nobita draw a triangle from it? No, because this is only one case.
Now, we see the second combination,
Now, we see the third combinations
Here, all three cases can satisfy the condition. It means the triangle with sides 3 cm, 4 cm, and 5 cm can be formed.
Another way we can also find the given sides can form a triangle or not.
If the difference of any two sides of the triangle is less than the third side then we are able to draw a triangle.
Example: Let us consider the sides of the triangle be 5 cm, 10 cm, and 12 cm. So,
Here, we see the difference of the two sides is less than the third side. It means according to the theorem, the triangle can be formed with sides 5 cm, 10 cm, and 12 cm.
Example: Is it possible to have a triangle with the following sides?
(i) 3 cm, 5 cm, and 7 cm
Sol: We know, the sum of two sides of a triangle is greater than the third side.
We check this property for the given sides of the triangle.
Here, we see the sum of two sides of the triangle is greater than the third side. Hence, it follows triangle inequality. It means the triangle with sides 3 cm, 5 cm, and 7 cm can be formed.
Right-Angled Triangles and Pythagoras Theorem
Pythagoras theorem is related to the right-angled triangle. So, let us consider a right-angled triangle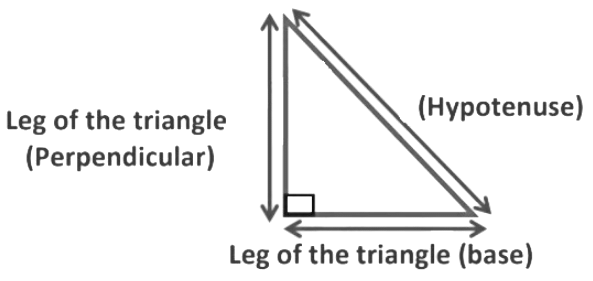
In a right-angled triangle, the side opposite to the right angle is called the hypotenuse, and the other two sides are known as legs of the right-angled triangle. So, perpendicular, base, and hypotenuse are the three sides of the right-angled triangle. Now, according to this theorem, if you have a right-angled triangle in which
a→ Leg of a triangle (Perpendicular side)
b→ Leg of a triangle (Base side)
c→ Hypotenuse
Then let’s try this if we draw a square on the perpendicular side that means each side of the square would be equal to a and the area of that square is equal to a2.
If we draw a square on the base side that means each side of the square would be equal to b and the area of that square is equal to b2.
In the same way, if we draw a square on hypotenuse side that means each side of the square would be equal to c and the area of that square is equal to c2.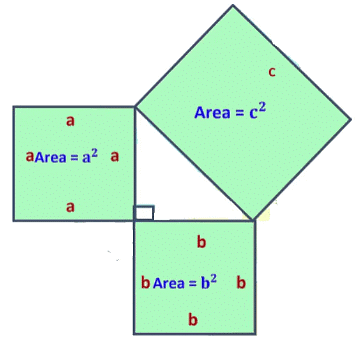 So, according to Pythagoras theorem,
So, according to Pythagoras theorem,
In a right-angled triangle, the square of the hypotenuse equals the sum of the square of its two sides.
∴ (Perpendicular)2 + (Base)2 = (Hypotenuse )2
∴ (a)2 + (b)2 = (c )2
This is called the Pythagoras theorem.

There is another way we prove Pythagoras theorem
Suppose we have eight right angle triangles and two identical squares, and the side of both squares is (a + b).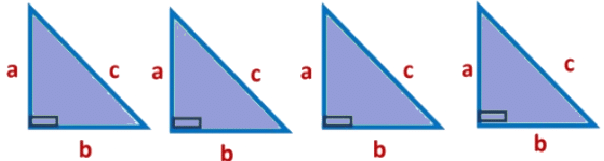
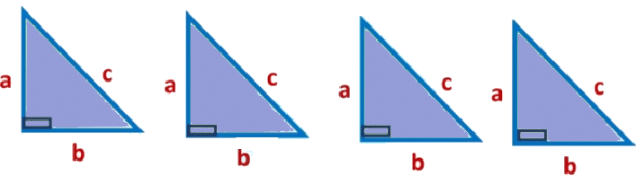
Now, we place four triangles in the first square and remaining four triangles in the second square in a different way as shown below
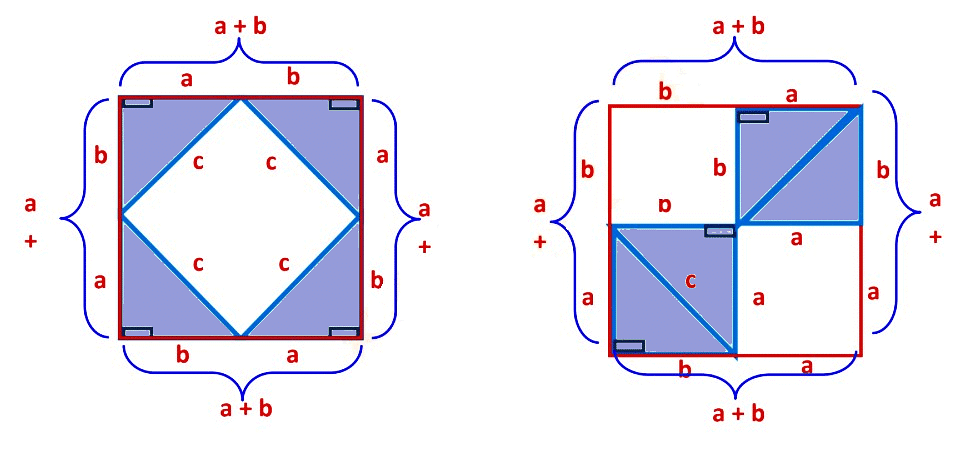
Now, we know the squares are identical and the eight triangles inserted in the squares are also identical.
Uncovered area of 1st square = Uncovered area of 2nd square
Area of inner square of first square = The total area of two uncovered squares in 2nd square
(c )2 = (a)2 + (b)2
Area of a square with side (a + b) = Area of inside square of side c + Area of four inside triangles
Area of a square with side (a + b) = (a + b)2
Area of inside square of side (c) = (c)2
Area of four inside triangles = 4 × Area of one triangle
Area of four inside triangles = 4 × 1/2 × ab = 2ab
(a + b)2 = c2 + 2ab
a2 + b2 + 2ab = c2 + 2ab
a2 + b2 + 2ab − 2ab = c2 + 2ab − 2ab
a2 + b2 = c2
Hence, Pythagoras theorem proved in another way.
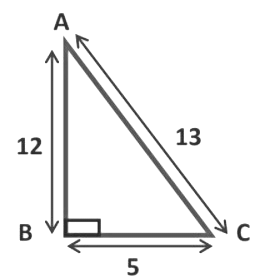
Example 1: Verify Pythagoras theorem in triangle ABC
Sol: In ∆ABC,
AC = 13 (Hypotenuse)
AB = 12 (Perpendicular)
BC = 5 (Base)
By Pythagoras theorem
(AB)2 + (BC)2 = (AC)2
Take LHS: = (AB)2 + (BC)2
= (12)2 + (5)2 = 144 + 25 = 169
Take RHS: = (AC)2S= (13)2 = 169
Here, LHS = RHS
Hence, the Pythagoras theorem is verified for this triangle.
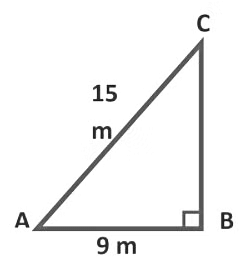
Example 2 : A 15 m long ladder is placed against a wall in such a way that the foot of the ladder is 9 m away from the wall. So, up to what height does the ladder reach the wall?
Sol:
Consider BC be the wall and AC be the ladder.
Then, AB = 9 m and AC = 15 mNow, ∆ABC is a right-angled triangle.
Hence,
(AC)2 = (AB)2 + (BC)2
⇒ (BC)2 = (AC)2 − (AB)2
= (15)2 − (9)2
= 225 − 81 = 144
⇒ BC = √144 = 12 m
Hence, the ladder reaches the wall up to 13 m.
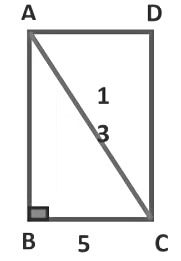
Example 3: Find the perimeter of the rectangle whose length is 5 cm and its diagonal is 13 cm.
Sol: In ∆ABC
(AC)2 = (AB)2 + (BC)2
(13)2 = (AB)2 + (5)2
169 = (AB)2 + 25
169 − 25 = (AB)2 + 25 − 25
144 = (AB)2
(12)2 = (AB)2
12 = AB
Now, we know the perimeter of the rectangle = 2 (l + b)
= 2 (5 + 12)
= 2 (17)
= 34 cm
Hence, the perimeter of the rectangle is 34 cm.
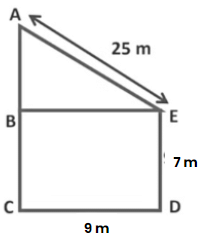
Example 4: A 7 m high pole is 9 m away from a building. If the distance between the top of the pole and top of the building is 25 m then find the height of the building.
Sol: Let AC be the height of the building. ED be the height of the pole. AE be the distance between their tops and CD be the distance between the foot of the pole and
the foot of the building. Now, from E draw EB ⊥ AC
AE = 25 m
BE = CD = 9 m
In the right-angled triangle ∆ABE,(AE)2 = (AB)2 + (BE)2
(25)2 = (AB)2 + (9)2
625 = (AB)2 + 81
Subtracting 81 from both side
625 − 81 = (AB)2 + 81 − 81
576 = (AB)2
∴ AB = 24 m
Since AC = AB + BC and BC = ED = 9 m
∴ AC = 24 + 9 = 33 m
Hence, the height of the building is 33 m.
The converse of Pythagoras theorem
If any triangle obeys the Pythagoras theorem, then the triangle is right-angled.
Let’s explain this theorem by using the example
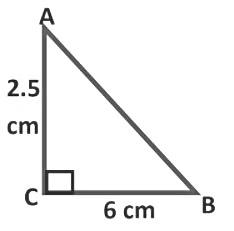
Example 5: Δ ABC is right-angled at C. If AC = 2.5 cm and BC = 6 cm find the length of AB
Sol:
By Pythagoras theorem,
In ∆ABC, (AB)2 = (AC)2 + (BC)2
(AB)2 = (2. 5)2 + (6)2
(AB)2 = 6. 25 + 36
(AB)2 = 42. 25
∴ AB = √42. 25 = 6. 5 cm
Hence, the length of AB is 6. 5 cm
|
77 videos|386 docs|39 tests
|
FAQs on The Triangle and Its Properties Class 7 Notes Maths Chapter 6
| 1. What are the properties of the medians of a triangle? |  |
| 2. How do altitudes of a triangle relate to its area? |  |
| 3. What is the Angle Sum Property of a triangle? |  |
| 4. What are the characteristics of equilateral and isosceles triangles? |  |
| 5. How does the Pythagorean theorem apply to right-angled triangles? |  |