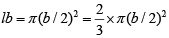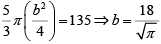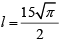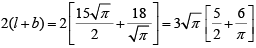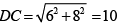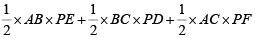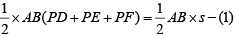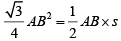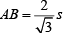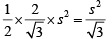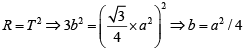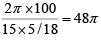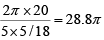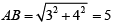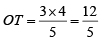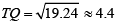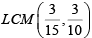CAT 2020: Mensuration | Additional Study Material for CAT PDF Download

Q.1. On a rectangular metal sheet of area 135 sq in, a circle is painted such that the circle touches two opposite sides. If the area of the sheet left unpainted is two-thirds of the painted area then the perimeter of the rectangle in inches is
(a)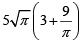 
(b)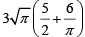
(c)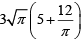 
(d)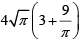

Correct Option is B
Let the length and the breadth of the rectangle be l and b respectively.
As the circle touches the two opposite sides, its diameter will be same as the breadth of the rectangle. Given, lb = 135 and
⇒
From this
∴ Required perimeter:

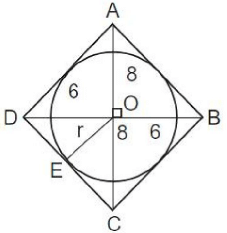
Q.2. A circle is inscribed in a thombus with diagonals 12 cm and 16 cm. The ratio of the area of circle to the area of rhombus is
(a) 5π/18
(b) 6π/25
(c) 3π/25
(d) 2π/15

Correct Option is B

Given the circle is inscribed in the rhombus of diagonals 12 and 16 . Let O be the point of intersection of the diagonals of the rhombus. Then, OE (radius) ⊥ DC.
Also
As area of ΔODC should be the same, we have, 1/2 x 6 x 8 = 6π/25

Q.3. A solid right circular cone of height 27 cm is cut into two pieces along a plane parallel to its base at a height of 18 cm from the base. If the difference in volume of the two pieces is 225 cc, the volume, in cc, of the original cone is
(a) 232
(b) 256
(c) 264
(d) 243 

Correct Option is D
As the cone is cut at one-third height from the top (the vertex), the total volume is proportional to the cubes of the heights of the two parts.
Ratio of volumes two parts =   = 1 : 27
Hence the bottom part will have volume of 27 - 1 i.e., 26 parts.
Given ( 26 - 1) i.e., 25 parts -225 cc.
Hence the required answer is 27 parts = 27 x 255 / 25 = 243 cc. 

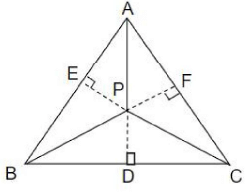
Q.4. From an interior point of an equilateral triangle, perpendiculars are drawn on all three sides. The sum of the lengths of the three perpendiculars is s. Then the area of the triangle is
(a)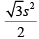 
(b)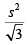 
(c)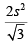 
(d)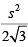 

Correct Option is B

PD + PE + PF = s
Area of =
As AB = BC = CA, we've
=
Now
⇒
Required Value =

Q.5. The sum of the perimeters of an equilateral triangle and a rectangle is 90 cm. The area, T, of the triangle and the area, R, of the rectangle, both in sq cm, satisfy the relationship R = T² . If the sides of the rectangle are in the ratio 1: 3, then the length, in cm, of the longer side of the rectangle, is  
(a) 24
(b) 27
(c) 21
(d) 18 

Correct Option is B
Let the breadth of the rectangle be b.
Length of the rectangle = 3b
Let a be the side of the equilateral triangle.
Given,

Given,
2(4b) + 3a = 90
⇒ 8 (a² / 4) + 3a - 90 = 0
⇒ 2a² + 3a - 90 = 0
⇒ (a - 6)(2a + 15) = 0
⇒ a = 6
∴ b = 9 ⇒ 3b = 27

Q.6. Two circular tracks T1 and T2 of radii 100 m and 20 m, respectively touch at a point A. Starting from A at the same time, Ram and Rahim are walking on track T1 and track T2 at speeds 15 km/hr and 5 km/hr respectively. The number of full rounds that Ram will make before he meets Rahim again for the first time is
(a) 4
(b) 3
(c) 2
(d) 5 

Correct Option is B
Time taken by each of them to complete one round
= Circumference of the circle / speed
Time taken for Ram to cover one round =
Time taken for Rahim to cover one round =
Time taken by Ram and Rahim meet each other for the first time = LCM of 48π and 28.8π = 144π
∴ Number of rounds made by Ram before he meets Rahim for the first time = 144π / 48π
= 3

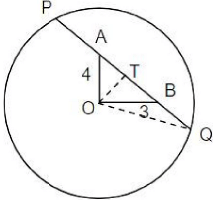
Q.7. Let C be a circle of radius 5 meters having center at O. Let PQ be a chord of C that passes through points A and B where A is located 4 meters north of O and B is located 3 meters east of O. Then, the length of PQ, in meters, is nearest to 
(a) 7.2
(b) 7.8
(c) 6.6
(d) 8.8 

Correct Option is D



OT = 2.4M
In ΔOTQ
OQ² = OT² + TQ² ⇒ TQ² = OQ² - OT²
= (5)² - (2.4)²
= 19.24
⇒
∴ PQ = 2TQ = 8.8m

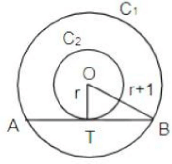
Q.8. Let C1 and C2 be concentric circles such that the diameter of C1 is 2 cm longer than that of C2. If a chord of C1 has length 6 cm and is a tangent to C2, then the diameter, in cm, of C1 is 

Ans: 10

Given, d + 2 = D ⇒ r + 1 = R
In the figure OT = r and OB = r + 1
OT ⊥  AB as AB is the tangent
OT bisects AB i.e., TB = 6/2 = 3
Now, in ΔOTB, OT² + TB² = OB² 
∴ r² + 3² = (r + 1)² ⇒ r = 4
∴ D = 2(R ) = 2(r + 1) = 10cm

Q.9. Anil, Sunil, and Ravi run along a circular path of length 3 km, starting from the same point at the same time, and going in the clockwise direction. If they run at speeds of 15 km/hr, 10 km/hr, and 8 km/hr, respectively, how much distance in km will Ravi have run when Anil and Sunil meet again for the first time at the starting point?
(a) 4.2
(b) 5.2
(c) 4.8
(d) 4.6

Correct Option is C
Time taken by Anil and Sunil meet at the starting point
= 3/5
Distance run by Ravi in 3 / 5 hours = (3 / 5) x  8 = 24 / 5 = 4.8 km

Q.10. In a trapezium ABCD, AB is parallel to DC, BC is perpendicular to DC and ∠BAD = 45° . If DC = 5 cm , BC= 4 cm, the area of the trapezium in sq cm is

Ans: 28
Dropping a perpendicular DE onto AB, the figure is divided into two parts - a rectangle of dimensions 4 x 5 and an isosceles triangle AED.
Required answer = Area of rectangle + Area of triangle = 4 x 5 + 1/2(4 x4) = 28cm²