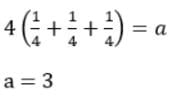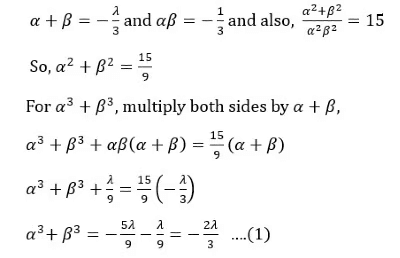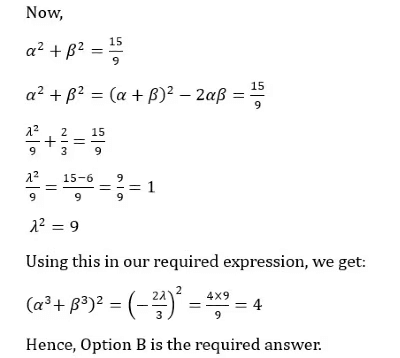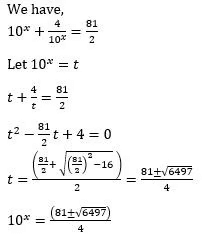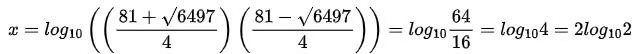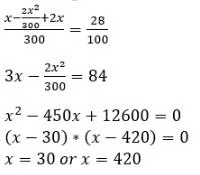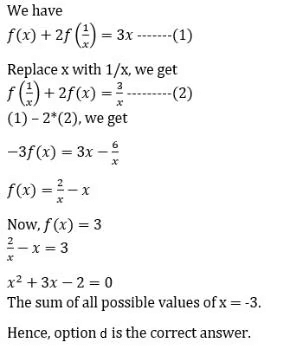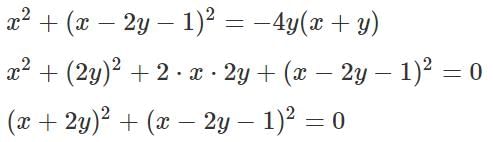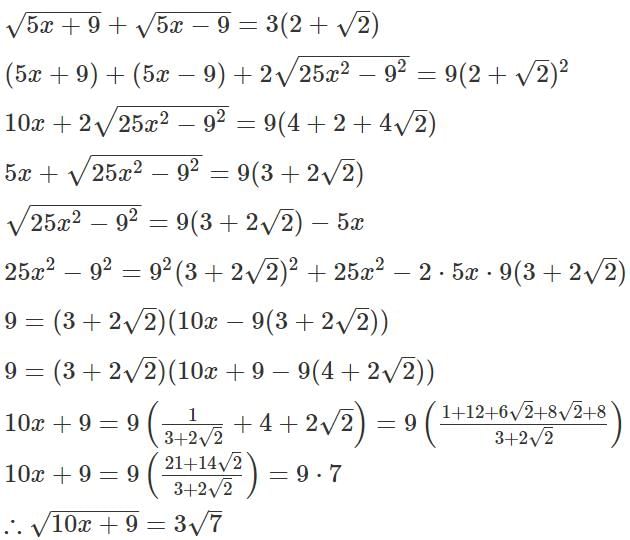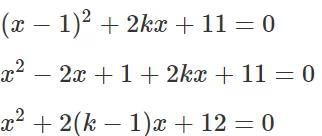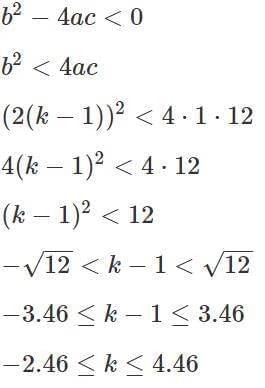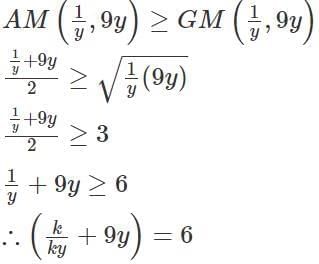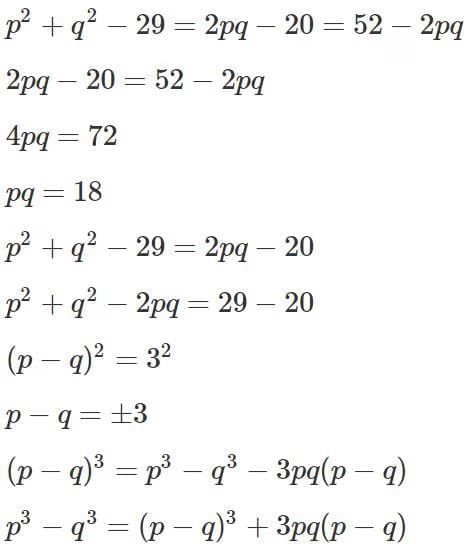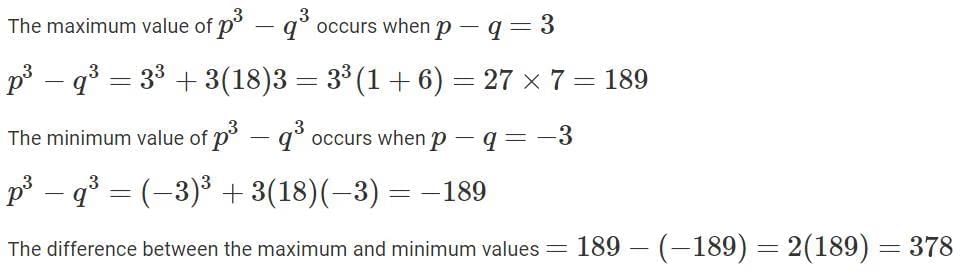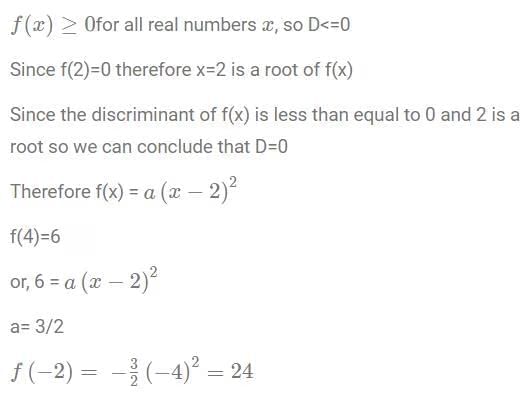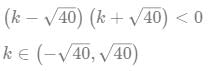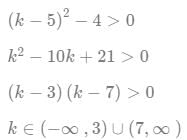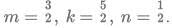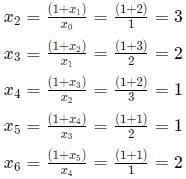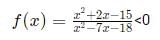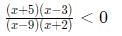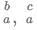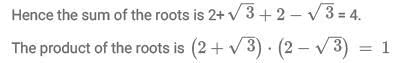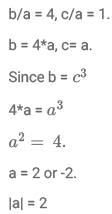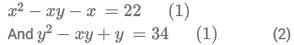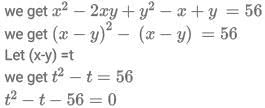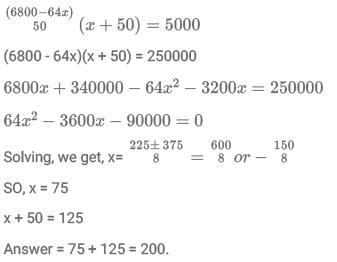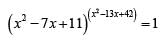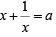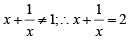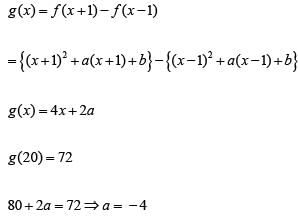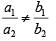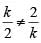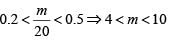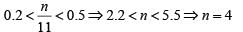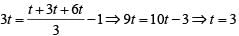Linear Equations CAT Previous Year Questions with Answer PDF
2024
Q1: Let x, y, and z be real numbers satisfying
4(x2 + y2 + z2) = a,
4(x - y - z) = 3 + a
Then a equals
(a) 1
(b) 4
(c) 3
(d) 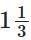
Ans: c
Sol: Given,
4(x² + y² + z²) = a ... (i)
4(x - y - z) = 3 + a ... (ii)
(i) - (ii)
4x² + 4y² + 4z² - 4x + 4y + 4z + 3 = 0
(2x - 1)² + (2y + 1)² + (2z + 1)² = 0
x = 1/2, y = -1/2, z = -1/2
Putting these values in (i), we get
Q2: A shop wants to sell a certain quantity (in kg) of grains. It sells half the quantity and an additional 3 kg of these grains to the first customer. Then, it sells half of the remaining quantity and an additional 3 kg of these grains to the second customer. Finally, when the shop sells half of the remaining quantity and an additional 3 kg of these grains to the third customer, there are no grains left. The initial quantity, in kg, of grains is
(a) 50
(b) 18
(c) 36
(d) 42
Ans: d
Sol: Let the quantity of grain left before giving to the third customer be z kg.
So,
z/2 + 3 = z
z = 6 kg
Let the quantity of grain left before giving to the second customer be y kg.
So,
y/2 - 3 = 6
y = 18 kg
Similarly, let the quantity of grain left before giving to the first customer be x kg.
So,
x/2 - 3 = 18
x = 42 kg
Q3: If x and y satisfy the equations |x| + x + y = 15 and x + |y| - y = 20, then (x - y) equals
(a) 15
(b) 10
(c) 20
(d) 5
Ans: (a)
Sol:
Case1. When x ≥ 0 and y ≥ 0,
2x + y = 15 and, x + y – y = 20
On solving, we get,
X = 20 and y = –25 which is not possible.
Case2. When x ≥ 0 and y < 0,
2x + y = 15 and, x – 2y = 20
On solving, we get,
X = 10 and y = –5 [which is possible].
Case3. When x < 0 and y ≥ 0
–x + x + y = 15 and x + y – y = –20
On solving, we get, x = –20 and y = 15 which is not possible.
Case4. When x < 0 and y < 0,
–x + x + y = 15 and x – y – y = 20
On solving, we get x = 50 and y = 15 which is not possible.
So, from the case1, case2, case3 and case4.
The possible value of x and y is 10 and –5 respectively.
So, the value of (x – y) = (10 – (–5)) = 15
Q4: The roots of α, β of the equation 3x2 + λx - 1 = 0, satisfy 1/α2 + 1/β2 = 15.
The value of (α3 + β3)2, is
(a) 1
(b) 4
(c) 9
(d) 16
Ans: b
Sol:
Q5: If x and y are real numbers such that 4x2 + 4y2 - 4xy - 6y + 3 = 0, then the value of (4x + 5y) is
Ans: 7
Sol: Given,
4x2 + 4y2 – 4xy – 6y + 3 = 0
The above can be written as,
(2x – y)2 + 3(y – 1)2 = 0
Giving, y = 1 and x = ½
So, the value of (4x + 5y) = (4 × ½ + 5 × 1) = 7
Hence, 7 is the required answer.
Q6: The sum of all distinct real values of x that satisfy the equation 10x + 4/10x = 81/2, is
(a) 3log102
(b) 2log102
(c) 4log102
(d) log102
Ans: b
Sol:
Therefore, the sum of distinct values of x
Hence, option B is the correct answer.
Q7: A certain amount of water was poured into a 300 litre container and the remaining portion of the container was filled with milk. Then an amount of this solution was taken out from the container which was twice the volume of water that was earlier poured into it, and water was poured to refill the container again. If the resulting solution contains 72% milk, then the amount of water, in litres, that was initially poured into the container was
Ans: 30
Sol: Let the amount of the water initially poured be x liters.
Therefore, the amount of milk = (300 – x) liters.
According to Question,But x cannot be 420 as the capacity of the vessel is 300L.
Hence, x = 30 L.
Q8: For any non-zero real number x, let f(x) + 2f(1/x) = 3x. Then, the sum of all possible values of x for which f(x) = 3, is
(a) 3
(b) -2
(c) 2
(d) -3
Ans: d
Sol:
Q9: For some constant real numbers p, k and a, consider the following system of linear equations in x and y:
px - 4y = 2
3x + ky = a
A necessary condition for the system to have no solution for (x, y), is
(a) 2a + k ≠ 0
(b) ap + 6 = 0
(c) kp + 12 ≠ 0
(d) ap - 6 = 0
Ans: a
Sol: For the system of equations to have no solution, the lines represented by the equation must be parallel but not coincident.
px – 4y = 2 …(1)
3x + ky = a …(2)
For the equation to follow the condition
p / 3 = –4 / k
pk = –12 …(3)
Also, 2 / a ≠ –4 / k => 2a + k ≠ 0
Hence, option 1 is the correct answer.
2023
Q1: If x and y are real numbers such that x2 + (x − 2y − 1)2 = −4y(x + y), then the value x−2y is [2023]
(a) 0
(b) 1
(c) 2
(d) -1
Ans: b
Sol:
Since x & y are real numbers, (x + 2y) & (x − 2y − 1) are both real.
A square of a real number is always non-negative.
For this reason, for the equation: (x + 2y)2 + (x − 2y − 1)2 = 0 to be true, both (x + 2y) & (x − 2y − 1) must be equal to 0.
x − 2y − 1 = 0
x − 2y = 1
We solve the linear equations (x + 2y = 0) & (x − 2y − 1 = 0) to get the exact values of x & y, but that is not required to solve the question at hand.
Q2: If 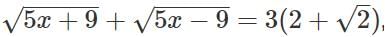 then
then 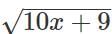 is equal to [2023]
is equal to [2023]
(a) 4√5
(b) 2√7
(c) 3√31
(d) 3√7
Ans: d
Sol:
Q3: The number of integer solutions of equation 2 |x| (x2 + 1)= 5x2 is [2023]
Ans: 3
Sol: 2 |x| (x2 + 1)= 5x2
Let |x| = k
2k (k2 + 1) = 5k2
Either k = 0; or 2(k2 + 1) = 5k
2k2 – 5k + 2 = 0
2k2 – 4k – k + 2 = 0
2k(k – 2) –1(k – 2) = 0
(2k – 1)(k – 2) = 0
k = 0.5 or k = 2
Therefore, k which is |x|, can take the values 0, 0.5 or 2
So, x can take the values 0, -0.5, 0.5, -2, 2
Since we are looking for integral solutions, x can only take the values 0, 0.5 or 2
Therefore, there are only 3 integral solutions to 2 |x| (x2 + 1) = 5x2.
Q4: Let α & and β be the two distinct roots of the equation 2x2 - 6x + k = 0, such that (α + β) and αβ are the distinct roots of the equation x2 + px + p = 0. Then, the value of 8(k - p) is [2023]
Ans: 6
Sol:
Q5: The equation x3 + (2r + 1)x2 + (4r - 1)x + 2 = 0 has -2 as one of the roots. If the other two roots are real, then the minimum possible non-negative integer value of r is [2023]
Ans: 2
Sol:
Q6: The sum of all possible values of x satisfying the equation 24x2 - 22x2 + x + 16 + 22x + 30 = 0, is [2023]
(a) 3/2
(b) 5/2
(c) 1/2
(d) 3
Ans: c
Sol:
Q7: Let k be the largest integer such that the equation (x−1)2 + 2kx + 11 = 0 has no real roots. If y is a positive real number, then the least possible value of k/4y + 9y is
Ans: 6
Sol:Since the equation above has no real roots, the discriminant of the equation should be negative.
The largest integral value that k can take is 4.
Now, we need to minimize k/4y + 9y where k takes the largest integral value and y is positive…1/y & 9y are both positive real numbers, therefore, their A.M is greater than equal to their G.M.
Q8: If p2 + q2 − 29 = 2pq − 20 = 52 − 2pq, then the difference between the maximum and minimum possible value of (p3 − q3) is
(a) 486
(b) 189
(c) 378
(d) 243
Ans: c
Sol:
2022
Q1: Let a, b, c be non-zero real numbers such that b2 < 4ac, and f(x) = ax2 + bx + c. If the set S consists of all integers m such that f(m) < 0, then the set S must necessarily be
(a) the empty set
(b) the set of all positive integers
(c) the set of all integers
(d) either the empty set or the set of all integers
Ans: d
Sol: b2 < 4ac means that the discriminant is less than 0. Therefore, f(x) > 0 for all x if the coefficient of x2 is positive, and f(x)<0 for all x if the coefficient of x2 is negative.
We are given that f(m)<0 and m is an integer.
So the set containing values of m will either be empty if the coefficient of x2 is positive, or it will be a set of all integers if the coefficient of x2 is negative.
Q2: In an election, there were four candidates and 80% of the registered voters casted their votes. One of the candidates received 30% of the casted votes while the other three candidates received the remaining casted votes in the proportion 1 : 2 : 3. If the winner of the election received 2512 votes more than the candidate with the second highest votes, then the number of registered voters was
(a) 50240
(b) 62800
(c) 60288
(d) 40192
Ans: b
Sol:
Let there be total 100x registered voters. 80x casted their votes.
One candidate got 30% of 80x = 24x votes.
The remaining got 56x total votes in the ratio 1:2:3, i.e., the winner got (3/6)56x = 28x votes. And the second highest votes were 24x.
4x = 2512
So, 100x = 62800
Q3: In an examination, there were 75 questions. 3 marks were awarded for each correct answer, 1 mark was deducted for each wrong answer and 1 mark was awarded for each unattempted question. Rayan scored a total of 97 marks in the examination. If the number of unattempted questions was higher than the number of attempted questions, then the maximum number of correct answers that Rayan could have given in the examination is
(a) 22
(b) 23
(c) 24
(d) 25
Ans: c
Sol:
Let the number of correct, wrong, and unattempted questions be a, b and c respectively.
a + b + c = 75 ….(i)
3a – b + c = 97 ….(ii)
(ii) – (i)
=> a – b = 11 ……(iii)
c > a + b
We have to find the max value of a. For that, a + b should be max
=> c = 38 and a + b = 37 …….(iv)
(iii) + (iv)
=> a = 24
Q4: Let r and c be real numbers. If r and –r are roots of 5x3 + cx2 – 10x + 9 = 0, then c equals
(a) -(9/2)
(b) 4
(c) -4
(d) 9/2
Ans: a
Sol:
Q5: Let f(x) be a quadratic polynomial in x such that f(x) ≥ 0 for all real numbers x. If f(2) = 0 and f(4) = 6, then f(–2) is equal to
(a) 36
(b) 12
(c) 6
(d) 24
Ans: d
Sol:
Hence option D.
Q6: If 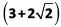 is a root of the equation ax2 + bx + c = 0, and
is a root of the equation ax2 + bx + c = 0, and 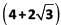 is a root of the equation ay2 + my + n = 0, where a, b, c, m and n are integers, then the value of
is a root of the equation ay2 + my + n = 0, where a, b, c, m and n are integers, then the value of 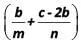 is
is
(a) 4
(b) 0
(c) 1
(d) 3
Ans: a
Sol:
a, b, c, m and n are integers so if one root is 3 + 2 √2 then the other root is 3 − 2√2
Sum of roots = 6 = -b/a or b= -6a
Product of roots = 1 = c/a or c = a
a, b, c, m and n are integers so if one root is 4 + 2√3 then the other root is 4 − 2√3
Sum of roots = 8 = -m/a or m = -8a
product of roots = 4 = n/a or n = 4a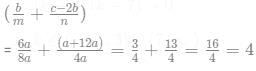
Q7: Suppose k it is any integer such that the equation 2x2 + kx + 5 = 0 has no real roots and the equation x2 + (k − 5)x + 1 = 0 has two distinct real roots for x. Then, the number of possible values of k is
(a) 9
(b) 13
(c) 8
(d) 7
Ans: a
Sol:
2x2 + kx + 5 = 0 has no real roots so D < 0
k2 − 40 < 0
has two distinct real roots so D > 0
Therefore possibe value of k are -6, -5, -4, -3, -2, -1, 0, 1, 2 In 9 total 9 integer values of k are possible....
2021
Q1: Amar, Akbar and Anthony are working on a project. Working together Amar and Akbar can complete the project in 1 year, Akbar and Anthony can complete in 16 months, Anthony and Amar can complete in 2 years. If the person who is neither the fastest nor the slowest works alone, the time in months he will take to complete the project is
Ans: 32
Sol: Let the total work be 48 units. Let Amar do 'm' work, Akbar do 'k' work, and Anthony do 'n' units of work in a month.
Amar and Akbar complete the project in 12 months. Hence, in a month they do 48/12 = 4units of work.
m+k = 4.
Similarly, k+n = 3, and m+n = 2.
Solving the three equations, we getHere, Amar works neither the fastest not the slowest, and he does 1.5 units of work in a month.
Hence, to complete the work, he would take 48/1.5 = 32 months.
Q2: Amal purchases some pens at ₹ 8 each. To sell these, he hires an employee at a fixed wage. He sells 100 of these pens at ₹ 12 each. If the remaining pens are sold at ₹ 11 each, then he makes a net profit of ₹ 300, while he makes a net loss of ₹ 300 if the remaining pens are sold at ₹ 9 each. The wage of the employee, in INR, is [2021]
Ans: 1000
Sol: Let the number of pens purchased be n. Then the cost price is 8n. The total expenses incurred would be 8n + W, where W refers to the wage.
Then SP in the first case =12 × 100 + 11 × (n−100)
Given profit is 300 in this case: 1200 + 11n - 1100 - 8n - W = 300 ⇒ 3n - W = 200
In second case: 1200 + 9n - 900 - 8n - W = -300 (Loss). ⇒ W-n = 600.
Adding the two equations: 2n = 800
n = 400.
Thus W = 600 + 400 = 1000
Q3: A basket of 2 apples, 4 oranges and 6 mangoes costs the same as a basket of 1 apple, 4 oranges and 8 mangoes, or a basket of 8 oranges and 7 mangoes. Then the number of mangoes in a basket of mangoes that has the same cost as the other baskets is [2021]
(a) 11
(b) 13
(c) 10
(d) 12
Ans: b
Sol: Let the cost of an apple, an orange and a mango be a, o, and m respectively.
Then it is given that:
2a + 4o + 6m = a + 4o + 8m
or a = 2m.
Also, a + 4o + 8m = 8o + 7m
10m - 7m = 4o
3m = 4o.
We can now express the cost of a basket in terms of mangoes only:
2a + 4o + 6m = 4m + 3m + 6m = 13m.
Q4: Onion is sold for 5 consecutive months at the rate of Rs 10, 20, 25, 25, and 50 per kg, respectively. A family spends a fixed amount of money on onion for each of the first three months, and then spends half that amount on onion for each of the next two months. The average expense for onion, in rupees per kg, for the family over these 5 months is closest to [2021]
(a) 26
(b) 18
(c) 16
(d) 20
Ans: b
Sol: Let us assume the family spends Rs. 100 each month for the first 3 months and then spends Rs. 50 in each of the next two months.
Then amount of onions bought = 10, 5, 4, 2, 1, for months 1-5 respectively.
Total amount bought = 22kg.
Total amount spent = 100 + 100 + 100 + 50 + 50 = 400.
Average expense = 400/22 = Rs.18.18 ≈ 18
Q5: The amount Neeta and Geeta together earn in a day equals what Sita alone earns in 6 days. The amount Sita and Neeta together earn in a day equals what Geeta alone earns in 2 days. The ratio of the daily earnings of the one who earns the most to that of the one who earns the least is [2021]
(a) 3.2
(b) 11.7
(c) 11.3
(d) 7.3
Ans: c
Sol: Let the amounts Neeta, Geeta, and Sita earn in a day be n, g, and s respectively.
Then, it has been given that:
n + g = 6s - i
s + n = 2g - ii
ii-i, we get: s - g = 2g - 6s
7s = 3g.
Let g be 7a. Then s earns 3a.
Then n earns 6s - g = 18a - 7a = 11a.
Thus, the ratio is 11a:3a = 11:3
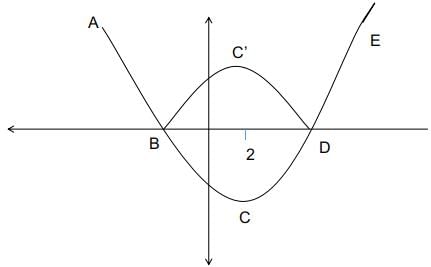
Q6: If r is a constant such that ∣x2 − 4x − 13∣ = r has exactly three distinct real roots, then the value of r is [2021]
(a) 17
(b) 21
(c) 15
(d) 18
Ans: a
Sol:
The quadratic equation of the form ∣x2 − 4x − 13∣ = r has its minimum value at x = -b/2a, and hence does not vary irrespective of the value of x.
Hence at x = 2 the quadratic equation has its minimum.
Considering the quadratic part : ∣x2 − 4x − 13∣ . as per the given condition, this must-have 3 real roots.
The curve ABCDE represents the function ∣x2 − 4x − 13∣. Because of the modulus function, the representation of the quadratic equation becomes :
ABC'DE.
There must exist a value, r such that there must exactly be 3 roots for the function. If r = 0 there will only be 2 roots, similarly for other values there will either be 2 or 4 roots unless at the point C'.
The point C' is a reflection of C about the x-axis. r is the y coordinate of the point C' :
The point C which is the value of the function at x = 2, = 22 − 8 − 13 = -17,
the reflection about the x-axis is 17.
Q7: If x0 = 1, x1 = 2 , and 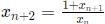 n=0,1,2,3,......, then x2021 is equal to [2021]
n=0,1,2,3,......, then x2021 is equal to [2021]
(a) 4
(b) 1
(c) 3
(d) 2
Ans: d
Sol: x0 = 1, x1 = 2
Hence, the series begins to repeat itself after every 5 terms. Terms whose number is of the form 5n are 1, 5n+1 are 2... and so on, where n=0,1,2,3,....
2021 is of the form 5n+1. Hence, its value will be 2.
Q8: 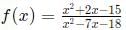 is negative if and only if
is negative if and only if
(a) -5 < x < -2 or 3 < x < 9
(b) x < -5 or -2 < x < 3
(c) -2 < x < 3 or x > 9
(d) x < -5 or 3 < x < 9
Ans: a
Sol:
We have four inflection points -5, -2, 3, and 9.
For x < -5, all four terms (x + 5), (x - 3), (x - 9), (x + 2) will be negative. Hence, the overall expression will be positive. Similarly, when x > 9, all four terms will be positive.
When x belongs to (-2, 3), two terms are negative and two are positive. Hence, the overall expression is positive again.
We are left with the range (-5, -2) and (3, 9) where the expression will be negative.
Q9: Suppose one of the roots of the equation 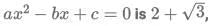 Where a,b and c are rational numbers and
Where a,b and c are rational numbers and 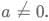 If
If 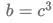 then |a| equals.
then |a| equals.
(a) 1
(b) 2
(c) 3
(d) 4
Ans: b
Sol: Given a, b, c are rational numbers.
Hence a, b, c are three numbers that can be written in the form of p/q.
Hence if one both the root isand considering the other root to be x.The sum of the roots and the product of the two roots must be rational numbers.
For this to happen the other root must be the conjugate ofso the product and the sum of the roots are rational numbers which are represented by:
Q10: Consider the pair of equations: 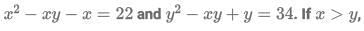 If x > y, then x - y equals
If x > y, then x - y equals
(a) 6
(b) 4
(c) 7
(d) 8
Ans: d
Sol: We have :
Adding (1) and (2)
(t-8)(t+7) =0
so t = 8
so x-y = 8
Q11: A shop owner bought a total of 64 shirts from a wholesale market that came in two sizes, small and large. The price of a small shirt was INR 50 less than that of a large shirt. She paid a total of INR 5000 for the large shirts, and a total of INR 1800 for the small shirts. Then, the price of a large shirt and a small shirt together, in INR, is
(a) 175
(b) 150
(c) 200
(d) 225
Ans: c
Sol: Let the number of large shirts be l and the number of small shirts be s.
Let the price of a small shirt be x and that of a large shirt be x + 50.
Now, s + l = 64
l (x+50) = 5000
sx = 1800
Adding them, we get,
lx + sx + 50l = 6800
64x +50l = 6800
Substituting l = (6800 - 64x) / 50, in the original equation, we getAlternate approach: By options.
Hint: Each option gives the sum of the costs of one large and one small shirt. We know that large = small + 50
Hence, small + small + 50 = option.
SMALL = (Option - 50)/2
LARGE = Small + 50 = (Option + 50)/2
Option A and Option D gives us decimal values for SMALL and LARGE, hence we will consider them later.
Lets start with Option B .
Large = 150 + 50 / 2 = 100
Small = 150 - 50 / 2 = 50
Now, total shirts = 5000/100 + 1800/50 = 50 + 36 = 86 ( X - This is wrong)
Option C -
Large = 200 + 50 / 2 = 125
Small = 200 - 50 / 2 = 75
Total shirts = 5000/125 + 1800/75 = 40 + 24 = 64 ( This is the right answer)
Q12: If 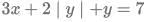 and
and 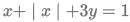 then
then 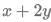 is:
is:
(a) -(4/3)
(b) 8/3
(c) 0
(d) 1
Ans: c
Sol: We need to check for all regions:
x >= 0, y >= 0
x >= 0, y < 0
x < 0, y >= 0
x < 0, y < 0
However, once we find out the answer for any one of the regions, we do not need to calculate for other regions since the options suggest that there will be a single answer.
Let us start with x >= 0, y >= 0,
3x + 3y = 7
2x + 3y = 1
Hence, x = 6 and y = -11/3
Since y > = 0, this is not satisfying the set of rules.
Next, let us test x >= 0, y < 0,
3x - y = 7
2x + 3y = 1
Hence, y = -1 x = 2.
This satisfies both the conditions.
Hence, this is the correct point.
WE need the value of x + 2y
x + 2y = 2 + 2(-1) = 2 - 2 = 0.
2020
Q1: If f (5 + x) = f (5 - x) for every real x, and f(x) = 0 has four distinct real roots, then the sum of these roots is [2020]
(a) 0
(b) 40
(c) 10
(d) 20
Ans: d
Sol: Given f (5 + x ) = f (5 - x )
Put x = x - 5
f ( x) = f (10 - x)
∴ Let a, b be two roots of f(x) = 0, then 10 - a,10 - b are also roots of f ( x ) = 0
∴ Hence sum of the roots = a + b + 10 - a + 10 - b = 20
Q2: How many distinct positive integer-valued solutions exist to the equation 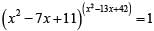 ? [2020]
? [2020]
(a) 6
(b) 8
(c) 2
(d) 4
Ans: a
Sol:
We know if ab = 1
⇒ a = 1 and b is any number
or a = - 1 and b is even
a > 0 and b is 0
case 1: x2 - 13x + 42 = 0 ⇒ x = 6, 7
case 2 : x2 - 7x +11 = 1 ⇒ x2 - 7x +10 = 0 ⇒ x = 2 or 5
case 3: x2 - 7x +11 = -1⇒ x2 - 7x +12 = 0
⇒ x = 4 or 3
Hence number of solutions are 6
Q3: The number of distinct real roots of the equation 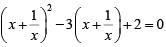 equals [2020]
equals [2020]
Ans: 1
Sol:
Let,
The given equation becomes,
since x is real,
∴ The number of solutions = 1
Q4: Let f ( x) = x2 + ax + b and g ( x) = f ( x + 1) - f ( x - 1) . If f ( x) ≥ 0 for all real x, and g (20) = 72 , then the smallest possible value of b is [2020]
(a) 1
(b) 16
(c) 0
(d) 4
Ans: d
Sol: f ( x) = x2 + ax + b
∴ f (x) = x2 - 4x + b f (x) = (x - 2)2 + b - 4 when b ≥ 4 f ( x) ≥ 0 for all x
∴ The minimum value of b is 4
Q5: Let k be a constant. The equations kx + y = 3 and 4x + ky = 4 have a unique solution if and only if [2020]
(a) |k| ≠ 2
(b) |k| = 2
(c) k ≠ 2
(d) k = 2
Ans: a
Sol: Simultaneous equation have a unique solution only if
From the given equations, a unique solution would exist only if
⇒ k 2 ≠ 4 ⇒| k | ≠ 2
Q6: Let m and n be natural numbers such that n is even and 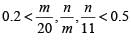 . Then m - 2n equals [2020]
. Then m - 2n equals [2020]
(a) 3
(b) 4
(c) 1
(d) 2
Ans: c
Sol: Given,
since
m - 2n = 9 - 2 x 4 =1
Q7: Dick is thrice as old as Tom and Harry is twice as old as Dick. If Dick's age is 1 year less than the average age of all three, then Harry's age, in years, is [2020]
Ans: 18
Sol: Let the age of Tom be t.
Ages of Dick and Harry are 3t and 6t respectively
Given,
Age of Harry = 6 x 3 = 18
Q8: In the final examination, Bishnu scored 52% and Asha scored 64%. The marks obtained by Bishnu is 23 less, and that by Asha is 34 more than the marks obtained by Ramesh. The marks obtained by Geeta, who scored 84%, is [2020]
(a) 439
(b) 399
(c) 357
(d) 417
Ans: b
Sol: Let the total marks be T and scores of Bishnu, Asha and Ramesh be a, b and c respectively.
Given, a = 52% of T = c - 23 and b = 64% of T = c + 34
Hence, (64 - 52)% of T = (c + 34) - (c - 23) = 57
i.e. 12% of T = 57
Hence, score of Geeta = 84% of T = 7 ´ 57 = 399
|
167 videos|229 docs|95 tests
|
FAQs on Linear Equations CAT Previous Year Questions with Answer PDF
| 1. What are linear and quadratic equations? |  |
| 2. How do you solve a linear equation? |  |
| 3. How do you solve a quadratic equation? |  |
| 4. What are the applications of linear and quadratic equations? |  |
| 5. Can linear and quadratic equations have multiple solutions? |  |