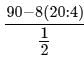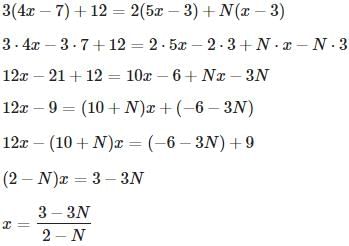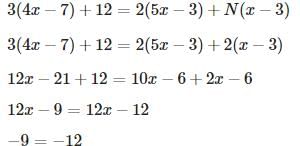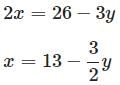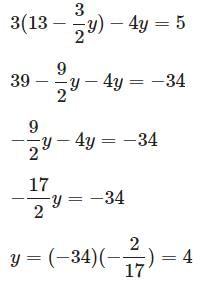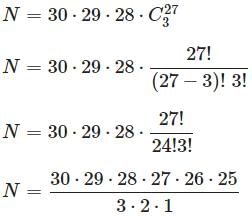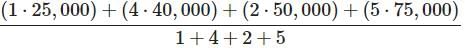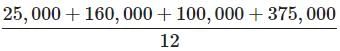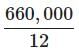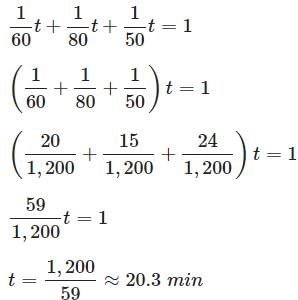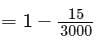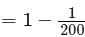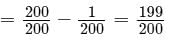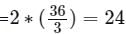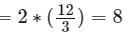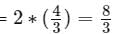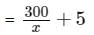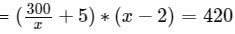Question for Quantitative Practice Questions - 3
Try yourself:A sequence is formed the same way the Fibonacci sequence is formed. Its third and fourth terms are 16 and 30, respectively. What is its first term?
Explanation
A Fibonacci-style sequence starts with two numbers, with each successive number being the sum of the previous two. The second term is therefore the difference of the fourth and third terms, and the first term is the difference of the third and second.
Second term: 30 − 16 = 14
First term: 16 − 14 = 2
Report a problem
Question for Quantitative Practice Questions - 3
Try yourself:Let A be the set of all of the multiples of 3 between 29 and 50. How many subsets of A can be formed?
Explanation
The multiples of 3 between 29 and 50 are 30, 33, 36, 39, 42, 45, and 48 - therefore, A has seven elements total.
The number of subsets in a set can be calculated by raising 2 to the power of the number of elements. Therefore, the answer to our question is 27 = 128 .
Report a problem
Question for Quantitative Practice Questions - 3
Try yourself:For what value of N would the following equation have no solution
3(4x − 7) + 12 = 2(5x − 3) + N(x − 3)
Explanation
Simplify both sides of the equation as much as possible, and solve for x in the equation in terms of N :
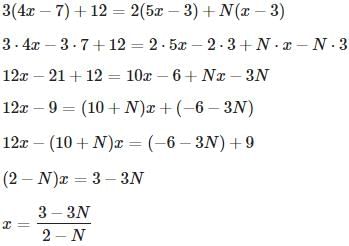
x has exactly one solution unless the denominator is 0 - that is, N = 2 . We make sure that this value renders no solution by substituting:
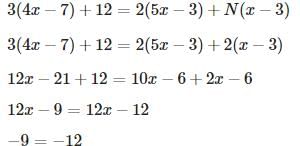
The equation has no solution, and N = 2 is the correct answer.
Report a problem
Question for Quantitative Practice Questions - 3
Try yourself:Solve:
2x + 3y = 26
3x − 4y = 5
Explanation
Solve for x in the first equation:
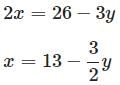
Substitute into the second equation:
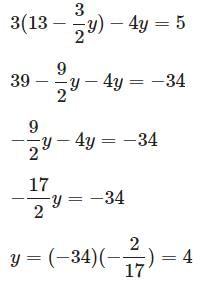
Solve for x .
2x + 3(4) = 26
2x + 12 = 26
2x = 14
x = 7
Report a problem
Question for Quantitative Practice Questions - 3
Try yourself:How many ways can a president, a vice-president, a secretary-treasurer, and three Student Senate representatives be selected from a class of thirty people? You may assume these will be six different people.
Explanation
This can be seen, without loss of generality, as choosing each officer in turn.
There are 30 ways of choosing the president; there are then 29 ways of choosing the vice-president, and 28 ways of choosing the secretary-treasurer. Then 3 Student Senate representatives are chosen from the remaining 27 students; this is a combination of 3 elements from 27 - that is, C327 . By the multiplication principle, the number of possible selections of the officers is:
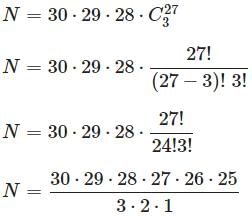
N = 71,253,000
Report a problem
Question for Quantitative Practice Questions - 3
Try yourself:Salaries for employees at ABC Company: 1 employee makes $25,000 per year, 4 employees make $40,000 per year, 2 employees make $50,000 per year and 5 employees make $75,000 per year.
What is the average (arithmetic mean) salary for the employees at ABC Company?
Explanation
The average is found by calculating the total payroll and then dividing by the total number of employees.
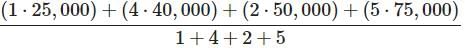
= 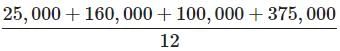
= 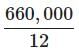
= $ 55,000
Report a problem
Question for Quantitative Practice Questions - 3
Try yourself:A tank has three inlet pipes. One, by itself, can fill the tank in one hour; another, by itself, can fill the tank in one hour and twenty minutes ; a third, by itself, can fill the tank in fifty minutes alone. If all three are on, then, to the nearest tenth of a minute, how long does it take to fill the tank?
Explanation
Think of this as a rate problem, with rate being measured in "tanks per minute".
Work = rate × time
The pipes can fill the tank up at rates of 1/60 ,1/80 , and 1/50 tanks per minute, respectively.
In the time t it takes to fill the tank, the three pipes fill up 1/60t of the tank, 1/80t of the tank, and 1/50t of the tank, respectively. Add the amounts of work done by the three tanks to get the total amount of work - one job.
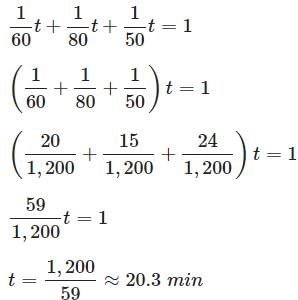
Report a problem
Question for Quantitative Practice Questions - 3
Try yourself:If Jack had twice the amount of money that he has, he would have exactly the amount necessary to buy 3 hamburgers at $0.96 apiece and 2 milk shakes at $1.28 apiece. How much money does Jack have?
Explanation
Let money Jack has be X.
Twice the money = 2X
Total money for 3 hamburgers = 3 x 0.96 = $2.88
Total money for 2 milk shakes = 2 x 1.28 = $2.56
2X = 2.88 + 2.56 = $5.44
X = 5.44/2 = $2.72
Answer C...
Report a problem
Question for Quantitative Practice Questions - 3
Try yourself: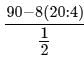
Explanation
(90 -8(20:4))/(1/2)
= (90-8(5))*2
= (90- 40)*2
= 50*2
= 100
Report a problem
Question for Quantitative Practice Questions - 3
Try yourself:Starting from point O on a flat school playground, a child walks 10 yards due north, then 6 yards due east, and then 2 yards due south, arriving at point P. How far apart, in yards, are points O and P?
Explanation
The distance in yards between points O and P is 10
The child creates a trapezoid with her walking pattern. The trapezoid can be divided into a rectangle and a right triangle
1) Find shape created by walking pattern. It will contain right angles (with compass points, "due [any direction]" = 90 degrees)
She walks 10 yards due north from point O to point A: OA = 10
Then 6 yards due east from A to B, which means a right angle at A. AB = 6
Then 2 yards due south from B to P. Another right angle. BP = 2
Connect P to O. She has created a trapezoid with her travel
2) Divide the shape into other shapes where distance between start and finish is easy to calculate
Draw a line from P, PX on diagram, that is perpendicular to OA
The new line divides trapezoid into two new shapes. Upper region is a rectangle. Lower region is right triangle
Rectangle has length = 6, width = 2
The rectangle's width, BP = AX = 2, divides original OA = 10 into two lengths AX and OX:
(OA - AX) = OX
(10 - 2) = 8 = OX
Looking at leg lengths PX and OX: the bottom portion is a 3-4-5 right triangle
3) Find distance between begin and end point
Find length of hypotenuse OP
Rule: If a right triangle has two legs in ratio 3x:4x, it is a 3x-4x-5x triangle and the hypotenuse = 5x
Leg PX = 6
Leg OX = (10 - 2) = 8
(3x: 4x: 5x) = (6: 8: 10)*
Distance between points O and P, in yards: 10
Answer (E)
Report a problem
Question for Quantitative Practice Questions - 3
Try yourself:At the rate of m meters per s seconds, how many meters does a cyclist travel in x minutes?
Explanation
We find the original rate, which is m meters per every s seconds, or m/s meters per second.
Since the number of seconds in a minute is 60, while we don't know how many seconds s is, we do know that to convert the rate in seconds to the rate in minutes we multiply by 60.
So, the rate per minute is 60m/s.
So, in x minutes, the cyclist will travel x * 60m/s = 60xm/s
The correct answer is E.
Alternative Method:
The greater m is, the further the cyclist will travel in a second or in x minutes. So m goes on top of the fraction.
We have m/ .
The greater s is, the slower the cyclist goes and the fewer meters traveled, because the greater s is the fewer meters the cyclist goes in 1 second. So, we put s on the bottom of the fraction.
We have m/s.
Since minutes have 60 seconds, to convert from rate per second to rate per minute, multiply by 60.
We have 60m/s.
The greater x is, the greater the number of meters traveled. So, put x on top of the fraction.
Final answer 60xm/s.
The correct answer is E.
Report a problem
Question for Quantitative Practice Questions - 3
Try yourself:If a person purchases 15 of the 3,000 tickets sold in a raffle that awards one prize, what is the probability that this person will not win?
Explanation
Let's use the complement: P(Event A happening) = 1 - P(Event A not happening)
Given: P(person wins) =15/3000
So, P(person does NOT win) 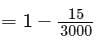
Simplify to get: P(person does NOT win) 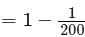
Rewrite with common denominator to get: P(person does NOT win) 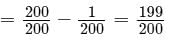
Answer: D
Report a problem
Question for Quantitative Practice Questions - 3
Try yourself: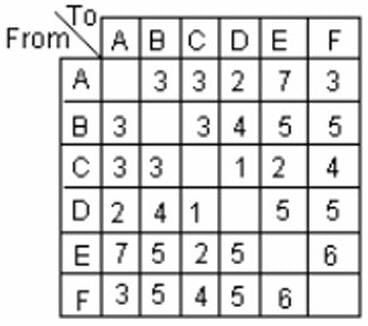
The table above shows the cost, in dollars, of traveling to and from cities A, B, C, D, E, and F. A sales representative wants to leave from A , travel to C, E, and F, and return to A. If the first city that the sales representative travels to must be E, what is the minimum possible cost for the entire trip?
Explanation
The sales representative has two options: 1) A-E-C-F-A and 2) A-E-F-C-A. Now let’s compare the costs of these two options:
Option 1: A-E-C-F-A
From A to E the cost is 7 dollars. From E to C it’s 2 dollars. From C to F it’s 4 dollars. From F to A it’s 3 dollars. The total spent is 16 dollars.
Option 2: A-E-F-C-A
From A to E the cost is 7 dollars. From E to F it’s 6 dollars. From F to C it’s 4 dollars. From C to A it’s 3 dollars. The total spend is 20 dollars.
We see that option 1 is cheaper, and the cost is 16 dollars.
Report a problem
Question for Quantitative Practice Questions - 3
Try yourself:The sum of n consecutive positive integers, where n > 1, is 2020. If n is odd, what is the value of n ?
Explanation
As n is odd, 2020n needs to divide without any remainders and will give us the median number. The only answer choices which divide 2020 without a remainder are B. 5 & D. 101.
Choice D. will not work. The median will be 2020/101=20 with 50 integers on either side. This means that the sequence will include zero and negative numbers, while we are told that the sum of n consecutive positive integers = 2020. Therefore, the answer has to be B.
To double check: 2020/5=404. With two numbers on either side, the sequence will be 402,403,404,405,406
Adding those numbers will give 2020.
Report a problem
Question for Quantitative Practice Questions - 3
Try yourself:A ball dropped from 36 m above the ground rebounds to 1/3rd of the height it falls from.If it continues to rebound in this manner, find the total distance the ball can cover?
Explanation
Report a problem
Question for Quantitative Practice Questions - 3
Try yourself:If a customer makes exactly one selection from each of the five categories shown in the table above, what is the greatest possible number of different ice cream sundaes that a customer can create?

Explanation
From 12 flavours, one flavour can be selected in = 12 ways
From 10 candies, one candy can be selected in = 10 ways
From 8 toppings, one topping can be selected in = 8 ways
From 5 nuts, one nut can be selected in = 5 ways
Total ways to order with/without cream = 2 ways
Total Possible combinations = 12*10*8*5*2 = 120*40*2 = 9600
Answer: Option A
Report a problem
Question for Quantitative Practice Questions - 3
Try yourself:On the number line, which of the following specifies the set of all numbers x such that |x - 3| + |x - 4| < 2?
Explanation
The x = 3 and x = 4 are the critical values to consider when we evaluate the absolute value expressions. According to the critical values, we have the following cases.
Case 1: x < 3
|x – 3| + |x – 4| < 2
(-x + 3) + (-x + 4) < 2
-2x + 7 < 2
5 < 2x
2.5 < x => 2.5 < x < 3 [We have to combine the solution with the constraint x < 3.]
Case 2: 3 ≤ x < 4
|x – 3| + |x – 4| < 2
(x – 3) + (-x + 4) < 2
1 < 2 => 3 ≤ x < 4 [Although the inequality 1 < 2 is true for all x, we have to consider the constraint 3 ≤ x < 4 as well.]
Case 3: 4 ≤ x
|x – 3| + |x – 4| < 2
(x – 3) + (x – 4) < 2
2x – 7 < 2
2x < 9
x < 4.5 => 4 ≤ x < 4.5 [We have to combine the solution with the constraint 4 ≤ x.]
Now, we have to join the three intervals we found in the three cases:
2.5 < x < 3
3 ≤ x < 4
4 ≤ x < 4.5
So, we have:
2.5 < x < 4.5
Report a problem
Question for Quantitative Practice Questions - 3
Try yourself:A positive number is mistakenly divided by 6 instead of being multiplied by 6. Based on the correct answer, the error thus committed, to the nearest percent, is:
Explanation
Let positive number be 6x.
Wrong = x
Right = 36x
Error = 35x
Error% = (Error/Right)*100 = (35x/36x)*100 = 97% (B)
Report a problem
Question for Quantitative Practice Questions - 3
Try yourself:A merchant paid $300 for a shipment of x identical calculators. The merchant used 2 of the calculators as demonstrators and sold each of the others for $5 more than the average (arithmetic mean) cost of the x calculators. If the total revenue from the sale of the calculators was $120 more than the cost of the shipment, how many calculators were in the shipment?
Explanation
Total Calculators = x
Cost per calculator = 300/x
Calculators sold = x - 2
Selling price per calculator 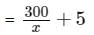
Total amount received 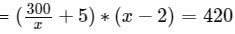
Solving,
x2 − 26x − 120 = 0
x = 30
Report a problem
Question for Quantitative Practice Questions - 3
Try yourself:The 38 movies in the video store fall into the following three categories: 10 action, 20 drama, and 18 comedy. However, some movies are classified under more than one category: 5 are both action and drama, 3 are both action and comedy, and 4 are both drama and comedy. How many action-drama-comedies are there?
Explanation
To find the number of movies that are action-drama-comedies, we use the principle of inclusion-exclusion.
Given:
- Total movies (T) = 38
- Action (A) = 10
- Drama (D) = 20
- Comedy (C) = 18
- Action and Drama (A ∩ D) = 5
- Action and Comedy (A ∩ C) = 3
- Drama and Comedy (D ∩ C) = 4
We need to find the number of movies that are in all three categories (A ∩ D ∩ C).
Using the principle of inclusion-exclusion:
∣A ∪ D ∪ C∣ = ∣A∣ + ∣D∣ + ∣C∣ − ∣A ∩ D∣ − ∣A ∩ C ∣ − ∣D ∩ C∣ + ∣A ∩ D ∩ C∣
Substitute the given values:
∣38 = 10 + 20 + 18 − 5 − 3 − 4 + ∣A ∩ D ∩ C∣
Simplify:
∣38 = 36 + ∣A ∩ D ∩ C∣
Solve for
∣A ∩ D ∩ C∣:
∣A ∩ D ∩ C∣ = 38 − 36
∣A ∩ D ∩ C∣ = 2
Thus, the number of action-drama-comedies is: 2
Report a problem
Question for Quantitative Practice Questions - 3
Try yourself:If X = 0.(81), where the brackets around the 2-digit sequence 81 indicates the sequence repeats indefinitely, what is the value of 99*X?
Explanation
We'll break our complex calculation (x99) into small, easy bits (x100 - x1)
This is a Precise approach.
100*X would be 81.818181818181 with infinite 81 after the decimal point.
That is, 100*X = 81.(81)
So 99*X 100*X - X = 81.(81) - 0.(81) = 81
(C) is our answer.
Report a problem