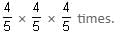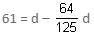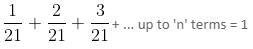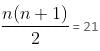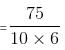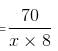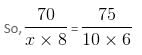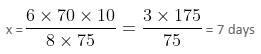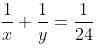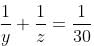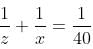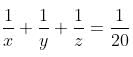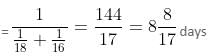This EduRev document offers 20 Multiple Choice Questions (MCQs) from the topic Time & Work (Level - 2). These questions are of Level - 2 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 2: Time & Work - 2
Try yourself:Stuart Little can eat 50 sweets in 4 days and Mickey Mouse can eat 42 sweets in 6 days. If both of them start together, what is the total number of sweets they can eat in 26 days?
Explanation
Stuart Little can eat 12.5 sweets in 1 day and Mickey Mouse can eat 7 sweets in 1 day.
It implies that together they can eat 19.5 sweets in 1 day.
Hence, 507 sweets will be eaten in 26 days.
Report a problem
Question for Practice Questions Level 2: Time & Work - 2
Try yourself:54 men can do a piece of work in 90 days, all working at the same rate. If 18 men leave after 62 days, how many days will the remaining men take to complete the work?
Explanation
Let the remaining work be completed in x days. Then, we get
54 × 90 = 54 × 62 + (54 – 18) × x
x = 42 days
Report a problem
Question for Practice Questions Level 2: Time & Work - 2
Try yourself:A is twice as efficient as B and B is twice as efficient as C. If A, B and C work together, a piece of work will be completed in 12 days. A and B work together for 8 days and thereafter, A is replaced by C.
How many more days are required to complete the work?
Explanation
Assume, C can do x work in 1 day; B can do 2x work in 1 day; and A can do 4x work in 1 day.
Total work = 12(x + 2x + 4x) = 84x
A and B work for 8 days, 8(2x + 4x) = 48x will be completed.
B and C can do 3x work in 1 day.
So, the remaining 36x can be completed in 12 days.
Report a problem
Question for Practice Questions Level 2: Time & Work - 2
Try yourself:Two pipes individually can fill a tank in 10 hours and 12 hours, while a third pipe can empty the full tank in 20 hours. In how much time will the tank be filled, if all three pipes operate together?
Explanation
In 1 hour, portion of tank filled
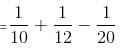
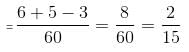
The tank will be filled in 15/2 hours = 7 hours and 30 minutes.
Report a problem
Question for Practice Questions Level 2: Time & Work - 2
Try yourself:A and B can do a piece of work in 20 and 30 days, respectively. A, B and C work together to complete the work. They get Rs. 9000 for completing the work. If they share the money according to the work done by them, then B will get Rs. 1500 more than the amount C gets. How much amount will A get?
Explanation
A can finish the work in 20 days.
B can finish the work in 30 days
Ratio of their one-day work = (1/20) : (1/30) = 3 : 2
If B gets Rs. x, then A will get Rs. 3/2x.
∴ 3/2x + x + (x - 1500) = 9000
⇒ x = 3000
A, B and C will get Rs. 4500, Rs. 3000 and Rs. 1500, respectively.
Report a problem
Question for Practice Questions Level 2: Time & Work - 2
Try yourself:P, Q and R can do a piece of work in 11 days, 10 days and 55 days, respectively. On which day will work be completed, if P is assisted by Q and R on alternate days?
Explanation
Suppose work is 550 units.
Work done by P and Q in 1 day = 50 + 55 = 105 units
Work done by P and R in 1 day = 50 + 10 = 60 units
Total work done in 2 days = 165 units
Total work done in 6 days = 165 x 3 = 495 units
Remaining work after 6 days = 550 - 495 = 55 units; which is completed on 7th day
Thus, the work will be completed on 7th day.
Report a problem
Question for Practice Questions Level 2: Time & Work - 2
Try yourself:There are two identical vessels X and Y. Y is filled with water to the brim and X is empty. There are two pots A and B such that B can hold half as much water as A can hold. One operation is said to be executed when water is transferred from Y to X using A and Y is replenished with water from X using B. If A can hold 1/2 litres of water and it takes 40 operations to equate the water levels in X and Y, then what is the capacity of Y?
Explanation
Let x, y, a, and b denote the volumes of X, Y, A, and B, respectively.
a = 1/2 litres
⇒ b = 1/4 litres
40 operations must have transferred (a - b) × 40 litres from Y to X, i.e.,
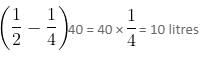
Now, there are 10 litres in X and 10 litres in Y.
Total volume = 10 + 10 = 20 litres
Capacity of Y = 20 litres
Report a problem
Question for Practice Questions Level 2: Time & Work - 2
Try yourself:20 men could do a piece of work in 30 days working 4 hours a day, 30 men worked for 20 days for 3 hours a day. Then all were laid off, except one. How many more days would it take the last man to complete the remaining work, working 10 hours a day?
Explanation
Let the work done by 1 man in 1 hour be m.
Thus, work done by 20 men working 4 hours a day in 30 days = 20 × 4 × m × 30 = Total work = W ... (i)
Now, working 3 hours a day for 20 days, work done by 30 men = 3 × 20 × 30 × m
Working 10 hours a day, let the last man take d more days.
Work done by the last man = 10 × d × m
Thus, total work done = 3 × 20 × 30 × m + 10 × d × m = W ... (ii)
So, from (i) and (ii), we have 20 × 4 × m × 30 = 3 × 20 × 30 × m + 10 × d × m
Or d = 60
Thus, the last man takes 60 days.
Hence, answer option 4 is correct.
Report a problem
Question for Practice Questions Level 2: Time & Work - 2
Try yourself:A team of 40 employees can complete a project in 60 days, working 6 hours a day. But because of deficiency of resources, only 20 employees can work for the first 20 days at 6 hours per day. Then, the resources are arranged. How many hours per day has the team of 40 employees got to work to complete the project on time?
Explanation
Let work done by 1 employee in 1 hour = w
Work done by 40 employees, working 6 hours a day, for 60 days = Total work = 40 × 6 × w × 60
Work actually done in first 20 days = 20 × 20 × 6 × w
Work left to be done = (40 × 6 × w × 60) - (20 × 20 × 6 × w) = 12,000w ...(i)
Let the 40 employees now work h hours per day for the rest of the 40 days.
So, work done by these 40 employees = 40 × 40 × h × w ...(ii)
On equating (i) and (ii), and solving for h, we get h = 7.5.
Thus, the employees now have to work 7.5 hours per day.
Thus, answer option 1 is correct.
Report a problem
Question for Practice Questions Level 2: Time & Work - 2
Try yourself:A can complete a piece of work in 4 days; B takes double the time taken by A; C takes double the time taken by B; and D takes double the time taken by C. They are paired in groups of two each. The first pair takes two-thirds of the time taken by the second pair to complete the work. Who make up the first pair?
Explanation
Amounts of work done in one day by A, B, C and D are 1/4, 1/8, 1/16, and 1/32, respectively.
Using options, we note that the pair of B and C does 3/16 of work in one day.
The pair of A and D does 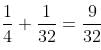 of the work in one day.
of the work in one day.
Hence, A and D take 32/9 days.
Report a problem
Question for Practice Questions Level 2: Time & Work - 2
Try yourself:Two pipes can fill a cistern in 20 minutes and 10 minutes, respectively. Third pipe can empty it in 25 minutes. Given that 1/5th of the cistern is already full, in how much time will the cistern be full if all three pipes are opened together?
Explanation
Two pipes can fill a cistern in 20 minutes and 10 minutes, respectively.
In one minute, pipes can fill 1/20 and 1/10 of the cistern, respectively.
Third pipe can empty it in 25 minutes.
In one minute, third pipe can empty 1/25 of the cistern.
1/5th of the cistern is already full, it means 4/5th remains empty.
In one minute, part of the cistern filled is:
Report a problem
Question for Practice Questions Level 2: Time & Work - 2
Try yourself:A is 60% more efficient than B. If A takes 9 days less than B to do a certain piece of work, then find the number of days it would take them to complete the same work, if both work together.
Explanation
The respective ratio of the efficiencies of A and B is 1.6 : 1 or 8 : 5.
Thus, times taken by A and B will be in the ratio of 1/8 : 1/5 or 5 : 8.
Let the times taken by A and B be 5x and 8x, respectively.
According to the problem, 5x = 8x - 9 or x = 3.
Thus, A and B can do the work in 15 days and 24 days, respectively.
If they work together, it will take them
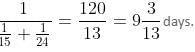
Report a problem
Question for Practice Questions Level 2: Time & Work - 2
Try yourself:'A' can construct a wall in 30 days, whereas 'B' can construct or destroy the same wall in the same time i.e. destroy time is equal to construct time. If 'A' constructs and 'B' destroys, it takes 60 days to construct the wall. How many days will it take to construct the wall, if both 'A' and 'B' work towards constructing the wall?
Explanation
Let us assume that 'B' can destroy the wall in 'd' days.
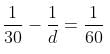
⇒ d = 60 days
So, if both 'A' and 'B' work to construct the wall,
In 1 day, they can do
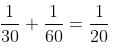
So, it takes 20 days to construct the wall, if both 'A' and 'B' work towards constructing the wall.
Report a problem
Question for Practice Questions Level 2: Time & Work - 2
Try yourself:Five men start a work at 8:00 a.m. so that they can complete the work by 4:00 p.m. If one more man is added at 12:00 noon, then at what time will the work be completed?
Explanation
Since five men can complete the work in 8 hours, (8:00 a.m. - 4:00 p.m.),
Number of man-hours required = 5 × 8 = 40
40 = 5 × 4 + 6 × H
⇒ H = 10/3 , or 3 hr 20 min
So, after 12:00 noon, it takes 3 hours and 20 minutes to complete the work.
Therefore, work will be completed at 3:20 p.m.
Report a problem
Question for Practice Questions Level 2: Time & Work - 2
Try yourself:A is 20% more efficient than B, but he works for five hours a day, whereas B works for 6 hours a day. If both A and B work together, they complete the work in 6 days. How many days are required to complete the work, if only A works for 3 hours a day?
Explanation
If B can do 'x' work per hour, A can do 1.2x.
Since A works only for 5 hours and B works for 6 hours, both can do the same amount of work in a day.
They together take 6 days to complete the work.
So, A alone takes 12 days working 5 hours a day.
So, he takes 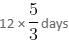 working 3 hours a day, i.e. 20 days.
working 3 hours a day, i.e. 20 days.
Report a problem
Question for Practice Questions Level 2: Time & Work - 2
Try yourself:Some men can do a piece of work in a certain number of days working for a certain number of hours a day. If the number of men, their efficiency and the working hours per day, all are increased by 25%, they complete their work in 61 days less time than estimated. What is the estimated number of days?
Explanation
In the second case, if the number of men, their efficiency and their working hours are all increased by 25% (i.e. 5/4 times), then the number of days required will be 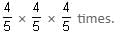
i.e. 64/125 times.
If 'd' is the number of estimated days, then according to question,
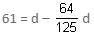
⇒ d = 125
Report a problem
Question for Practice Questions Level 2: Time & Work - 2
Try yourself:Fifteen men could finish a piece of work in 210 days. But at the end of every 10 days, 15 additional men are employed. In how many days will the work be finished?
Explanation
1 day-work of 15 men = 1/210
10 day-work of 15 men = 1/21
At the end of 10 days, 1/21 part will be finished; in the next 10 days, additional 2/21 part, and in the following 10 days, additional 3/21 part, and so on, will be finished.
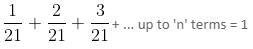
From Arithmetic Progression formula,
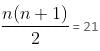
Or n = 6
Thus, the work will be finished in 10 × 6 = 60 days.
Report a problem
Question for Practice Questions Level 2: Time & Work - 2
Try yourself:If 6 men earn 10% of $750 in 10 days, then 8 men will earn 20% of $350 in
Explanation
Report a problem
Question for Practice Questions Level 2: Time & Work - 2
Try yourself:A and B can do a piece of work in 24 days. B and C can do a piece of work in 30 days. C and A can do a piece of work in 40 days. How long would they all take to do the same work together?
Explanation
Report a problem
Question for Practice Questions Level 2: Time & Work - 2
Try yourself:Mohan can do 1/2 a piece of work in 8 days, while Sohan can do 1/3 of the same work in 6 days. How long would it take for Mohan and Sohan to finish the work?
Explanation
Mohan can do half the work in 8 days.
∴ He can do the complete work in 16 days.
Sohan can do one-third of work in 6 days.
∴ He can do the complete work in 18 days.
Total time taken by both to finish the work together
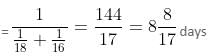
Report a problem

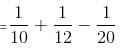
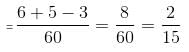
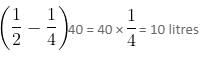
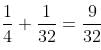 of the work in one day.
of the work in one day.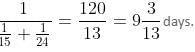
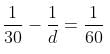
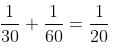
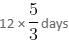 working 3 hours a day, i.e. 20 days.
working 3 hours a day, i.e. 20 days.