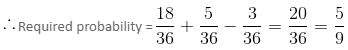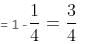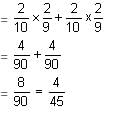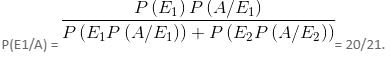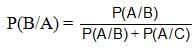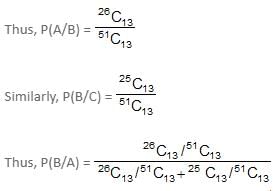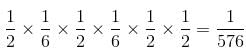This EduRev document offers 10 Multiple Choice Questions (MCQs) from the topic Probability (Level - 3). These questions are of Level - 3 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 3: Probability - 1
Try yourself:Two dice are rolled once. What is the probability of getting an even number on the first die or a total of 8?
Explanation
P(even number on Ist die or a total of 8) = P(even number on Ist die) + P(total of 8) – P(even number on Ist die and total of 8)
Now, P(even number of Ist die) = 18/36
Ordered pairs showing a total of 8 = {(6, 2), (5, 3), (4, 4), (3, 5), (2, 6)} = 5
∴ P(total of 8) = 5/36
P(even number of Ist die and total of 8) = 3/36
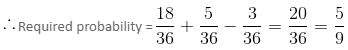
Report a problem
Question for Practice Questions Level 3: Probability - 1
Try yourself:If four coins are tossed, then what are the chances of getting two heads and two tails?
Explanation
Total number of outcomes = 24 = 16
Number of favourable outcomes = (HHTT), (HTHT), (HTTH), (TTHH), (THTH) and (THHT) = 6
Probability = 6/16 = 3/8
Report a problem
Question for Practice Questions Level 3: Probability - 1
Try yourself:Four robbers went to a safe place after a robbery. At midnight, each robber randomly chose one of the other three robbers and shot him. What is the probability that exactly two robbers were shot?
Explanation
Let the 4 robbers be A, B, C and D.
Now, A can choose any one out of the 3 robbers to shoot.
Same applies to B, C and D as well.
Thus, total number of ways in which the robbers can shoot each other = 3 × 3 × 3 × 3 = 34
Now, suppose B and C are shot.
So, A can shoot B or C, B can shoot C, C can shoot B, and D again can shoot B or C.
Thus, B and C can be shot in 2 × 2 = 4 ways.
Any two robbers who are selected can be shot in 4 ways.
Also, the number of ways in which the two robbers who are shot can be selected = 4C2
Hence, the total number of ways = 4C2 × 4/34 = 8/27
Thus, answer option 4 is correct.
Report a problem
Question for Practice Questions Level 3: Probability - 1
Try yourself:In a dice game, if a player rolls two dice, then his score will be the larger of the two numbers on the dice and if he rolls a doublet, his score will be the same number as the number in doublet. For example, if he rolls 4 and 6, his score will be 6 and if he rolls a doublet, e.g. 3 and 3, then his score will be 3. What is the probability that his score is 4 or more?
Explanation
When a player rolls two dice, there are 6 possibilities for the outcome on each dice.
So, there are 36 possibilities for the outcomes when two dice are rolled.
The possibilities that give a score of 3 or less are:
1 and 1, 1 and 2, 1 and 3, 2 and 1, 2 and 2, 2 and 3, 3 and 1, 3 and 2, 3 and 3.
So, 9 of the 36 possibilities give a score of 3 or less and the probability of getting 3 or less = 9/36 = 1/4
Thus, probability of getting 4 or more
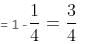
Report a problem
Question for Practice Questions Level 3: Probability - 1
Try yourself:Tickets are numbered 1 to 10. Two tickets are drawn one after the other at random. Find the probability that the number on one of the tickets is a multiple of 5 and the other is a multiple of 4.
Explanation
No. of tickets numbered from 1 to 10 divisible by 4 = 2
No. of tickets numbered from 1 to 10 divisible by 5 = 2
Let,
Event (A) : No. on one ticket is multiple of 5 and other multiple of 4
P(A) = (First ticket is multiple of 4 and other one of 5) + (First tickets is multiple of 5 and other one of 4)
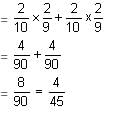
Report a problem
Question for Practice Questions Level 3: Probability - 1
Try yourself:Suppose that 5% of men and 0.25% of women have brown hair. A brown haired person is picked at random. What is the probability of this person being a male? Assume that there are equal number of men and women.
Explanation
E1 = Person selected is a man.
E2 = person selected is a woman.
A = Person selected is brown haired.
P(E1) = P(E2) = 1/2.
P(A/E1) = 5/100 = 1/20.
P(A/E2) = 1/400.
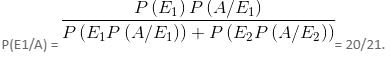
Report a problem
Question for Practice Questions Level 3: Probability - 1
Try yourself:A pack of playing cards contains 51 cards instead of 52 cards. The first 13 cards which were examined were all black, the probability that the missing card is red is
Explanation
Let A be the event that the 1st 13 cards drawn are all black.
Let B be the event that the missing card is Red.
Let C be the event that the missing card is Black.
By applying Baye's theorem,
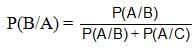
Now, when the missing card is Red, we have 26 Black cards and 25 Red cards with 51 cards in total.
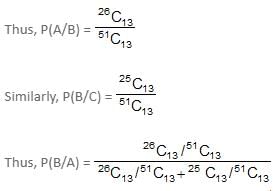
Report a problem
Question for Practice Questions Level 3: Probability - 1
Try yourself:Directions: Study the following information and answer the given question.
Three friends A, B and C do air rifle shooting as a hobby and compete against each other in friendly competitions. On a Sunday morning, they go to an empty tract of land along with their air rifles to shoot at clay practice targets from the distances of 100 m and 200 m. A hits his target 95% of the times from a distance of 100 m and 70% times from a distance of 200 m. The same figures for B are 85% and 80%, respectively. The same figures for C are 90% and 75%, respectively. They put in numbered chits (1, 2 and 3) to be drawn to decide the order of shooting and then each of them shoots at the targets turn-wise according to the chit number, first from 100 m and then from 200 m. They decide on a point system with 1 point for hitting the target from a distance of 100 m and 2 points for hitting it from a distance of 200 m with the winner getting a round of drinks paid by the other two.
Q. What is the probability that A will win the competition, given that all three of them manage to shoot at their targets from 100 m?
Explanation
A will win the competition if A manages to shoot from 200 m and B and C are unable to do so.
Thus, required probability = 0.70(1 - 0.80)(1 - 0.75) = 0.035
Report a problem
Question for Practice Questions Level 3: Probability - 1
Try yourself:Two cards are drawn at random from a pack of 52 cards. What is the probability that either both are red or both are jacks?
Explanation
S = Sample space.
n(S) = 52C2 = 1326.
A = event of getting both red cards and B = event of getting both jacks.
(A ∩ B) = event of getting jacks of red cards.
n(A) = 26C2 = 325.
n(B) = 4C2 = 6.
n(A ∩ B) = 2C2 = 1.
P(A) = 325/1326.
P(B) = 6/1326.
P(A ∩ B) = 1/1326.
P(A ∩ B) = P(A) + P(B) – P(A ∩ B) = 330/1326 = 55/221
Report a problem
Question for Practice Questions Level 3: Probability - 1
Try yourself:Directions: Read the given information and answer the following:
Two friends A and B play a game of chance. A person tosses a coin and if the coin shows a heads, he rolls a die. He does this twice and the score is the total of the numbers that the die throws up in both the rolls, if at all. If a person ends up with a tails on tossing the coin, he does not roll the die and his score is entered as 0. The winner of the game is the person whose score is the maximum.
Q. What is the probability that B will win with the maximum possible score and A scores 0?
Explanation
There shall be one case for the condition in the question to occur:
B scores 6 in both throws and A scores 0.
The probability for this is
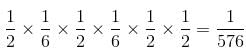
Report a problem