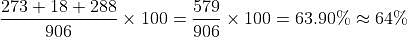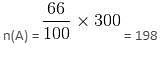This EduRev document offers 20 Multiple Choice Questions (MCQs) from the topic Set Theory (Level - 1). These questions are of Level - 1 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 1: Set Theory - 2
Try yourself:Directions: Study the following information and answer the question.
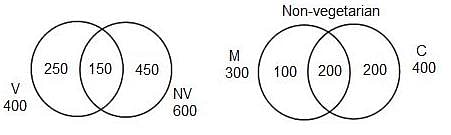
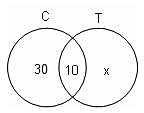
In Foodpur, where a person has to eat either vegetarian food or non-vegetarian food, there are 600 people who eat non-vegetarian food, 400 people who eat vegetarian food and 150 people who eat both. Of the people who eat non-vegetarian, there are 300 who eat mutton, 400 who eat chicken and 200 who eat both these types of meat.
Q. How many members of the city do not eat vegetarian food, but eat non-vegetarian food?
Explanation

From the diagram,
Number of people who do not eat vegetarian food, but eat non-vegetarian food = 450
Report a problem
Question for Practice Questions Level 1: Set Theory - 2
Try yourself:Directions: Study the following information and answer the question.
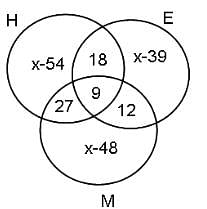
A newsagent sells the dailies Hindu, Express and Mail in equal number to 906 persons. 21 persons buy Express and Mail, 36 buy Hindu and Mail, 27 buy Hindu and Express, and buy 9 all the three dailies.
Q. The percentage of people buying Hindu or Express but not Mail is
Explanation
Since the dailies are sold in equal number, the total sale of each may be taken as x.
Hence, from the diagram, if we add up all the ''only'' regions, we get:
(x - 54) + (x - 48) + (x - 39) + 9 + 27 + 18 + 12 = 906
⇒ x = 327

Percentage of people buying Hindu or Express but not Mail =

Report a problem
Question for Practice Questions Level 1: Set Theory - 2
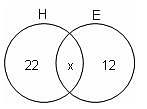
Try yourself:In a group of 45 students, 22 can speak Hindi only and 12 can speak English only. How many students can speak both Hindi and English?
Explanation

Number of students in the group = 45
Number of students who speak Hindi only = 22
Number of students who speak English only = 12
Let 'x' be the number of students who speak both Hindi and English.
22 + x + 12 = 45
x = 11
Report a problem
Question for Practice Questions Level 1: Set Theory - 2
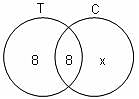
Try yourself:In a group of 26 persons, 8 take tea but not coffee and 8 take tea and coffee both. How many take coffee but not tea?
Explanation

T = Tea
C = Coffee
Let the number of people who like coffee but not tea be x.
Number of people in the group = 26
From the Venn diagram:
8 + 8 + x = 26
x = 10
Report a problem
Question for Practice Questions Level 1: Set Theory - 2
Try yourself:At a meeting of 100 people, there were 23 Indian men and 29 Indian women. Of these Indians, 4 were dentists and 24 were either men or dentists. Assume that there were no foreign dentists. How many foreigners attended the meeting?
Explanation
Out of 100, 23 are Indian men and 29 are Indian women.
So, the remaining 48 are foreigners.
Report a problem
Question for Practice Questions Level 1: Set Theory - 2
Try yourself:Let Na = {an : n ∈ N}. Then, N6 ∩ N8 is equal to
Explanation
N6 contains all multipliers of 6 and N8, those of 8. So, N6 ∩ N8 contains all those numbers which are common multiples of 6 and 8 both, i.e. multiples of 24 (LCM of 6 and 8 = 24).
So, N6 ∩ N8 = N24
Report a problem
Question for Practice Questions Level 1: Set Theory - 2
Try yourself:Let A and B have 3 and 6 elements, respectively. What can be the minimum number of elements in A ∪ B?
Explanation
A ∪ B will contain minimum number of elements if A ⊂ B; and in that case, n(A ∪ B) = n(B) = 6.
Report a problem
Question for Practice Questions Level 1: Set Theory - 2
Try yourself:In a group of 65 people, 40 like cricket, 10 like both cricket and tennis. Each one likes at least one sport out of cricket and tennis.
How many people like only tennis and not cricket?
Explanation

Total number of people = 65
Number of people who like cricket = 40
Number of people both cricket and tennis = 10
From the Venn diagram,
40 - 10 + 10 + x = 65
x = 25
Thus, number of people who like only tennis and not cricket = 25
Report a problem
Question for Practice Questions Level 1: Set Theory - 2
Try yourself:In a committee, 50 people speak French, 20 speak Spanish and 10 speak both Spanish and French. How many speak at least one of the two languages?
Explanation

Number of people who speak French = 50
Number of people who speak Spanish = 20
Number of people who speak both Spanish and French = 10
Number of people who speak at least one of the two languages = Number of people speaking only French + Number of people speaking only Spanish +
Number of people speaking both French and Spanish = (50 - 10) + 10 + (20 - 10) = 60
Report a problem
Question for Practice Questions Level 1: Set Theory - 2
Try yourself:In a community, 56% of the total families use mixers and 66% of the total use air conditioners.
If the total number of families is 300, what is the number of families using air conditioners only?
Explanation


n(M) + n(A) - n(M ∩ A) = n(M ∪ A)
n(M ∩ A) = 168 + 198 - 300 = 366 - 300 = 66
Number of families using air conditioners only = 198 - 66 = 132
Report a problem
Question for Practice Questions Level 1: Set Theory - 2
Try yourself:In a survey, students at a school were asked two questions. If 75% of the students answered the 1st question correctly, 55% answered the 2nd question correctly and 20% answered neither of the questions correctly, what percent of students answered both the questions correctly?
Explanation

Assuming 100 students:
n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
⇒100 – 20 = 75 + 55 – n(A ∩ B)
⇒ n(A ∩ B) = 50
Hence, 50% of the students answered both questions correctly.
Report a problem
Question for Practice Questions Level 1: Set Theory - 2
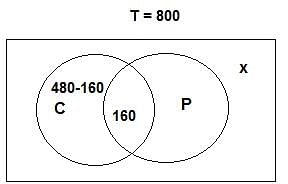
Try yourself:In a school with 800 students, 480 students are enrolled in Chemistry and 160 students are enrolled in both Chemistry and Physics. If the number of students who do not enrol in any of the subjects is equal to the one-seventh of the total number of students enrolled in Physics, then find how many students are not enrolled in either of them.
Explanation

Number of students in the school = 800
Number of students who are enrolled in Chemistry = 480
Number of students who are enrolled in both Chemistry and Physics = 160
∴ From the diagram,
480 + P + x = 800
[According to the question, 7x = P + 160 because x = (1/7)th of the total number of students enrolled in Physics]
Or, P = 7x - 160
⇒ 480 + 7x -160 + x = 800
⇒ 320 + 8x = 800
⇒ 8x = 480
⇒ x = 60
Hence, total number of students enrolled in neither Physics nor Chemistry = 60
Report a problem
Question for Practice Questions Level 1: Set Theory - 2
Try yourself:In a town of 10000 families, it was found that 40% families buy newspaper A, 20% families buy newspaper B and 10% families buy newspaper C, 5% families buy A and B, 3% buy B and C and 4% buy A and C. If 2% families buy all the three newspapers, then the number of families that buy none of these newspapers is
Explanation
Number of families who buy none of A, B and C = N - n(A ∪ B ∪ C),
where N = Total number of families.
n(A): Number of Newspaper A readers.
n(B): Number of Newspaper B readers.
n(C): Number of Newspaper C readers.
Number of families who buy none of A, B and C = 10000 - {n(A) + n(B) + n(C) - n(A ∩ B) - n(B ∩ C) - n(A ∩ C) + n(A ∩ B ∩ C)}
= 10000 - 4000 - 2000 - 1000 + 500 + 300 + 400 - 200
= 4000
Number of families who buy none of A, B and C = 4000
Report a problem
Question for Practice Questions Level 1: Set Theory - 2
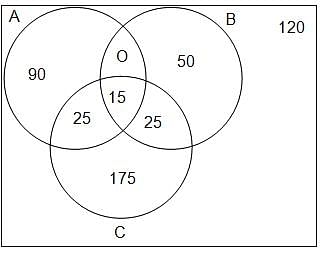
Try yourself:Directions: Study the given information and answer the following question.
In a survey of 500 customers, the numbers of customers who buy different grades of rice are given below:

Q. Which two among the following have the same frequency?
Explanation

A = 130 and B = 90
Option (2):
A only = 90 and B only = 50
Option (3):
'Both A and C, but not B' = 25 and 'Both B and C, but not A' = 25
Option (4):
'Both A and B' = 15 and 'Both B and C' = 40
So, option 3 is correct.
Report a problem
Question for Practice Questions Level 1: Set Theory - 2
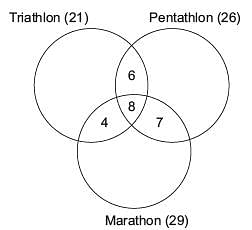
Try yourself:Directions: Study the following information and answer the question.
n the Indian athletic squad sent to the Olympics, 21 athletes were in the triathlon team; 26 were in the pentathlon team; and 29 were in the marathon team. 14 athletes can take part in triathlon and pentathlon; 12 can take part in marathon and triathlon; 15 can take part in pentathlon and marathon; and 8 can take part in all the three games.
Q. How many players are there in all?
Explanation
Since there are 14 players who are in triathlon and pentathlon, and there are 8 who take part in all three games, there will be 6 who take part in only triathlon and pentathlon. Similarly,
Only triathlon and marathon = 12 – 8=4 & Only Pentathlon and Marathon = 15 – 8 = 7.

The figure above can be completed with values for each sport (only) plugged in:
The answers would be: 3 + 6 + 8 + 4 + 5 + 7 + 10 = 43.
Option (b) is correct.
Report a problem