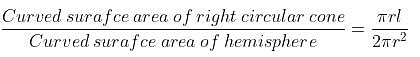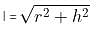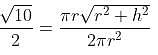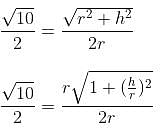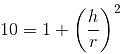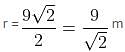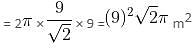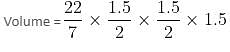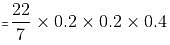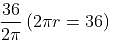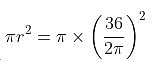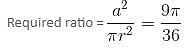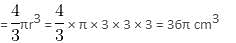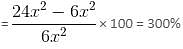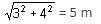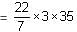This EduRev document offers 10 Multiple Choice Questions (MCQs) from the topic Mensuration (Level - 1). These questions are of Level - 1 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 1: Mensuration - 1
Try yourself:The height of a cylinder is 14 cm and its curved surface area is 264 sq. cm. Find the radius of its base.
Explanation
Curved surface area of a cylinder = 2πrh
Given: h = 14 cm and curved surface area = 264 cm2
∴ 2πrh = 264
r = 3 cm
Report a problem
Question for Practice Questions Level 1: Mensuration - 1
Try yourself:The curved surface areas of a right-circular cone and a hemisphere, having the same radius are in the ratio of  Find the ratio of the height of the cone to the radius of the hemisphere.
Find the ratio of the height of the cone to the radius of the hemisphere.
Explanation
Report a problem
Question for Practice Questions Level 1: Mensuration - 1
Try yourself:If a square is rotated along one of its diagonals, then find the curved surface area of the shape formed by it, given that one of its side is 9 metres.
Explanation
According to the question, rotating square along a diagonal makes two right-circular cones.
As the diagonal makes a right-angled triangle by the sides of square, so
D = 9√2 m (Using Pythagoras theorem)

So, curved surface area of the cone = 2 πrl

Report a problem
Question for Practice Questions Level 1: Mensuration - 1
Try yourself:If the diameter of a cylindrical drum is 1.5 m and the height is 1.5 m, then maximum how many smaller aluminium cylindrical cans can be completely filled by the liquid in the cylindrical drum, if the radius and height of each can are 0.2 metres and 0.4 metres, respectively?
Explanation
According to the question:
Volume of the drum = πr2h

Volume of small can

Divide both the above volumes to get the maximum number of cans as 52.73, i.e. maximum 52 cans can be completely filled.
Report a problem
Question for Practice Questions Level 1: Mensuration - 1
Try yourself:A steel wire is bent in the shape of a square having semi-perimeter as 18 cm and an area of 81 cm2, and then the same wire is again bent to make a circle. Find the ratio of the area of square to that of circle.
Explanation
Report a problem
Question for Practice Questions Level 1: Mensuration - 1
Try yourself:In a swimming pool measuring 90 m by 40 m, 150 men take a dip. If the average displacement of water by a man is 8 cubic metres, what will be the approximate rise in water level?
Explanation
Volume of water displaced by 150 men = 150 × 8 = 1200 m3
Let the rise in water level be x.
90 × 40 × x = 1200
⇒ x = 12/36 = 1/3 or 0.33 m = 33.33 cm (Approx.)
Report a problem
Question for Practice Questions Level 1: Mensuration - 1
Try yourself:A sphere of diameter 6 cm is dropped into a right circular cylindrical vessel, partly filled with water. The diameter of the cylindrical vessel is 12 cm. If the sphere is completely submerged in water, by how much will the level of water rise in the cylindrical vessel?
Explanation
Radius of the sphere = 6/2 = 3 cm
Radius of the cylinder = 12/2 = 6cm
Volume of the sphere

New volume of the cylindrical vessel - Initial volume of the cylindrical vessel = Volume of the sphere
Initial height = h cm
Final height = H cm
πr2H - πr2h = 36π
Report a problem
Question for Practice Questions Level 1: Mensuration - 1
Try yourself:Three metal cubes having volumes 125 cubic cm, 64 cubic cm and 27 cubic cm are melted to form a new cube. Find the value of edge of the new cube.
Explanation
Since three metal cubes of volumes 125 cm3, 64 cm3 and 27 cm3 are melted to form a new cube,
Therefore, volume of the new cube = 125 + 64 + 27 = 216 cm3
Total volume = 216 cm3
a3 = 216 cm3
a3 = 63
On comparing, we get
a = 6
Edge = 6 cm
Report a problem
Question for Practice Questions Level 1: Mensuration - 1
Try yourself:The percentage increase in the surface area of a cube, when each side is doubled, is
Explanation
Let each side of the cube be x cm.
Therefore, surface area = 6x2
Surface area of the cube after making the side of cube double = 6(2x)2 = 24x2
So, clearly, it becomes 4 times of the previous one.
Percentage increase

Report a problem
Question for Practice Questions Level 1: Mensuration - 1
Try yourself:A circus tent is in the form of a cone over a cylinder. The diameter of the base is 6 m, the height of the cylindrical part is 15 m and the total height of the tent is 19 m. The canvas required for the tent is
Explanation
Height of the cylinder = 15 m
Height of the cone, 'h' = 19 - 15 = 4 m
Radius = 6/2 = 3 m
Slant height of the cone = 
Canvas required = C.S.A. of (cone + cylinder)
= πrl + 2πrH
= πr(5 + 2 × 15)

= 330 m2
Report a problem
 Find the ratio of the height of the cone to the radius of the hemisphere.
Find the ratio of the height of the cone to the radius of the hemisphere.