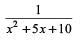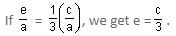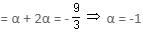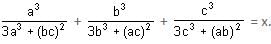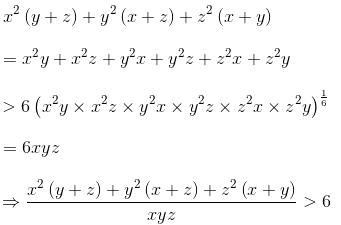This EduRev document offers 15 Multiple Choice Questions (MCQs) from the topic Quadratic Equations & Linear Equations (Level - 1). These questions are of Level - 1 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 1: Quadratic Equations & Linear Equations - 2
Try yourself:If the difference between the roots of the equation x2 - 5x + 2k = 1 is 3, then find the value of k.
Explanation
The given equation can be written as x2 - 5x + (2k - 1) = 0.
If p and q are the roots, it is given that p - q = 3.
⇒ (p + q)2 - 4pq = 9. (∵ (p - q)2 = (p + q)2 - 4pq)
⇒ 25 - 4(2k - 1) = 9 (∵ p + q = 5, pq = 2k - 1)
∴ k = 2.5
Report a problem
Question for Practice Questions Level 1: Quadratic Equations & Linear Equations - 2
Try yourself:If x = 3 + √8, then find the value of x2 + (1/x2).
Explanation
Given: x = 3 + √8
1/x = 1/(3 + √8) = (3 - √8)/[32 - (√8)2] = 3 - √8/(9 - 8) = 3 - √8
x + 1/x = 3 +√8 + 3 - √8 = 6
Squaring both sides, we get:
(x + 1/x)2 = 62
x2 + 1/x2 + 2 = 36
x2 + 1/x2 = 36 - 2 = 34
Report a problem
Question for Practice Questions Level 1: Quadratic Equations & Linear Equations - 2
Try yourself:If the polynomial ax4 + bx3 + cx2 + dx + e has the property that the product of its roots is 1/3rd of the sum taking two roots at a time, then find the relationship between e and c.
Explanation
Product of all the roots = e/a
Sum of the roots taking two at a time = c/a
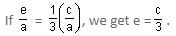
Report a problem
Question for Practice Questions Level 1: Quadratic Equations & Linear Equations - 2
Try yourself:If (c - 3)2 = c2 + kc + 9, then the value of k is:
Explanation
Given, (c - 3)2 = c2 + kc + 9
We know the formula: (a - b)2 = a2 - 2ab + b2
Applying the above formula, we get
c2 - 6c + 9 = c2 + kc + 9
Comparing both sides, we get
k = -6
Report a problem
Question for Practice Questions Level 1: Quadratic Equations & Linear Equations - 2
Try yourself:Find x + y + z if 5x + 9y + 13z = 50 and 24x + 20y + 16z = 66.
Explanation
5x + 9y + 13z = 50 and 24x + 20y + 16z = 66
Adding both, we get
29x + 29y + 29z = 116
Thus, x + y + z = 4
Report a problem
Question for Practice Questions Level 1: Quadratic Equations & Linear Equations - 2
Try yourself:Find the nature of roots of the following equations:
(i) x2 + 9x + 27 = 0
(ii) 6x2 - 13x - 5 = 0
Explanation
(i) x2 + 9x + 27 = 0
D = 92 - 4(27)
D < 0; therefore, roots are imaginary.
(ii) 6x2 - 13x - 5 = 0
D = (-13)2 - 4(-5)(6)
D > 0; therefore, roots are real.
So, option (3) is the correct answer.
Report a problem
Question for Practice Questions Level 1: Quadratic Equations & Linear Equations - 2
Try yourself:If the roots of the equation 3x2 + 9x + k = 0 are in the ratio of 1 : 2, then what is the value of k?
Explanation
Since the roots are in the ratio of 1 : 2, they can be assumed as α and 2α.
Sum of the roots
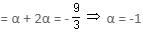
Product of the roots = α (2α) = k/3 ⇒ k = 6
Report a problem
Question for Practice Questions Level 1: Quadratic Equations & Linear Equations - 2
Try yourself:Find the value of (x – a)(x – b)(x – c) … (x – z).
Explanation
The 24th term in the series will be (x – x).
Now, (x – x) = 0
So, (x – a)(x – b) … (x – z) = 0.
Report a problem
Question for Practice Questions Level 1: Quadratic Equations & Linear Equations - 2
Try yourself:After 15 years, Ralph's age will be five times his age 5 years back. What is the present age of Ralph?
Explanation
Let Ralph's present age be x years.
After 15 years, his age will be (x + 15) years. His age 5 years back was (x - 5) years.
According to the condition: x + 15 = 5(x - 5)
On solving, we get x = 10.
Therefore, Ralph's present age = 10 years
Report a problem
Question for Practice Questions Level 1: Quadratic Equations & Linear Equations - 2
Try yourself:a, b and c are three integers and they are not equal to each other. If a + b + c = 1, provided one of them is equal to zero, then the value of 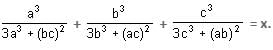 Here, x will be equal to
Here, x will be equal to
Explanation
Since one of a, b, c is equal to zero, we can put the values of a, b and c as a = 2, b = -1, c = 0 in the following equation
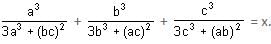
On solving we get x = 2/3.
Report a problem
Question for Practice Questions Level 1: Quadratic Equations & Linear Equations - 2
Try yourself:If x, y, z are distinct positive real numbers, then 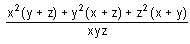 would be
would be
Explanation
Since, x, y, z are distinct positive real numbers, use AM > GM
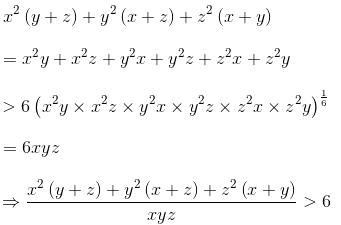
Hence, option (3) is correct.
Report a problem
Question for Practice Questions Level 1: Quadratic Equations & Linear Equations - 2
Try yourself:Find the maximum value of the expression
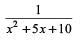
Explanation
For the given expression to be a maximum, the denominator should be minimized. (Since, the function in the denominator has imaginary roots and is always positive). x2 + 5x + 10 will be minimized at x = – 2.5 and its minimum values at x = –2.5 is 3.75. Hence, required answer = 1/3.75 = 4/15.
Report a problem
Question for Practice Questions Level 1: Quadratic Equations & Linear Equations - 2
Try yourself:Find the minimum value of the expression (p +1/p); p > 0.
Explanation
The minimum value of ( p + 1/p) is at p = 1. The value is 2.
Report a problem
Question for Practice Questions Level 1: Quadratic Equations & Linear Equations - 2
Try yourself:If the roots of equation x2 + bx + c = 0 differ by 2, then which of the following is true?
Explanation
To solve this take any expression whose roots differ by 2.
Thus, (x – 3) (x – 5) = 0
⇒ x2 – 8x + 15 = 0
In this case, a = 1, b = –8 and c = 15.
We can see that b2 = 4(c + 1).
Report a problem
Question for Practice Questions Level 1: Quadratic Equations & Linear Equations - 2
Try yourself:If f(x) = (x + 2) and g(x) = (4x + 5), and h(x) is defined as h(x) = f(x) · g(x), then sum of roots of h (x) will be
Explanation
h (x) = 4x2 + 13x + 10.
Sum of roots -13/4.
Report a problem
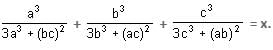 Here, x will be equal to
Here, x will be equal to
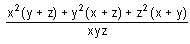 would be
would be