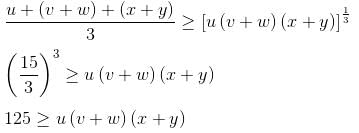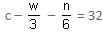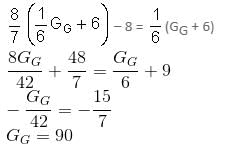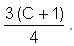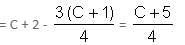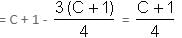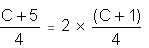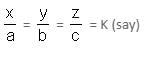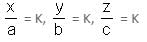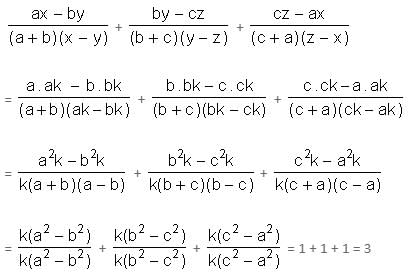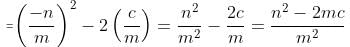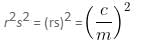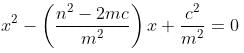This EduRev document offers 15 Multiple Choice Questions (MCQs) from the topic Quadratic Equations & Linear Equations (Level - 3). These questions are of Level - 3 difficulty and will assist you in the preparation of CAT & other MBA exams. You can practice/attempt these CAT Multiple Choice Questions (MCQs) and check the explanations for a better understanding of the topic.
Question for Practice Questions Level 3: Quadratic Equations & Linear Equations
Try yourself:If u + v + w + x + y = 15, then what is the maximum value of uvx + uvy + uwx + uwy?
Explanation
Given: u + v + w + x + y = 15
We need the maximum value of uvx + uvy + uwx + uwy.
(uv + uw)(x + y) = u(v + w)(x + y)
Let's use AM ≥ GM in u, (v + w), (x + y):
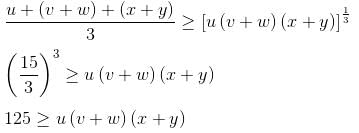
Hence, the maximum value of uvx + uvy + uwx + uwy is 125.
Report a problem
Question for Practice Questions Level 3: Quadratic Equations & Linear Equations
Try yourself:Which of the following relationships is correct, if α and β are the roots of |x|2 + |x| - 6 = 0?
Explanation
Put |x| = y.
Given equation: y2 + y - 6 = 0
On solving, we get y = 2 or -3
i.e. |x| = 2 or -3
Modulus cannot be negative.
Therefore, |x| = 2
⇒ The roots (α and β) of the equation are 2 and -2.
Hence, α + β = 0
Report a problem
Question for Practice Questions Level 3: Quadratic Equations & Linear Equations
Try yourself:If the minimum value of f(x) = x2 + 2bx + 2c2 is greater than the maximum value of g(x) = -x2 - 2cx + b2, then (x being real)
Explanation
For real x, f(x) = x2 + 2bx + 2c2
= x2 + 2bx + b2 + 2c2 - b2
= (x + b)2 + 2c2 - b2 ≥ 2c2 - b2
and g(x) = -x2 - 2cx + b2
= -(x2 + 2cx + c2) + b2 + c2
= b2 + c2 - (x + c)2 ≤ b2 + c2
Hence, min. f(x) > max. g(x)
if 2c2 - b2 > b2 + c2
i.e. if c2 > 2b2
Report a problem
Question for Practice Questions Level 3: Quadratic Equations & Linear Equations
Try yourself:The values of a for which one root of the equation x2 - (a + 1)x + a2 + a - 8 = 0 exceeds 2 and the other is less than 2, are given by
Explanation
If the roots of the given equation are α and β, then α > 2 and β < 2.
⇒ α - 2 > 0 and β - 2 < 0
⇒(α - 2)(β - 2) < 0
⇒ αβ - 2(α + β) + 4 < 0
⇒ a2 + a - 8 - 2(a + 1) + 4 < 0
(∵ α + β = a + 1 and αβ = a2 + a - 8)
⇒ a2 - a - 6 < 0
⇒ (a - 3)(a + 2) < 0
⇒ -2 < a < 3
Report a problem
Question for Practice Questions Level 3: Quadratic Equations & Linear Equations
Try yourself:A test has 50 questions. A student scores 1 mark for a correct answer, –1/3 for a wrong answer and –1/6 for not attempting a question. If the net score of a student is 32, then the number of questions answered wrongly by that student cannot be less than
Explanation
Let c, w and n be the number of questions answered correctly, wrongly and not attempted, respectively.
∴ c + w + n = 50 … (i)
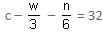
6c – 2w – n = 32 × 6 = 192 … (ii)
Adding equations (i) and (ii), we have
7c – w = 242
w = 7c – 242
Since w and c are positive numbers, the minimum value of c for which w is positive is 35.
Hence, w = 3
Report a problem
Question for Practice Questions Level 3: Quadratic Equations & Linear Equations
Try yourself:Which of the following conditions must p, q and r satisfy so that the following system of linear simultaneous equations has at least one solution, such that p + q + r ≠ 0?
x + 2y - 3z = p
2x + 6y - 11z = q
x - 2y + 7z = r
Explanation
Multiply the first equation by 5, second by -2 and third by -1.
5x + 10y - 15z = 5p ... (i)
-4x - 12y + 22z = - 2q ... (ii)
-x + 2y - 7z = - r ... (iii)
Adding all three equations, we get
5p - 2q - r = 0
Report a problem
Question for Practice Questions Level 3: Quadratic Equations & Linear Equations
Try yourself:Ghosh Babu said to Banke Lal, "My wife is six years older than your daughter. Your daughter is one-sixth the age of my great-grandfather. But, your eldest son is younger than your second wife by eight years." Banke Lal replied, "My second wife is older than your only wife by one-seventh. My eldest son is one-sixth the age of what your great-grandfather would have been today, had he not died six years ago.'' What would have been the age of Ghosh Babu's great-grandfather at the time of this conversation?
Explanation
Report a problem
Question for Practice Questions Level 3: Quadratic Equations & Linear Equations
Try yourself:Four dog dealers purchased some dogs. The first dealer purchased 1 Airedale, 3 Spaniels and 7 puppies and paid $1400; and the second purchased 1 Airedale, 4 Spaniels and 10 puppies and paid $1700. The third purchased 10 Airedales, 15 Spaniels and 25 puppies; and the fourth purchased 1 Airedale, 1 Spaniel and only 1 puppy. How much did the third and fourth dealers pay, separately?
Explanation
a + 3s + 7p = 1400 … (1)
a + 4s + 10p = 1700 … (2)
10a + 15s + 25p = ?
And a + s + p = ?
We have 2 equations and 3 unknown variables.
Subtracting equation (1) from (2), we get
s + 3p = 300
And 4 × equation (1) - 3 × equation (2) gives a - 2p = 500.
a + s + p = 800
Also, 10a - 20p = 5000
And 15s + 45p = 4500
10a + 15s + 25p = 9500
Report a problem
Question for Practice Questions Level 3: Quadratic Equations & Linear Equations
Try yourself:Three drunkards agreed to pool their vodka and decided to share it with the fourth drunkard (who had no vodka) at a price equal to 5 roubles a litre. The first drunkard contributed 1 litre more than the second and the second contributed 1 litre more than the third. Then, all four of them divided the vodka equally and drank it. The fourth drunkard paid money, which was divided in the ratio of each drunkard's contribution towards his portion. It was found that the first drunkard got twice as much money as the second. How much money did the second drunkard get (in roubles)?
Explanation
Report a problem
Question for Practice Questions Level 3: Quadratic Equations & Linear Equations
Try yourself:Rocky and Anthony are solving a quadratic equation. While solving, Rocky commits a mistake in the constant term and finds the roots to be 8 and 2. Anthony commits a mistake in the coefficient of X and finds the roots to be -9 and -1. Find the correct roots.
Explanation
Let the correct equation be X2 + aX + b = 0 … (1)
Roots found by Rocky are 8 and 2. As such, the equation should be X2 - (8 + 2)X + 8 2 or X2 - 10X + 16 = 0.
Since he has committed a mistake only in the constant term, coefficient of X in both would be the same, or a = -10.
Now, roots found by Anthony are -9 and -1. As such, the equation should be X2 - (-9 - 1)X + (-9)(-1) = 0 or X2 + 10X + 9 = 0.
As he has committed mistake only in the coefficient of X, therefore constant term in equation (1) and his solution would be the same, i.e. b = 9. Hence, the correct equation is X2 - 10X + 9 = 0 or (X - 9)(X - 1) = 0.
So, the roots are 9 and 1.
Report a problem
Question for Practice Questions Level 3: Quadratic Equations & Linear Equations
Try yourself:
Explanation
Report a problem
Question for Practice Questions Level 3: Quadratic Equations & Linear Equations
Try yourself:If r and s are the solutions of quadratic equation mx2 + nx + c = 0, which of the following equations can have its roots equal to r2 and s2?
Explanation
Report a problem
Question for Practice Questions Level 3: Quadratic Equations & Linear Equations
Try yourself:It is known that y2 - 11y + 4k = 0 has two distinct roots. It is also known that one factor is (y - k) and k is greater than zero. What is the difference between the sum and products of the roots?
Explanation
Since (y - k) is a factor of the quadratic equation, so substitute y = k in the equation.
So the equation y2 - 11y + 4k = 0 transforms to k2 - 11k + 4k = 0
Hence, k2 = 7k and k = 7.
Now, substitute k = 7 in the equation y2 - 11y + 4k = 0
The equation becomes y2 - 11y + 28 = 0, the roots of which are 7 and 4.
Sum of the roots = 11;
Product of roots = 28
So, required difference = 28 - 11 = 17
Report a problem
Question for Practice Questions Level 3: Quadratic Equations & Linear Equations
Try yourself:A harvester's team had to harvest 170 hectares of a field. For the first four days, the team harvested as per the plan. After that, they started harvesting at double the rate planned for every day. So, the work was finished eight days before the planned date. How many hectares had to be harvested by the team each day as per the initial plan?
Explanation
Suppose, according to the initial plan, 'a' hectares of land were to be harvested each day and 'd' days were to be taken for the complete job.
So, ad = 170 ... (i)
Now, the equation formed for the new situation is as follows.
4a + (d - 4 - 8)2a = 170
Or, 4a + 2ad - 24a = 170 ... (ii)
Plugging in the value of ad as 170 from equation (i) into equation (ii), we get 4a + 2 × 170 - 24a = 170
Or, a = 8.5
Thus, 8.5 hectares had to be harvested by the harvesting team each day according to the initial plan.
Hence, answer option 2 is correct.
Report a problem
Question for Practice Questions Level 3: Quadratic Equations & Linear Equations
Try yourself:36 coins are divided among A, B, C and D, such that B takes more than A, C takes more than B and D takes more than C. If the difference in the number of coins between A and B is 1, between B and C is 9 and between C and D is 7, the number of coins with A is
Explanation
Let the numbers of coins with A, B, C and D be a, b, c and d, respectively.
Now, according to the question:
a + b + c + d = 36 … (1)
And d > c > b > a (Given)
b - a = 1 … (2)
⇒ b = a + 1
c - b = 9 … (3)
Add (2) and (3).
c - a = 10 … (4)
⇒ c = a + 10
d - c = 7 … (5)
Add (4) and (5).
d - a = 17
d = a + 17
The total numbers of coins is 36.
a + a + 1 + a + 10 + a + 17 = 36
⇒ 4a + 28 = 36
⇒ 4a = 8
⇒ a = 2
Report a problem