Triangles Class 9 Notes Maths Chapter 6
| Table of contents |

|
| Introduction |

|
| Congruence of Triangles |

|
| Criteria for Congruence of Triangles |

|
| Some Properties of a Triangle |

|
| Some More Criteria for Congruence of Triangles |

|
Introduction
A triangle, a closed figure formed by three intersecting lines, is characterized by three sides, three angles, and three vertices.
 The term 'triangle' is derived from 'tri,' signifying 'three.' For instance, in triangle ABC (denoted as ∆ ABC), AB, BC, and CA represent the three sides, while ∠ A, ∠ B, ∠ C are the corresponding angles, and A, B, and C are the vertices.
The term 'triangle' is derived from 'tri,' signifying 'three.' For instance, in triangle ABC (denoted as ∆ ABC), AB, BC, and CA represent the three sides, while ∠ A, ∠ B, ∠ C are the corresponding angles, and A, B, and C are the vertices.
Congruence of Triangles
In our daily experiences, we encounter identical objects like photographs, bangles, and ATM cards, which are called congruent figures. The term 'congruent' implies equality in all respects, indicating figures with identical shapes and sizes. When two circles, squares, or equilateral triangles of the same dimensions overlap, we observe complete coverage, confirming them as congruent circles, congruent squares, and congruent equilateral triangles, respectively.
Real-life Applications
The study of congruence extends beyond theoretical concepts. For example:
- In ice trays, the molds for making ice are congruent, facilitating uniformity.
- The concept of congruence is applied in creating casts for identical objects, ensuring consistency.
A triangle has three sides, three angles, and three vertices.
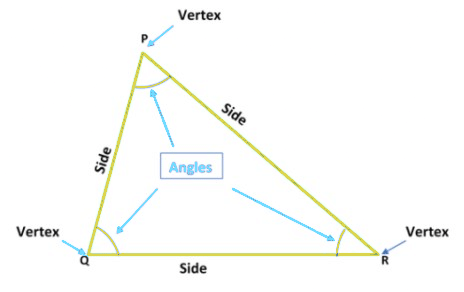
For example, in the triangle PQR, PQ, QR, and RP are the three sides, ∠QPR, ∠PQR, ∠PRQ are the three angles and P, Q and R, are the three vertices.
 A triangle is a unique figure; it is everywhere around us. We can see the sandwiches in the shape of a triangle, traffic signals, cloth anger, set squares, etc. All these are in the shape of a triangle.
A triangle is a unique figure; it is everywhere around us. We can see the sandwiches in the shape of a triangle, traffic signals, cloth anger, set squares, etc. All these are in the shape of a triangle.
Correspondence Importance
When establishing congruence, correct correspondence between vertices is essential. For example:
- In ∆ FDE ≅ ∆ ABC, FD ↔ AB, DE ↔ BC, and EF ↔ CA.
- However, writing ∆ DEF ≅ ∆ ABC is incorrect due to improper correspondence.
Note: In congruent triangles, corresponding parts are equal. The acronym CPCT (Corresponding Parts of Congruent Triangles) is often used to denote this equality.
Symbolic Representation
Symbolically, ∆ PQR ≅ ∆ ABC is expressed as:
- PQ covers AB, QR covers BC, RP covers CA.
- ∠ P covers ∠ A, ∠ Q covers ∠ B, ∠ R covers ∠ C.
- Vertices correspond: P ↔ A, Q ↔ B, R ↔ C.
In the figures shown above, each pair is identical to each other. Such figures are called congruent (they are similar and fit over one another exactly).
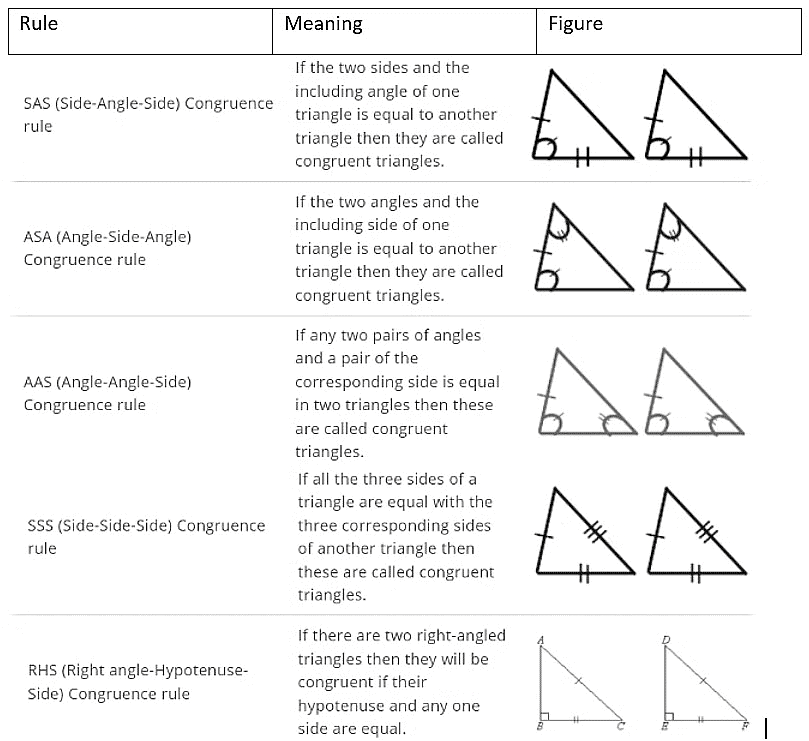
Criteria for Congruence of Triangles
Axiom 1: Side-Angle-Side (SAS) congruence rule
(An axiom is a mathematical statement that is assumed to be true without proof.)
Two triangles are congruent if two sides and the included angle of one triangle are equal to the two sides and the included angle of the other triangle.
Given: Two triangles ABC and PQR such that AB = PQ, AC = PR and ∠BAC = ∠QPR.
To prove: ∆ ABC ≅ ∆ PQR.
Proof: This result cannot be proved with help of previously known results. So, this rule is accepted as an axiom.
Another way to check whether the given two triangles are congruent or not, we follow a practical approach.
Place ∆ABC over ∆PQR such that the side AB falls on side PQ, vertex A falls on vertex P and B on Q. Since ∠BAC = ∠QPR. Therefore, AC will fall on PR. But AC = PR and A falls on P. therefore, C will fall on R. Thus, AC coincides with PR.
Now, B falls on Q and C falls on Therefore, BC coincides with QR.
Thus, ∆ ABC when superposed on ∆ PQR, covers it exactly. Hence, by the definition of congruence, ∆ ABC ≅ ∆ PQR.
Example 1: Check whether ∆ABC and ∆PQR are congruent or not.

Solution: In ∆ ABC and ∆ PQR, we have
AB = PQ = 5 cm (Given)
∠ BAC = ∠QPR = 40o (Given)
AC = PR = 4 cm (Given)
Therefore, ∆ ABC ≅ ∆ PQR (By SAS criterion of congruence)
Example 2: In the figure below, R is the mid-point of PT and SQ. Prove that ∆ PQR ≅ ∆ TSR.

Given: PR = RT and SR = RQ.
To prove: ∆ PQR ≅ ∆ TSR.
Proof: In ∆ PQR and ∆ TSR, we have
PR = TR (R is the mid-point of PT)
∠PRQ = ∠TRS (Vertically opposite angles are equal)
QR = SR (R is the mid-point of SQ)
Therefore, Δ PQR ≅ Δ TSR (By SAS-criterion of congruence)
Example 3: In the figure, it is given that PT = PU and QT = RU. Prove that ΔPTR ≅ ΔPUQ
Given: PT = PU and QT = RU.
To prove: Δ PTR ≅ Δ PUQ.
Proof: We have,
PT = PU ........... (I)
And, QT = RU .......... (II)
Adding equation (I) and (II), We get,
PT + QT = PU + RU
⇒ PQ = PR ........... (III)
Now, in ∆ PTR and ∆ PUQ, we have
PT = PU [Given]
⇒ ∠ TPR = ∠UPQ [Common]
⇒ PQ = PR [From (III)]
Therefore, Δ PTR ≅ Δ PUQ [By SAS-criterion of congruence]
Theorem 1: Angle-Side-Angle (ASA) Congruence rule Two triangles are congruent if two angles and the included side of one triangle are equal to two angles and the included side of the other triangle.
Given: ΔPQR and ΔMNO such that ∠PQR = ∠MNO, ∠PRQ = ∠MON and QR = NO.
To prove: Δ PQR ≅ Δ MNO.
Proof: There are three possibilities that arise.
CASE I: When PQ = MN
In this case, we have
PQ = MN
∠PQR = ∠MNO (Given)
QR = NO (Given)
Therefore, Δ PQR ≅ Δ MNO (By SAS-criterion of congruence)
CASE II: PQ < MN
Construction: Join OS such that NS = PQ.
In Δ PQR and Δ SNO, we have
PQ = SN
∠PQR = ∠MNO (Given)
QR = NO (Given)
Therefore, Δ PQR ≅ Δ SNO (By SAS-criterion of congruence)
By using corresponding parts of congruent triangles
⇒ ∠PRQ = ∠SON.
But, ∠PRQ = ∠MON. (Given)
This is possible only when ray SO coincides with ray MO or S coincides with M. Therefore, PQ must be equal to MN.
∴ ∠SON = ∠MON.
Thus, in Δ PQR and Δ MNO, we have
PQ = MN
⇒ ∠PQR = ∠MNO (Given)
⇒QR = NO (Given)
Therefore, Δ PQR ≅ Δ MNO (By SAS-criterion of congruence)
CASE III: PQ > MN.
Construction: Join SO such that NS = PQ.
In Δ PQR and Δ SNO, we have
PQ = SN
∠PQR = ∠MNO (Given)
QR = NO (Given)
Therefore, Δ PQR ≅ Δ SNO (By SAS-criterion of congruence)
By using corresponding parts of congruent triangles
⇒ ∠PRQ = ∠SON.
But, ∠PRQ = ∠MON. (Given)
This is possible only when ray SO coincides with ray MO or S coincides with M. Therefore, PQ must be equal to MN.
∴ ∠SON = ∠MON.
Thus, in Δ PQR and Δ MNO, we have
PQ = MN
⇒ ∠PQR = ∠MNO (Given)
⇒ QR = NO (Given)
Therefore, Δ PQR ≅ Δ MNO (By SAS-criterion of congruence
Hence, in all the three cases, we have Δ PQR ≅ Δ MNO.
Example 4: Check whether ∆ABC ≅ ∆PQR?
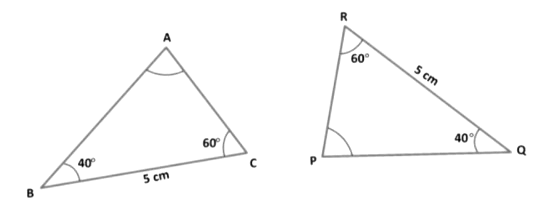
Solution: In ∆ABC and ∆PQR, we have
∠ABC = ∠PQR = 40° (Given)
BC = QR = 5 cm (Given)
∠BCA = ∠QRP = 60° (Given)
Therefore, ∆ ABC ≅ ∆ PQR (By ASA-criterion of congruence)
Example 5: In the figure, ST ∥ QP and R is the mid-points of SQ, proving that R is also the mid-point of PT.

Given: ST ∥ QP and R is the mid-point of SQ.
To prove: PR = RT.
Proof: Since QP ∥ ST and transversal PT cuts them at P and T respectively.
∴ ∠RTS = ∠RPQ. (Alternate interior angles) .........
(I) Similarly, ∠RST = ∠RQP. (Alternate interior angles) .........
(II) Since PT and SQ intersect at R.
∴ ∠QRP = ∠SRT. (Vertically opposite angles) ...........
(III) Thus, in Δ PQR and Δ SRT, we have
∠ PQR = ∠ RST [From (II)]
⇒ QR = RS [Given]
⇒ ∠ QRP = ∠ SRT [From (III)]
Therefore, Δ PQR ≅ Δ SRT [By ASA-criterion of congruence]
By using corresponding parts of congruent triangle.
⇒ PR = RT.
Hence, R is the mid-point of PT.
Some Properties of a Triangle
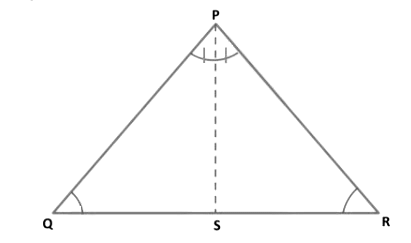
Theorem 2: Angles opposite to equal sides of an isosceles triangle are equal.
Given: ∆PQR is an isosceles triangle in which PQ = PR.To prove: ∠ PQS = ∠PRS.
Construction: Draw the bisector PS of ∠QPR which meets QR in S.
Proof: In ∆ PQS and ∆ PRS, we have
PQ = PR (Given)
⇒ ∠ QPS = ∠ RPS (By construction)
⇒ PS = PS (Common)
Therefore, ΔPQS ≅ ΔPRS (By SAS-criterion of congruence)
By using corresponding parts of congruent triangles
⇒ ∠PQS = ∠PRS.
Example 6: In Δ PQR, ∠ QPR = 80° and PQ = PR. Find ∠RQP and ∠PRQ.
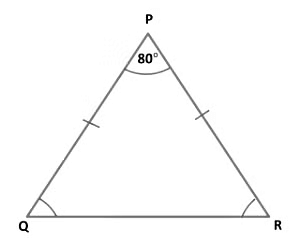
Given that: ∠QPR = 80° and PQ = PR.
Solution: We have
PQ = PR
Since angles opposite to equal sides are equal.
⇒ ∠RQP = ∠PRQ
In Δ PQR, We have
∠QPR + ∠RQP + ∠PRQ = 180°.
⇒ ∠QPR + ∠RQP + ∠RQP = 180°. (∵ ∠ RQP = ∠PRQ)
⇒ 80° + 2 ∠RQP = 180°
⇒ 2 ∠RQP = 180° - 80°
⇒ 2 ∠RQP = 100°
⇒ ∠RQP = 100°/2
⇒ ∠RQP = 50°
Hence, ∠RQP = ∠PRQ = 50°
Example 7: In figure, PQ = PR and ∠PRS = 110°. Find ∠P.
Solution: We have,
PQ = PR
Since angles opposite to equal sides are equal.
⇒ ∠PQR = ∠PRQ.
Now, ∠PRQ + ∠PRS = 180° (∵ Linear pair of angles)
⇒ ∠PRQ+ 110° = 180°
⇒ ∠PRQ = 180° - 110°
⇒ ∠PRQ = 70°
And also, ∠PQR = 70°.
Now, ∠QPR + ∠PQR + ∠PRQ = 180°
⇒ ∠QPR+ 70° + 70° = 180° (∵ ∠PQR = ∠PRQ)
⇒ ∠QPR + 140° = 180°
⇒ ∠QPR = 180°- 140°
⇒ ∠QPR = 40°.
Theorem 3: The sides opposite to equal angles of a triangle are equal.
Given: In triangle PQR, ∠PQR = ∠PRQ.
To prove: PQ = PR.
Construction: Draw the bisector of ∠QPR and let it meet QR at S.
Proof: In ∆ PQS and ∆ PRS, we have
∠PQR = ∠PRQ (Given)
⇒ ∠QPS = ∠RPS (By construction)
⇒ PS = PS (Common)
Therefore, ΔPQS ≅ ΔPRS ( By AAS-criterion of congruence)
By using corresponding parts of congruent triangles
⇒ PQ = PR.
Example 8: Check whether two triangles ABC and PQR are congruent.
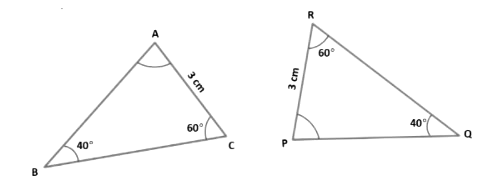
Solution: In ∆ ABC and ∆ PQR, we have
∠ABC = ∠PQR = 40o (Given)
∠BCA = ∠QRP = 60o (Given)
AC = PR = 3 cm (Given)
Therefore, ∆ ABC ≅ ∆ PQR (By AAS-criterion of congruence)
Example 9: PQ and RS are perpendiculars of equal length, to a line segment PS. Show that QR bisects PS.
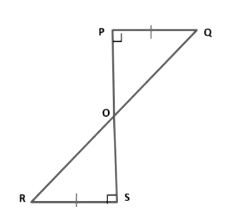
Given: PQ = RS, PQ ⊥ PS and RS ⊥ PS.
To prove: OP = OS.
Proof: In triangles OPQ and ORS, we have
∠POQ = ∠SOR [Vertically opposite angles]
∠OPQ = ∠OSR [Each equal to 90°]
PQ = RS [Given]
Therefore, Δ POQ ≅ ΔSOR [By AAS-criterion of congruence]
By using corresponding parts of congruent triangles
⇒ OP = OS.
Hence, O is the mid-point of PS.
Some More Criteria for Congruence of Triangles
Theorem 4: Side-Side-Side (SSS) Congruence rule If three sides of one triangle are equal to the three sides of another triangle, then the two triangles are congruent.
Given that: Two Δ ABC and Δ DEF such that AB = DE, BC = EF and AC = DF.
To prove: Δ ABC ≅ Δ DEF.
Construction: Suppose BC is the longest side. Draw EG such that
∠ FEG = ∠ ABC and EG = AB. Join GF and GD
Proof: In ΔABC and ΔGEF, we have
BC = EF [Given]
AB = GE [By Construction]
∠ABC = ∠GEF [By Construction]
Therefore, Δ ABC ≅ Δ GEF [By SAS-criterion of congruence]
By using corresponding parts of congruent triangles
⇒ ∠BAC = ∠EGF and AC = GF
Now, AB = DE and AB = GE
⇒ DE = GE .................. (I)
Similarly, AC = DF and AC = GF
⇒ DF = GF .................. (II)
In Δ EGD, we have
DE = GE [From (I)]
Since angles opposite to equal sides of an isosceles triangle are equal.
⇒ ∠EDG = ∠EGD ................ (III)
In Δ FGD, we have
DF = GF [From (II)]
Since angles opposite to equal sides of an isosceles triangle are equal.
⇒ ∠FDG = ∠FGD ................ (IV)
From (III) and (IV), we have,
∠EDG + ∠FDG = ∠EGD + ∠FGD
⇒ ∠EDF = ∠EGF
But, ∠BAC = ∠EDF ................. (V)
In Δ ABC and Δ DEF, we have
AC = DF [Given]
⇒ ∠BAC = ∠EDF [From (V)]
And, AB = DE [Given]
Therefore, ΔABC ≅ ΔDEF [By SAS-criterion of congruence]
Example 10: Check whether two triangles ABC and PQR are congruent.

Solution: In ∆ ABC and ∆ PQR, we have
BC = QR (Given)
⇒ AB = PQ (Given)
⇒ AC = PR (Given)
Therefore, ∆ ABC ≅ ∆ PQR (By SSS-criterion of congruence)
Example 11: In the figure, it is given that PR = QS and PS = RQ. Prove that Δ SPR ≅ Δ RQS.
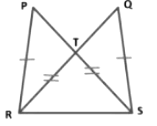
Proof: In triangles SPR and RQS, we have
PR = QS [Given]
⇒ PS = QR [Given]
⇒ RS = SR [Given]
Therefore, Δ SPR ≅ ΔRQS [By SSS-criterion of congruence]
Theorem 5: Right angle -Hypotenuse-Side (RHS) Congruence rule If in two right triangles the hypotenuse and one side of one triangle are equal to the hypotenuse and one side of the other triangle, then the two triangles are congruent.
Proof:
Consider two right triangles, △ABC and △PQR, where:
- ∠B=∠Q=90∘ (Both triangles are right-angled)
- AC is the hypotenuse of △ABC
- PR is the hypotenuse of △PQR
- AB=PQ (One side is equal)
- AC=PR (Hypotenuse is equal)
The triangles ABC and PQR both have right angles at B and Q, respectively.
The hypotenuses AC and PR are given to be equal.
The sides AB and PQ are also given to be equal.Using the RHS Congruence Rule:
Since AB=PQ, and AC=PR, and both ∠B and ∠Q are right angles, the two triangles must be congruent by the RHS criterion.
Therefore, △ABC≅△PQR.
Example 12: In the figure, two right triangles △PQR and △SUT are given such that ∠PQR=∠SUT=90∘, PR=ST, and QR=UT. If SU is extended to V such that UV=PQ and VT is joined, prove that △PQR≅△SUT and show that VT=ST.
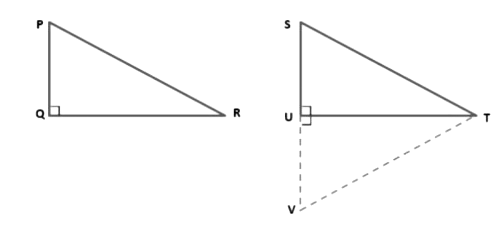
Given that: Two right triangles PQR and SUT in which ∠PQR = ∠SU = 90°, PR = ST, QR = UT.
To prove: ΔPQR ≅ ΔSUT.
Construction: Produce SU to V so that UV = PQ. Join VT.
Proof: In Δ PQR and Δ SUT, we have
PQ = VU [By construction]
∠PQR = ∠VUT [Each equal to 90°]
QR = UT [Given]
Therefore, ΔPQR ≅ ΔSUT [By SAS-criterion of congruence]
By using corresponding parts of congruent triangles
⇒ ∠QPR = ∠UVT .............. (I)
And, PR = VT
⇒ PR = ST ............ (II)
∴ VT = ST
Since, angles opposite to equal sides in Δ STV are equal.
⇒ ∠UST = ∠TVS ............. (III)
From (I) and (III), we get,
∠QPR = ∠UST .............. (IV)
And given that, ∠RQP = ∠TUS .............. (V)
Adding (IV) & (V), we get,
∠QPR + ∠RQP = ∠UST + ∠TUS ............. (VI)
∵ ∠PRQ + ∠RQP + ∠QPR = 180°
∴ ∠QPR + ∠RQP = 180 - ∠PRQ ........... (VII)
Similarly, ∠UST + ∠TUS = 180° - ∠STU ............ (VIII)
From equation (VI), (VII) & (VIII), we have
180° - ∠PRQ = 180° - ∠STU
⇒ ∠PRQ= ∠STU. ............. (IX)
Now, in Δ PQR and Δ SUT
QR = UT [Given]
⇒ ∠PRQ = ∠STU. [From (IX)]
And, PR = ST [Given]
Therefore, ΔPQR ≅ ΔSUT [By SAS-criterion of congruence]
Example 13: Check whether two triangles ABC and PQR are congruent.

Solution: In ∆ ABC and ∆ PQR, we have
∠ ABC = ∠ PQR = 90° (Given)
AC = PR (Given)
AB = PQ (Given)
Therefore, ∆ ABC ≅ ∆ PQR (By RHS-criterion of congruence)
Example 14: In the figure below, it is given that LM = MN, BM = MC, ML ⊥ AB and MN ⊥ AC. Prove that AB = AC.
 Proof: In right-angled Δ BLM and Δ CNM, we have
Proof: In right-angled Δ BLM and Δ CNM, we have
BM = MC [Given]
⇒ LM = MN [Given]
Therefore, Δ BLM ≅ Δ CNM [By RHS-criterion of congruence]
By using corresponding parts of congruent triangles
⇒ ∠LBM = ∠NCM
Since, sides opposite to equal angles are equal.
Therefore, AB = AC.
Some more Rules
1. Angle-Angle-Angle (AAA) Rule
In ΔABC and ΔPQR, we have
∠BAC = ∠QPR (Given)
∠ACB = ∠PRQ (Given)
∠CBA = ∠RQP (Given)
But, Δ ABC and Δ PQR are similar but not congruent because their sizes are different.
2. Angle-Side-Side (ASS or SSA) Rule
We have a triangle ABD. We draw AC such that AC = AD.
Now, consider the two triangles, Δ ABD and Δ ABCNow, let us check whether we can use ASS criteria for the congruency of two triangles or not. In
Δ ABD and Δ ABC, we have
∠ABD = ∠ABC (Given)
AB = AB (Common)
AD = AC (Given)
So, the corresponding Angle-Side-Side of the two triangles are equal but, these two figures are different in shape.
So, we can conclude that this method is not a universal method for proving triangles congruent.
Rules for Triangles:
For an in-depth explanation of the properties of the triangle, watch the video below:
|
44 videos|412 docs|54 tests
|
FAQs on Triangles Class 9 Notes Maths Chapter 6
| 1. How do you determine if two triangles are congruent? |  |
| 2. What are the criteria for congruence of triangles? |  |
| 3. Can two triangles be congruent if only their angles are equal? |  |
| 4. How can congruence of triangles be proven in geometric proofs? |  |
| 5. Why is it important to know when triangles are congruent? |  |

|
Explore Courses for Class 9 exam
|

|