Linear Equations in Two Variables Class 9 Notes Maths Chapter 4
| Table of contents |

|
| Introduction |

|
| Linear Equations |

|
| Solution of a Linear Equation |

|
| Conclusion |

|
Introduction
- We know that a linear equation in one variable x is an equation in the form of ax + b = 0, where a, b are real numbers such that a ≠ 0.
- The value of the variable which satisfies a given linear equation is known as its solution.
- The solution of a linear equation is also known as its root.
- If ax – b = 0 is a linear equation, then x = b/a is its solution or root.
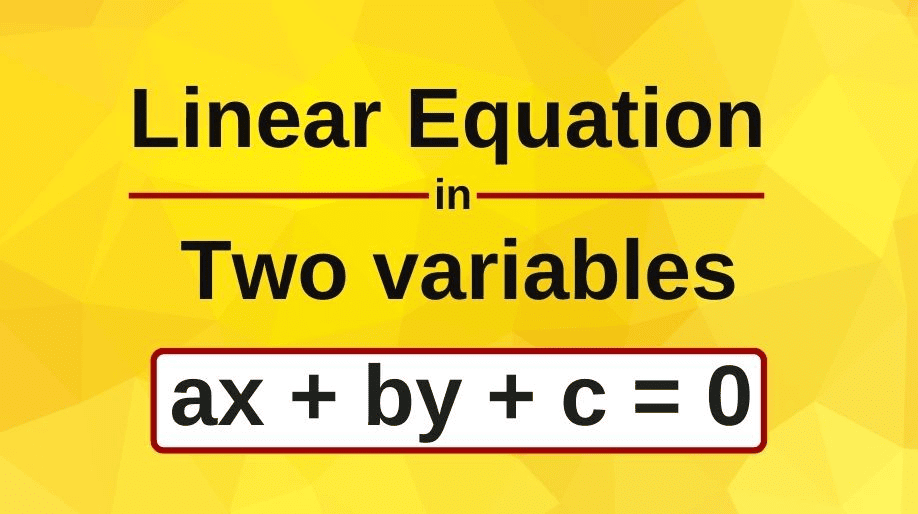 The linear equation in one variable has a unique solution. Also, it gives a straight line when plotted on a graph.
The linear equation in one variable has a unique solution. Also, it gives a straight line when plotted on a graph.
Let us consider a simple example of a linear equation in one variable
(i) 2x = 8
Here, x = 8/2 = 4 (Unique solution)
If we plot the solution of this equation on the graph we get a straight line.
 In this chapter, we recall our previous knowledge and extend it to that of the linear equation in two variables.
In this chapter, we recall our previous knowledge and extend it to that of the linear equation in two variables.
Linear Equations
An equation in which the maximum power of the variable is one is called a linear equation.
Example: x – 2 = 5, x + y = 15 and 3x – 3y = 5 are some linear equations.
Linear equations can be used to solve real-life problems such as
(i) To know the cost of five pencils if the cost of one pencil is known.
(ii) Weather predictions
(iii) To express cricket score
(iv) To know how many chocolates and balloons we can buy for the money we have
(v) Government surveys.
(1) Linear Equation in one variable
The equation of the form ax + b = 0, where a and b are real numbers such that a ≠ 0 and x is a variable, is called a linear equation in one variable.
Example:
(i) 3x + 3 = 12,
(ii) t + 2t = 7 – t
(2) Linear Equation in two variables
An equation of the form ax + by + c = 0, where a, b and c are real numbers, such that, (a and b are not both zero), and x and y are the two variables, is called as a linear equation in two variables.
Example:
(i) 3x + 2y − 5 = 0,
(ii) x − 4 = √3y
Let us consider another example of linear equation in two variables,
One day, Richa and Pranita went to Mango orchard. They both started collecting mangoes, after two hours they got tired and sat under a tree. After some time they started counting the number of mangoes collected and found that they have collected 79 mangoes in 2 hours. If we have to represent a situation in the form of an equation it is written as
x + y = 79
Here,
x: Number of mangoes collected by Richa
y: Number of mangoes collected by Pranita
We don’t know how many mangoes are collected by each one of them i.e., there are two unknown quantities. Hence, we used x and y to denote them.
So, x + y = 79
This is the required equation.
The solution of a linear equation is not affected when:
(i) The same number is added (or subtracted) from both sides of the equation.
Example: (i) 4 + 2 = 2 × 3
When we subtract 5 from both sides of the given equation we get;
(4 + 2) − 5 = (2 × 3) − 5
6 − 5 = 6 − 5
1 = 1
LHS = RHS
Hence, we can conclude that the solution of a linear equation is not affected when the same number is subtracted from both sides of the equation.
Example: (ii) 4 + 2 = 2 × 3
Added 5 to both sides of given equation and we get;
(4 + 2) + 5 = (2 × 3) + 5
6 + 5 = 6 + 5
11 = 11
LHS = RHS
Hence, we can conclude that the solution of a linear equation is not affected when the same number is added to both sides of the equation.
(ii) The same non-zero number is multiplied or divided both sides of the equation.
Example: (i) 4 + 2 = 9 − 3
Multiplied by 5 to the both sides of given equation and we get; (4 + 2) × 5 = (9 − 3) × 5
⇒ 6 × 5 = 6 × 5
30 = 30
LHS = RHS
Hence, we can conclude that the solution of a linear equation is not affected when we multiply both sides of the equation by the same non-zero number.
Example: (ii) 4 + 2 = 9 − 3
Divide by 3 to both sides of the given equation and we get;
(4 + 2) / 3 = (9 - 3) / 3
(6) / 3 = (6) / 3
2 = 2
LHS = RHS
Hence, we can conclude that the solution of a linear equation is not affected when we divide both sides of the equation by the same non- zero number.
Let’s solve some examples on Linear equations:
Example: Write each of the following equations in the form ax + by + c = 0 and indicate the values of a, b and c in each case.
(i) 3x + 4y = 7,
(ii) 2x – 8 = √3y,
(i) 3x + 4y = 7
The above equation can be re-written as
3x + 4y − 7 = 0
On comparing with ax + by + c = 0, we get
a = 3, b = 4, and c = −7
(ii) 2x – 8 = √3y
The above equation can be re-written as
2x – √3y − 8 = 0
On comparing with ax + by + c = 0, we get
a = 2, b = −√3, , and c = − 8
Example: Write each of the following as an equation in two variables x and y
(i) x = −5
(ii) 7y = 2
(i) x = −5
x + 5 = 0
1 x + 0 y + 5 = 0
(ii) 7y = 2
7y – 2 = 0
0x + 7y – 2 = 0
Example: The cost of one book is thrice the cost of a pencil. Write the linear equation in two variables to represent this statement.
Let the cost of a book be Rs. x and that of a pen to be Rs.y.
Then according to the given statement, we have
x = 3y
[OR]
1x – 3y + 0 = 0
Example: The bus fare is as follows: For the first kilometre the fare is Rs. 6 and for the subsequent distance it is Rs. 4 per km. Taking the distance covered as m km and total
fare is Rs. n. Write a linear equation for this information.
Total distance covered = m km
Fare for the first km = 6 Rs.
Fare for rest of the distance = Rs. (m - 1)4
We already know the total fare given is n
Total fare = [6 + (m - 1)4]
n = 6 + 4m – 4
n = 4m + 6 - 4
n = 4m + 2
4m – n + 2 = 0
This is the linear equation for this information.
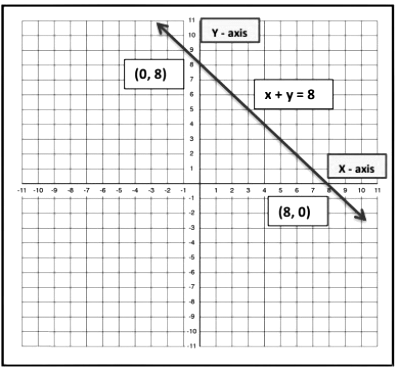
Example: John and Jimmi are two friends they are studying in class 9. Together they contributed 8 dollars for flood victims. Write a linear equation that satisfies the given data. Also, draw a graph for that.
Let the amount that John and Jimmi contributed to be x and y respectively.
Amount contributed by John + Amount contributed by Jimmi = 8.So, x + y = 8
This is a linear equation that satisfies the data.
To draw a graph we need to find a x and y co-ordinate which satisfy the equation
x + y = 8 ..........(1)
Put y = 0 in the equation (1)
x + 0 = 8
x = 8
x + y = 8..........(1)
Put x = 0 in the equation (1)
0 + y = 8
y = 8
So, it can be observed that (8, 0), (0, 8) satisfy the equation 1.
Therefore these are the solution of the above equation.
The graph is constructed as follow:
Solution of a Linear Equation
“The values of variable involved in a linear equation which satisfy the equation i.e., the equation of LHS and RHS are equal, is called the solution of the linear equation.”
1. Solution of Linear Equations in One Variable
“Any value of the variable that satisfies the given equation in x is called a solution or roots of the equation. We know the Linear equation in one variable has a unique solution.
Example:
(i) 3x + 3 = 12
3x = 12 – 3
3x = 9
x = 9/3
x = 3 is a solution of the given equation, which is unique.
(ii) 2x – 7 = 0
i. e. , 2x = 7
x = 7/2 is a solution of the given equation, which is unique.
2. Solution of Linear Equations in two Variables
There are two variables in the equation, a solution means a pair of values, one for x and one for y which satisfy the given equation. A linear equation in two variables has infinitely many solutions.
Example: x + 3y = 5
LHS = x + 3y
If we put x = 2 and y = 1 in the LHS of the equation we get,
LHS = x + 2y = 3 + 3(1) = 5
Here, LHS = RHS
So, we can say that x = 2 and y = 1 is a solution of the equation x + 3y = 5
Let us consider one more value of x and y.
Putting x = 1 and y = 2 in the LHS of the equation we get,
LHS = x + 3y
LHS = x + 3y = 1 + 3(2) = 7
Now, LHS ≠ RHS
Therefore, we can say that x = 1 and y = 2 is not a solution of the equation x + 3y = 5.
Write Find the value of k in the following case, if x = 2, y = 1 is a solution of the equations:
(i) 3x + 2y = k
Put x = 2, y = 1,then
3(2) + 2(1) = k
6 + 2 = k
k = 8
(ii) x4 + y3 = 5k
Put x = 2, y = 1, then
24 + 13 = 5k
2 × 3 + 1 × 44 × 3 = 5k
6 + 412 = 5k
1012 = 5k
56 = 5k
5k1 = 56
k = 16
Conclusion
- A linear equation in two variables is an equation that can be written in the form ax + by + c = 0, where a, b, and c are real numbers, and a and b are not both zero.
- A linear equation in two variables does not have just one solution, but infinitely many solutions. This is because there are countless combinations of x and y values that can satisfy the equation.
- Every point that lies on the graph of a linear equation in two variables is a solution to that equation. Conversely, every solution of the equation corresponds to a point on its graph. This means that the graph visually represents all possible solutions to the equation.
|
40 videos|471 docs|57 tests
|
FAQs on Linear Equations in Two Variables Class 9 Notes Maths Chapter 4
| 1. What is a linear equation in two variables? |  |
| 2. How can we find the solution of a linear equation in two variables? |  |
| 3. What is the graphical representation of linear equations in two variables? |  |
| 4. What are some real-life applications of linear equations in two variables? |  |
| 5. Can a linear equation in two variables have multiple solutions? |  |