Properties of Numbers: Even & Odd | Quantitative for GMAT PDF Download
| Table of contents |

|
| Even Numbers |

|
| Odd Numbers |

|
| Consecutive Integers |

|
| Even and Odd Number Properties |

|
| Arithmetic Rules of Odds & Evens |

|
| Other Important Properties of Numbers |

|
Even and odd numbers are two categories of integers, which are whole numbers and their negatives, including zero. Understanding the characteristics of even and odd numbers is fundamental in mathematics.
Even Numbers
- Even numbers are integers that are divisible by 2. In other words, when an even number is divided by 2, the result is a whole number with no remainder.
- Examples of Even Numbers: 0, 2, 4, 6, 8, 10, 12, and so on.
- Characteristics:
~ All even numbers end in 0, 2, 4, 6, or 8.
~ Consecutive even numbers increase by 2 (e.g., 2, 4, 6).
Odd Numbers
- Odd numbers are integers that are not divisible by 2. When an odd number is divided by 2, the result is a quotient with a remainder of 1.
- Examples of Odd Numbers: 1, 3, 5, 7, 9, 11, and so on.
- Characteristics:
~ All odd numbers end in 1, 3, 5, 7, or 9.
~ Consecutive odd numbers also increase by 2 (e.g., 3, 5, 7).
Consecutive Integers
- Consecutive integers alternate between even and odd. For example, the sequence 9, 10, 11, 12, 13... follows the pattern: Odd, Even, Odd, Even, Odd.
- This alternation occurs because adding 1 to an even number results in an odd number, and adding 2 to an odd number results in the next even number.
- Negative Integers:
Even and odd classifications also apply to negative integers.
Examples of Negative Even Numbers: -2, -4, -6, -8, -10, -12, and so on.
Examples of Negative Odd Numbers: -1, -3, -5, -7, -9, -11, and so on.
The same rules for divisibility by 2 apply to negative numbers.
Even and Odd Number Properties
Now that we know what are even and odd numbers, let’s see their properties.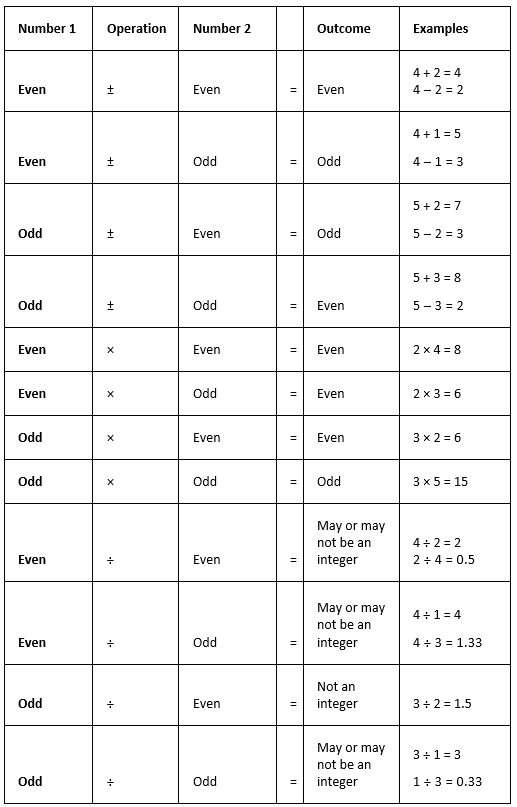
Arithmetic Rules of Odds & Evens
1. Addition and Subtraction:
- When you add or subtract two even integers or two odd integers, the outcome is always an even integer.
- For instance, 7 + 11 = 18 and 8 + 6 = 14 both result in even numbers. On the other hand, combining an odd integer with an even integer in either addition or subtraction will always yield an odd integer.
For example, 7 + 8 = 15.
2. Multiplication:
- When multiplying integers, the resulting product is even if at least one of the integers is even. Conversely, if all the integers being multiplied are odd, the result is odd. For instance, consider the multiplication of 3, 8, 9, and 13: 3 x 8 x 9 x 13 = 2,808, which is even.
- Moreover, the multiplication of several even integers leads to a product that is divisible by higher powers of 2. For instance, if two even integers are multiplied, the result is divisible by 4 (e.g., 2 x 5 x 6 = 60). If three even integers are multiplied, the result is divisible by 8 (e.g., 2 x 5 x 6 x 10 = 600).
Odd ± Even = Odd
Odd x Odd = Odd
Odd + Odd = Even
Even x Even = Even (and divisible by 4)
Even ± Even = Even
Odd x Even = Even
3. Division:
- Division of integers does not guarantee specific outcomes, as the result may not be an integer. Various outcomes are possible, depending on the values of the dividend and divisor.
4. Examples:
- Addition/Subtraction:
9+9+3=12 (Even)
15−7=815−7=8 (Even)
5+6=115+6=11 (Odd)
10−4=610−4=6 (Even) - Multiplication:
4×7×9= 252 (Even)
3×5×11165 (Odd) - Division:
14÷7=2 (Even)
9÷4=2.25 (Not an integer)
Other Important Properties of Numbers
1. Properties Prime Numbers
A number which is divisible by only two number, 1 and the number itself, is called a prime number.
Example: 2, 3, 5, 7, 11……….
Note: 2 is the only prime number, which is even, because all other even numbers will be divisible by at least three numbers, 1, 2 and the number itself.
Every positive integer can be expressed as a product of one or more prime numbers
Example: 55 = 5 * 11, where 5 and 11 are two prime numbers
Based on the above definition, Is 1 a prime number?
So, we know what is a prime number, but how do we check whether a given number is prime or not?
What is the process to check whether a given number is prime or not?
It is easy to check whether a single-digit or a two-digit number is prime or not, but what if we are given a three-digit number or more.
- Let’s say the number is 123, can we quickly find whether 123 is prime or not?
For this, let us learn a five-step approach to check whether a given number is a prime number or not?
Step 1: Find the square root of the given number
- The square root of 123 approximately equal to 11 as 112 = 121
Step 2: Round it off to the closest integer
- The closest integer is 11.
Step 3: List down all the prime numbers which are less or equal to this integer
- Prime numbers less than or equal to 11 are 2, 3, 5, 7, and 11.
Step 4: Check whether any of these prime numbers can divide the given number or not
- 123 is not divisible by 2.
- But 123 is divisible by 3.
- We need not check for other prime numbers
Step 5: If yes then the given number is not a prime number, else it is a prime number
- 123 is divisible by 3. Hence, it is not a prime number.
Prime Factorization
We already know that any given positive integer can be expressed as a product of one or more prime numbers. This representation of any number is called prime factorization.
For example: 420 = 2 × 210 = 2 × 2 × 105 = 2 × 2 × 3 × 35 = 2 × 2 × 3 × 5 × 7 = 22 × 3 × 5 × 7
Now, let us learn a few more properties of numbers where we apply prime factorization.
2. Properties of Least Common Multiple (LCM)
Before we see what an LCM is, let us understand the meaning of a multiple.
Multiple: If the remainder when a number “N” is divided by another number “n” is zero, then N is said to be a multiple of n.
And, LCM is the smallest common multiple of any two or more given positive integers.
For example: LCM of 4 and 6 is 12, since 12 is the smallest number, which is a multiple of both 4 and 6
3. Properties of Highest Common Factor or Greatest Common Divisor (HCF/GCD)
Let us first learn what is a factor or divisor, and then we can learn about GCD or HCF.
Factor/Divisor: If the remainder when a number “N” is divided by another number “n” is zero, then n is said to be a factor or divisor of N.
And, HCF or GCD is the largest common factor/divisor to any two or more given positive integers.
For example: The GCD of 24 and 30 is 6, since 6 is the greatest number, which is a factor of both 24 and 30.
Solved Examples
Question 1: What is the even/odd nature of the expression, 2k2 + 14k + 7, where k is a positive integer?
1. Even
2. Odd
3. Cannot be determined
Solution:
Given
- An expression, 2k2 + 14k + 7, where k is a positive integer
To find
- The even/odd nature of the given expression
Approach and Working out
- We can write, 2k2 + 14k + 7 = 2k2 + 14k + 6 + 1
Now, if we see, in the given expression
- The term 2k2 is always even, for any value of k
- Since, even * any integer = even
- The term 14k is always even, for any value of k
- Since, even * any integer = even
- The term 6 is also even, and 1 is odd
So, 2k2 + 14k + 7 = 2k2 + 14k + 6 + 1 = even + even + even + odd = odd
Therefore, the given expression is always odd, for any value of k
Hence, the correct answer is Option B.
Question 2: The LCM of two positive integers, p, and q, is 42 and HCF is 1. If p is an even prime number, then what is the value of q?
1. 6
2. 7
3. 14
4. 21
5. 42
Solution: Given
- Two positive integers, p, and q
- p is an even prime number
- LCM pf p and q = 42
- HCF of p and q = 1
To find
- The value of q
Approach and Working out
The value of p = 2, since 2 is the only even prime number
And, we know that,
- LCM × HCF = the product of the two integers
- 42 × 1 = 2 × q
Therefore, the value of q = 42/2 = 21.
Hence, the correct answer is Option D.
|
115 videos|106 docs|113 tests
|
FAQs on Properties of Numbers: Even & Odd - Quantitative for GMAT
| 1. What are even numbers? |  |
| 2. What are odd numbers? |  |
| 3. What are consecutive integers? |  |
| 4. What are the properties of even numbers? |  |
| 5. What are the properties of odd numbers? |  |

|
Explore Courses for GMAT exam
|

|


















