Percentages | Quantitative for GMAT PDF Download
The Concept of Percentages
Percent, when broken apart, literally means per one hundred. A percent represents a part of 100. For example, 20% means 20 per 100.
Fraction Representation
Since a percent is an amount per 100, percents can be represented as fractions with a denominator of 100.
25% = 25/100
55% = 55/100
100% = 100/100
125% = 125/100
250% = 250/100
0.5% = 5/1000
When a percentage is represented as a fraction, it can be added, subtracted, multiplied, and divided just like any other fraction.
Decimal Representation
A percent can be represented as a decimal. The following relationship characterizes how percentages and decimals interact.
Percent Form * (.01) = Decimal Form
Stated in sentence form: To move from percent form to decimal form, move the decimal point two slots to the left.
Consider the following examples:
What is 5% represented as a decimal?
5 * (.01) = .05
Note: .05 is the result of taking 5 and moving the decimal point two slots to the left.
What is 130% represented as a decimal?
130 * (.01) = 1.3
Note: 1.3 is the result of taking 130 and moving the decimal point two slots to the left.
What is 0.5% represented as a decimal?
0.5 * (.01) = 0.005
Note: 0.005 is the result of taking 0.5 and moving the decimal point two slots to the left.
When a percentage is represented as a decimal, it can be added, subtracted, multiplied, and divided just like any other number.
Summary
The following chart lays out the relationship between percents, fractions, and decimals.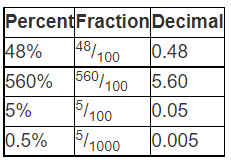
Percent Change vs. Percent of
While most students find percentages to be an easier topic than one such as combinatorics, some individuals initially trip on the difference between a percent change and a percent of a number. Practically, this is the difference between saying "the price jumped 50%" and "the current price is 150% of the old price." Both of these phrases refer to the same amount, but are stated differently.
Percent Change
Percents are commonly used to measure or report the change in an amount. For example, a news reporter might say, "stocks rose 1.5% today" or a demographer might write, "minority representation in the population fell 3.5% during the past decade." The formula for calculating percent changes is:
This formula can also be expressed in decimal form. In other words, the following formula calculates the percent change between two numbers and represents this change in decimal form.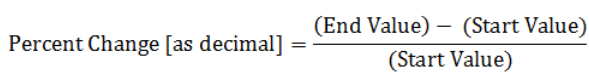
The following examples illustrate the use of this formula.
A company recently saw its stock fall from $10 to $9 as a result of a lawsuit award. What percent did the stock drop?
End Value = 9
Start Value = 10
Percent Change [as a percent] = ((9 - 10)/10) * 100 = -.1 * 100 = -10%
Another Example:
As a result of an increase in the required minimum wage and an increase in the price of raw materials, a manufacturer raised the price of its product from $50 to $60. By what percent did the manufacturer raise the price of its product?
End Value = 60
Start Value = 50
Percent Change [as a percent] = ((60 - 50)/50) * 100 = .2 * 100 = 20%
It is possible to calculate the percent change of a percent. Consider the following example:
Since the local government increased funding of high school education 10 years ago, the percent of students accepted at accredited four year universities jumped from 75% to 85%. By what percent did the percent of students accepted at four year universities increase over the 10 year period?
End Value = 85% = .85
Start Value = 75% = .75
Using Percents: Percent Change [as a percent] = ((85% - 75%)/75%) * 100 = 13.3% * 100 = 13.3%
Using Decimals: Percent Change [as a decimal] = ((.85 - .75)/.75) * 100 = .133
A Common Mistake in Working With Percent Decreases
Some students confuse a percent decrease of a certain percentage with finding the percent of a certain amount. The following example elucidates this confusion:
A foreign stock market index stood at 5,000 last year. However, since that time, its value fell 45%. What is the current value of the stock index?
Common Mistake: Index Today = 5000(.45)
This calculation yields 45% of last year's index value. However, the question pertains to a 45% fall. Since the index's value fell 45%, its current value is 100% - 45% = 55% of last year's index value.
Correct Calculation: Index Today = 5000(1-.45) = 5000(.55) = 2750
Percent of
Another common use of percents is as a measure of another number. For example, a stock analyst might say, "MicroMake's stock is trading at 130% of MacroMake's stock price." Similarly, a political historian might say, "President George W. Bush's approval rating in late November 2004 was about 50%, which is about 55% of his approval rating in late September 2001." In these instances, percents are being used not to describe change, but to compare amounts or quantities.
When working with percents that are used to compare different quantities, it is often best to translate each percent into decimals and set up equations or ratios. Consider the following examples:
What is 50% of 40?
Translate 50% into decimal format: 50% = .5
Translate the question into an equation: .5(40) = ?
.5(40) = 20
The following is a slightly more difficult example:
20 is what percent of 80?
Let X = the percent as a decimal
Translate the question into an equation: X(80) = 20
X = 20/80 = 1/4 = .25
Translate X into a percent: .25(100) = 25%
Percents can also be used to compare the size of percents. Consider the example with President George W. Bush's approval rating mentioned above.
President George W. Bush's approval rating in late November 2004 was about 50%, which is about 55% of his approval rating in late September 2001. What was President Bush's approval rating in late September 2001?
Let A = President Bush's approval rating in late September 2001
Condense Question Down to Simplify: 50% is 55% of A
Translate Into Equation: .50 = .55A
A [as a decimal] = .9
A [as a percent] = .9(100) = 90%
Recursive Percents
If a number rises by 30% and then falls by 35%, by what percent did it change from beginning to end? The topic of recursive (or successive) percents addresses this question. Consider an example:
From 2004 through 2007, the Dow Jones Industrials Average rose about 30%. However, during 2008, the Dow fell about 35%. About what percent did the Dow Jones change from 2004 through 2008?
Let DowBeginning of 2004 = X
DowEnd of 2007 = X(1 + 30%) = X(1.3)
DowEnd of 2008 = [X(1.3)](1-.35) = X(.845)
Percent Change = (End - Start/Start)*100
Percent Change = (X(.845) - X/X)*100 = -15.5%
Strategy: Picking Numbers (Especially 100)
Many students find it easier to solve problems involving percents by picking numbers instead of using theoretical variables. The previous question can be solved this way:
From 2004 through 2007, the Dow Jones Industrials Average rose about 30%. However, during 2008, the Dow fell about 35%. About what percent did the Dow Jones change from 2004 through 2008?
Let DowBeginning of 2004 = 100 [pick the number 100 instead of using a variable]
DowEnd of 2007 = 100(1.3)
DowEnd of 2008 = 100(1.3)(1-.35) = 84.5
The choice of 100 as a value for the Dow at the beginning of 2004 makes calculating the percent change from 2004 through 2008 much easier, as the next step should indicate.
Percent Change = (End - Start/Start)*100
Percent Change = (84.5 - 100/100)*100 = -15.5%
Interest Rate Problems
One rather common and important application of percents is the topic of interest rates and money. An important formula that relates interest, principal, and time follows:
Simple Interest Formula
I = PRT
I = Interest Payment
P = Principal
R = Interest Rate
T = Time Period
If a homeowner signs a 10 year loan for 5% worth $100,000, how much will his interest payment be the first year (assuming he pays interest once annually)?
T = 1 since the question asks for the interest, I, in the first year (i.e., a one year time period--not the entire 10 year time period)
P = $100,000
R = 5% = 0.05
I = $100,000(.05)(1) = $5000
While the above formula helps solve many problems, there are other problems that require another formula. The following formula is fundamental to the relationship between interest, time, present value, and future value:
FV = PV(1 + r)t
FV = Future Value = The amount of money to be received or owed at a future date t time periods from now
PV = Present Value = The amount of money to be received or owed at present (i.e., now)
r = Interest Rate = The interest rate on the money, expressed as a decimal
t = Time = The amount of time to pass between PV and FV
Note: The time period, t, and interest rate, r, must be expressed in the same terms. For example, one cannot use an annual interest rate and express time in terms of months. If you are using a value of t that expresses time in months, you must use a monthly interest rate. For more on this topic, see the compound interest section.
The following is an example of a common introductory interest rate problem.
If Sam invests $100,000 today and earned 5% a year, how much money would Sam have in 2 years?
PV = $100,000
r = 5% = 0.05
t = 2
FV = $100,000(1 + .05)2 = $110,250
|
115 videos|106 docs|113 tests
|
FAQs on Percentages - Quantitative for GMAT
| 1. What is the concept of percentages? |  |
| 2. How do I calculate percentages? |  |
| 3. What are some practical applications of percentages? |  |
| 4. How can I convert a decimal or a fraction into a percentage? |  |
| 5. What is the importance of understanding percentages in everyday life? |  |

|
Explore Courses for GMAT exam
|

|

















