Important Definitions & Formulas: Arithmetic Progressions | Elementary Mathematics for PAT PDF Download
The chapter on "Arithmetic Progression" is crucial for understanding the patterns and principles behind sequences of numbers, forming the basis for solving a wide range of mathematical problems in various fields.
This document provides Class 10 Mathematics Formulas for Arithmetic Progressions that can help you succeed in board exams and in future competitive exams.
Important Definitions and Terms
Arithmetic Progressions
An Arithmetic Progression (AP) is a sequence of numbers in which the difference between any two consecutive terms is constant. This constant is called the common difference (d).
General Form of AP:
a, a + d , a + 2d , a + 3d ,…, a + (n−1)d
where
- a = First term
- d = Common difference
- n = Number of terms
First Term of an A.P.
The AP can also be written using the common difference, as follows
a, a + d, a + 2d, a + 3d, a + 4d, ………., a + (n – 1) d
where “a” is the first term of the progression.

Example 1:
Consider an arithmetic progression with a common difference (d) of 3. If we have the following terms in the AP:
a, a + 3, a + 6, a + 9, a + 12, ...
Sol: In this case, the first term (a) is the initial value of the progression. For example, if a = 2, the first term of the AP would be 2.
Example 2:
Let's take another example of an arithmetic progression with a common difference (d) of -2. The terms of the AP are given by:
a, a - 2, a - 4, a - 6, a - 8, ...
Sol: Again, the first term (a) represents the starting value of the progression. For instance, if a = 10, the first term of the AP would be 10.
In both examples, "a" denotes the first term of the arithmetic progression.
Common Difference
In an arithmetic progression, the terms are identified by their position (first term, second term, etc.), the
common difference between consecutive terms, and the nth term. If the series is denoted by a1, a2, a3, ……………., an, then the common difference "d" can be determined by:
d = a2 – a1 = a3 – a2 = ……. = an – an – 1
Here are two examples of the common difference in an arithmetic progression (AP):
Example 1: Consider the following arithmetic progression: 3, 7, 11, 15, 19, ...
Sol: To find the common difference (d), we can take the difference between any two consecutive terms. Let's calculate:
d = 7 - 3 = 4
In this case, the common difference is 4. Each term in the progression is obtained by adding 4 to the previous term.
Example 2: Let's take another arithmetic progression: -2, -5, -8, -11, -14, ...
Sol: To determine the common difference (d), we can subtract any two consecutive terms:
d = -5 - (-2) = -3
In this example, the common difference is -3. Each term in the progression is obtained by subtracting 3 from the previous term.
In both cases, the common difference (d) represents the constant value by which consecutive terms in the arithmetic progression differ from each other.
Important Formulas
When it comes to Arithmetic Progression, there are two essential formulas that we need to know like the back of our hand:
- The nth term of AP
- Sum of the first n terms
Let’s understand both formulas with examples.
The nth Term of an AP
The formula for finding the nth term of an AP is:
| an = a + (n − 1) × d |
Example 1: Find the 12th term of an arithmetic progression with a first term of 8 and a common difference of 5.
Sol:
a12 = a1 + (n-1)d
a12 = 8 + (12-1) × 5
a12 = 8 + 55
a12 = 63
Example 2: If the 5th term of an arithmetic progression is 17 and the common difference is -3, find the first term.
Sol:
a5 = a1 + (n-1)d
17 = a1 + (5-1) × (-3)
17 = a1 - 12
a1 = 29
Sum of n Terms of AP
The formula for finding the sum of the first n terms of an arithmetic progression can be determined if you know the first term, common difference, and the number of terms. This formula helps in calculating the total sum of an AP series.
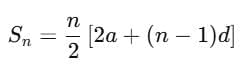 |
Sol:
To find the sum of the first 20 terms of an AP, we can use the formula:
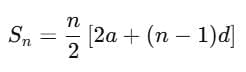
where Sn is the sum of the first n terms, a is the first term, d is the common difference, and n is the number of terms.
Substituting the given values, we get:
S20 = (20/2) x [2(3) + (20-1)(4)]
S20 = 10 x [6 + 76]
S20 = 820
Therefore, the sum of the first 20 terms of the AP is 820.
Example 2: Find the sum of the first 20 terms of an AP where the first term is 10 and the common difference is 5.
Sol:
Here, the first term (a) = 10, the common difference (d) = 5, and n (total number of terms) = 20.
Using the formula for the sum of n terms of an AP, we have:
S20 = (20/2) × [2(10) + (20 - 1)(5)]
S20 = 10 × [20 + 95]
S20 = 10 × 115
S20 = 1150
Sum of AP when the Last Term is Given
The formula to find the sum of an AP when the first and last terms are given is as follows:
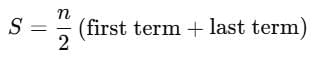 |
Example 1: Find the sum of an arithmetic progression if the last term is 35, the first term is 5, and there are 8 terms in total.
Sol:
Using the formula 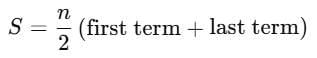 ,
,
we have: S = 8/2 (5 + 35)
S = 4 x 40
S = 160
Therefore, the sum of the given arithmetic progression is 160.
|
7 videos|256 docs|37 tests
|
FAQs on Important Definitions & Formulas: Arithmetic Progressions - Elementary Mathematics for PAT
| 1. What is an arithmetic progression (AP)? |  |
| 2. How do you find the nth term of an arithmetic progression? |  |
| 3. What is the formula for the sum of n terms in an arithmetic progression? |  |
| 4. How do you find the sum of an arithmetic progression when the last term is given? |  |
| 5. Can an arithmetic progression have negative common difference? |  |

















