Class 8 Exam > Class 8 Notes > Mathematics (Maths) Class 8 > Important Formulae: Comparing Quantities
Important Formulae: Comparing Quantities | Mathematics (Maths) Class 8 PDF Download
Terms
1. Unitary Method
Unitary method is on the most useful method to solve ratio, proportion and percentage problems. In this we first find value of one unit and then find the value of required number of units.
So in Short Unitary method comprises two following steps:
- Step 1: Find the value of one unit.
- Step 2: Then find the value of required number of units.
2. Percentages
- Percentages are ways to compare quantities. They are numerators of fractions with denominator 100 or it basically means per 100 value
- Percent is derived from Latin word ‘per centum’ meaning ‘per hundred’
It is denoted by % symbol
1% means 1/100= .01 - We can use either unitary method or we need to convert the fraction to an equivalent fraction with denominator 100
3. Discounts
- Discount is a reduction given on the Marked Price (MP) of the article.
- This is generally given to attract customers to buy goods or to promote sales of the goods.
- You can find the discount by subtracting its sale price from its marked price.
So, Discount = Marked price – Sale price
Question for Important Formulae: Comparing QuantitiesTry yourself: What is the unitary method used for?View Solution
4. Interest: Interest is the extra money paid by institutions like banks or post offices on money deposited (kept) with them. Interest is also paid by people when they borrow money.
5. Simple Interest
- Principal (P): The original sum of money loaned/deposited. Also known as capital.
- Time (T): The duration for which the money is borrowed/deposited.
- Rate of Interest (R): The percent of interest that you pay for money borrowed, or earn for money deposited.
- Simple interest is calculated as
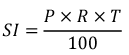
- Total amount at the end of time period
A= P + SI
6. Compound interest
- Principal (P): The original sum of money loaned/deposited.
- Time (n): The duration for which the money is borrowed/deposited.
- Rate of Interest (R): The percent of interest that you pay for money borrowed, or earn for money deposited
- Compound interest is the interest calculated on the previous year’s amount (A = P + I).
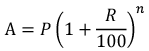
The document Important Formulae: Comparing Quantities | Mathematics (Maths) Class 8 is a part of the Class 8 Course Mathematics (Maths) Class 8.
All you need of Class 8 at this link: Class 8
|
79 videos|408 docs|31 tests
|
FAQs on Important Formulae: Comparing Quantities - Mathematics (Maths) Class 8
| 1. What is the formula for calculating the percentage increase or decrease in quantities? |  |
Ans. The formula for calculating the percentage increase is:
\[
\text{Percentage Increase} = \left( \frac{\text{New Value} - \text{Old Value}}{\text{Old Value}} \right) \times 100
\]
For percentage decrease, the formula is:
\[
\text{Percentage Decrease} = \left( \frac{\text{Old Value} - \text{New Value}}{\text{Old Value}} \right) \times 100
\]
| 2. How can I compare two quantities using the ratio method? | |
Ans. To compare two quantities using the ratio method, you divide one quantity by the other. The formula is:
\[
\text{Ratio} = \frac{\text{Quantity A}}{\text{Quantity B}}
\]
This gives you a fraction that can be simplified to show how many times one quantity is greater or lesser than the other.
| 3. What is the difference between simple interest and compound interest in the context of comparing quantities? | |
Ans. Simple interest is calculated on the principal amount throughout the entire duration, using the formula:
\[
\text{Simple Interest} = \text{Principal} \times \text{Rate} \times \text{Time}
\]
Compound interest, however, is calculated on the principal and also on the accumulated interest of previous periods, using the formula:
\[
\text{Compound Interest} = \text{Principal} \times \left(1 + \frac{\text{Rate}}{n}\right)^{n \times t} - \text{Principal}
\]
Comparing these two helps in understanding how much more can be earned with compound interest over time.
| 4. How do I convert fractions to percentages when comparing quantities? | |
Ans. To convert a fraction to a percentage, divide the numerator by the denominator and then multiply by 100. The formula is:
\[
\text{Percentage} = \left( \frac{\text{Numerator}}{\text{Denominator}} \right) \times 100
\]
For example, to convert \(\frac{3}{4}\) to a percentage:
\[
\text{Percentage} = \left( \frac{3}{4} \right) \times 100 = 75\%
\]
| 5. What are the applications of comparing quantities in real-life scenarios? | |
Ans. Comparing quantities is essential in various real-life scenarios such as budgeting, calculating discounts during sales, assessing performance metrics, and making investment decisions. By understanding how to compare quantities, one can make informed choices regarding finance, purchasing, and resource allocation.
About this Document
|
3.8K Views |
|
4.93/5 Rating |
|
Dec 22, 2024 Last updated |
Document Description: Important Formulae: Comparing Quantities for Class 8 2024 is part of Mathematics (Maths) Class 8 preparation.
The notes and questions for Important Formulae: Comparing Quantities have been prepared according to the Class 8 exam syllabus. Information about Important Formulae: Comparing Quantities covers topics
like and Important Formulae: Comparing Quantities Example, for Class 8 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Important Formulae: Comparing Quantities.
Introduction of Important Formulae: Comparing Quantities in English is available as part of our Mathematics (Maths) Class 8
for Class 8 & Important Formulae: Comparing Quantities in Hindi for Mathematics (Maths) Class 8 course.
Download more important topics related with notes, lectures and mock test series for Class 8
Exam by signing up for free. Class 8: Important Formulae: Comparing Quantities | Mathematics (Maths) Class 8
Description
Full syllabus notes, lecture & questions for Important Formulae: Comparing Quantities | Mathematics (Maths) Class 8 - Class 8 | Plus excerises question with solution to help you revise complete syllabus for Mathematics (Maths) Class 8 | Best notes, free PDF download
Information about Important Formulae: Comparing Quantities
In this doc you can find the meaning of Important Formulae: Comparing Quantities defined & explained in the simplest way possible. Besides explaining types of
Important Formulae: Comparing Quantities theory, EduRev gives you an ample number of questions to practice Important Formulae: Comparing Quantities tests, examples and also practice Class 8
tests
|
Explore Courses for Class 8 exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
Related Searches
study material
,MCQs
,Important Formulae: Comparing Quantities | Mathematics (Maths) Class 8
,Important questions
,Exam
,Previous Year Questions with Solutions
,Viva Questions
,mock tests for examination
,Extra Questions
,Important Formulae: Comparing Quantities | Mathematics (Maths) Class 8
,Free
,past year papers
,video lectures
,Objective type Questions
,ppt
,practice quizzes
,shortcuts and tricks
,Semester Notes
,Summary
,Sample Paper
,Important Formulae: Comparing Quantities | Mathematics (Maths) Class 8
;
Additional Information about Important Formulae: Comparing Quantities for Class 8 Preparation
Important Formulae: Comparing Quantities Free PDF Download
The Important Formulae: Comparing Quantities is an invaluable resource that delves deep into the core of the Class 8 exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Important Formulae: Comparing Quantities now and kickstart your journey towards success in the Class 8 exam.
Importance of Important Formulae: Comparing Quantities
The importance of Important Formulae: Comparing Quantities cannot be overstated, especially for Class 8 aspirants.
This document holds the key to success in the Class 8 exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Important Formulae: Comparing Quantities Notes
Important Formulae: Comparing Quantities Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Important Formulae: Comparing Quantities.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Important Formulae: Comparing Quantities Notes on EduRev are your ultimate resource for success.
Important Formulae: Comparing Quantities Class 8 Questions
The "Important Formulae: Comparing Quantities Class 8 Questions" guide is a valuable resource for all aspiring students preparing for the
Class 8 exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Important Formulae: Comparing Quantities on the App
Students of Class 8 can study Important Formulae: Comparing Quantities alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Important Formulae: Comparing Quantities,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Important Formulae: Comparing Quantities is prepared as per the latest Class 8 syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup