Class 9 Exam > Class 9 Notes > Mathematics (Maths) Class 9 > Important Formulas: Heron's Formula
Important Formulas: Heron's Formula | Mathematics (Maths) Class 9 PDF Download
Important Formulas
Unit Conversion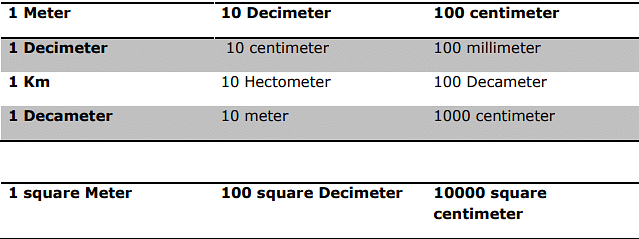

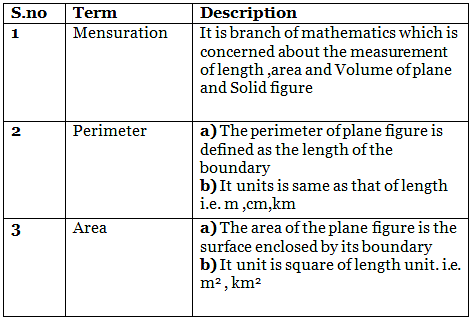
Perimeter and Area of Different Figure
The document Important Formulas: Heron's Formula | Mathematics (Maths) Class 9 is a part of the Class 9 Course Mathematics (Maths) Class 9.
All you need of Class 9 at this link: Class 9
|
44 videos|412 docs|54 tests
|
FAQs on Important Formulas: Heron's Formula - Mathematics (Maths) Class 9
| 1. What is Heron's Formula and how is it used to calculate the area of a triangle? |  |
Ans.Heron's Formula is a mathematical formula that allows you to calculate the area of a triangle when you know the lengths of all three sides. If a triangle has sides of lengths \(a\), \(b\), and \(c\), the semi-perimeter \(s\) is calculated as \(s = \frac{a + b + c}{2}\). The area \(A\) can then be found using the formula: \(A = \sqrt{s(s-a)(s-b)(s-c)}\).
| 2. Can Heron's Formula be applied to any type of triangle? |  |
Ans.Yes, Heron's Formula can be applied to any type of triangle, whether it is scalene, isosceles, or equilateral, as long as the lengths of all three sides are known.
| 3. How do you find the semi-perimeter using Heron's Formula? |  |
Ans.The semi-perimeter \(s\) of a triangle is found by adding the lengths of the three sides and dividing by 2. Mathematically, it is expressed as \(s = \frac{a + b + c}{2}\), where \(a\), \(b\), and \(c\) are the lengths of the sides of the triangle.
| 4. What are the steps to use Heron's Formula to find the area of a triangle? |  |
Ans.To use Heron's Formula to find the area of a triangle, follow these steps:
1. Determine the lengths of the three sides \(a\), \(b\), and \(c\).
2. Calculate the semi-perimeter \(s = \frac{a + b + c}{2}\).
3. Use Heron's Formula \(A = \sqrt{s(s-a)(s-b)(s-c)}\) to compute the area.
| 5. Are there any limitations to using Heron's Formula? |  |
Ans.Heron's Formula requires that the triangle must exist, which means the lengths of the sides must satisfy the triangle inequality theorem. If the sum of the lengths of any two sides is less than or equal to the length of the third side, the triangle cannot be formed, and Heron's Formula cannot be applied.

|
Explore Courses for Class 9 exam
|

|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
Related Searches


















