Heron’s Formula Class 9 Notes Maths Chapter 10
| Table of contents |

|
| Introduction |

|
| Area of a Triangle — by Heron’s Formula |

|
| Verification and Examples |

|
| Additional Examples: |

|
Introduction
Today, we’re diving into the fascinating world of geometry with Heron's Formula. Have you ever wanted to calculate the area of a triangle without knowing its height?
For instance, consider a triangular park with sides measuring 40 m, 32 m, and 24 m. If we were to use the conventional formula for area, ½ x base x height.
We would need to know the height, which we don’t have. This is where Heron's Formula comes in, allowing us to find the area of a triangle using just the lengths of its three sides.
In this lesson, we will explore how to use Heron’s Formula step-by-step and apply it through engaging examples. So, get ready to unlock the secrets of triangles and discover the beauty of geometry!
Area of a Triangle — by Heron’s Formula
Heron, a mathematician born around 10 AD, made significant contributions to applied mathematics. His works covered various mathematical and physical subjects.
In his geometrical works, Heron derived the famous formula for the area of a triangle based on its three sides. This formula is now known as Heron's formula or Hero's formula
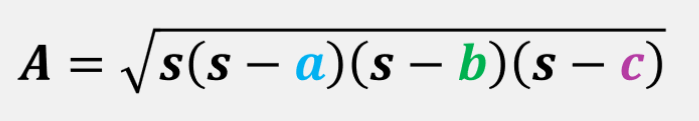
Here, a, b, and c are the sides of the triangle, and s is the semi-perimeter i.e sum of all-side divided by 2
s= (a+b+c) /2
Application of Heron's Formula
Let's apply Heron's formula to find the area of a triangular park with sides 40 cm, 32 cm, and 24 cm: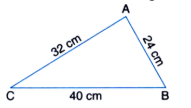
Let us take a = 40 cm, b = 24 cm, c = 32 cm,
Semi perimeter of the triangle (s) = (a + b + c)/2
s = (40 + 32 + 24)/2 = 48 cm
s −a = 48 − 40 = 8 cm
s −b = 48 − 24 = 24 cm
s −c = 48 − 32 = 16 cm
Area of the triangle = √[s(s-a)(s-b)(s-c)]

This matches the area calculated using the traditional method:
To ascertain the park's area, the application of the formula ½ × 32 × 24 square meters yields 384 cm².
Verification and Examples
Now, let's verify Heron's formula by applying it to other triangles:
Equilateral triangle (side =10 cm )

s= (a+b+c) /2
=> (10+10+10) /2
=> 30/2 =15
=> s= 15
replacing all values in the above area formulae we get ,
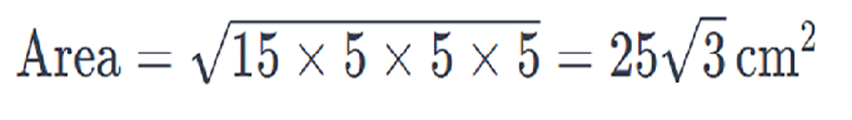
Additional Examples:
Example 1:
Given sides of triangle 8 cm, and 11 cm, and a perimeter of 32 cm, the area is calculated using Heron's formula:
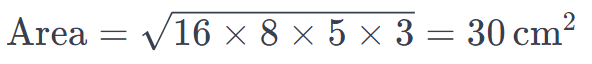
Example 2:
How much paper of each shade is needed to make a kite given in the figure, in which ABCD is a square with diagonal 44 cm.
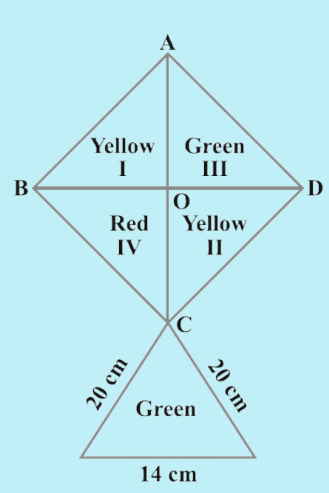
Solution:
According to the figure,
AC = BD = 44cm, AO = 44/2 = 22cm, BO = 44/2 = 22cm
From ΔAOB,
AB2 = AO2 + BO2
⇒ AB2 = 222 + 222
⇒ AB2 = 2 × 222
⇒ AB = 22√2 cm
Area of square ABCD = (Side)2
= (22√2)2
= 968 cm2
Area of each triangle (I, II, III, IV) = Area of square /4
= 968 /4
= 242 cm2
To find area of lower triangle,
Let a = 20, b = 20, c = 14
s = (a + b + c)/2
⇒ s = (20 + 20 + 14)/2 = 54/2 = 27.
Area of the triangle = √[s(s-a)(s-b)(s-c)]
= √[27(27-20)(27-20)(27-14)]
= √[27×7×7×13]
= 131.14 cm2
Therefore, We get,
Area of Red = Area of IV
= 242 cm2
Area of Yellow = Area of I + Area of II
= 242 + 242
= 484 cm2
Area of Green = Area of III + Area of the lower triangle
= 242 + 131.14
= 373.14 cm2
Example 3:
A triangular plot has sides in the ratio 3:5:7, and its perimeter is 300 m. The area is:
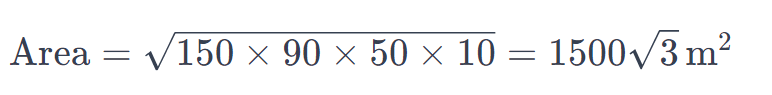
These examples illustrate Heron's formula as a powerful tool for finding triangle areas without relying on height.
|
40 videos|566 docs|57 tests
|
FAQs on Heron’s Formula Class 9 Notes Maths Chapter 10
| 1. What is Heron's Formula for calculating the area of a triangle? |  |
| 2. How do you calculate the semi-perimeter 's' of a triangle using Heron's Formula? |  |
| 3. Can Heron's Formula be used for any type of triangle? |  |
| 4. What are some examples of using Heron's Formula to find the area of a triangle? |  |
| 5. Why is Heron's Formula useful in geometry? |  |























