NCERT Exemplar Solutions: Coordinate Geometry | Mathematics (Maths) Class 9 PDF Download
Exercise 3.1
Q.1. Point (–3, 5) lies in the
(a) first quadrant
(b) second quadrant
(c) third quadrant
(d) fourth quadrant
Correct Answer is Option (b)
(-3,5) is of form (-x,y). In the point (-3, 5) abscissa is negative and ordinate is positive. So, it lies in the second quadrant. Hence, (B) is the correct option.
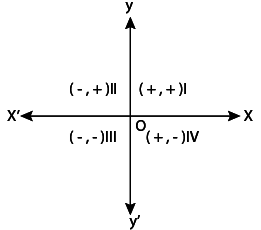
Q.2. Signs of the abscissa and ordinate of a point in the second quadrant are respectively
(a) +, +
(b) –, –
(c) –, +
(d) +, –
Correct Answer is Option (c)
We know that the x-coordinate is called the abscissa and y-coordinate is also called ordinate.
Thus in second quadrant abscissa is negative and ordinate is positive.
So that, the in the second quadrant, signs of the abscissa and ordinate is (–, +)
Therefore option (C) is correct
Q.3. Point (0, –7) lies
(a) on the x –axis
(b) in the second quadrant
(c) on the y-axis
(d) in the fourth quadrant
Correct Answer is Option (c)
Since the abscissa is 0, Point (0, –7) lies on the y-axis.
Hence, (C) is the correct option.
Q.4. Point (– 10, 0) lies
(a) on the negative direction of the x-axis
(b) on the negative direction of the y-axis
(c) in the third quadrant
(d) in the fourth quadrant
Correct Answer is Option (a)
Point (– 10, 0) lies on the negative direction of x-axis.
Hence, (a) is the correct option.
Q.5. Abscissa of all the points on the x-axis is
(a) 0
(b) 1
(c) 2
(d) any number
Correct Answer is Option (d)
Abscissa of all the points on the x-axis can be any number.
Hence, (D) is the correct option.
Q.6. Ordinate of all points on the x-axis is
(a) 0
(b) 1
(c) – 1
(d) any number
Correct Answer is Option (a)
Ordinate of all the points on the x-axis is 0.
Q.7. The point at which the two coordinate axes meet is called the
(a) abscissa
(b) ordinate
(c) origin
(d) quadrant
Correct Answer is Option (c)
The points at which the two coordinate axes meet is called the origin.
Hence, (C) is the correct option.
Q.8. A point both of whose coordinates are negative will lie in
(a) I quadrant
(b) II quadrant
(c) III quadrant
(d) IV quadrant
Correct Answer is Option (c)
A point both of whose coordinates are negative will lie in 3rd quadrant because; in 3rd quadrant, x-coordinate and y-coordinate are negative.
Q.9. Points (1, – 1), (2, – 2), (4, – 5), (- 3, – 4)
(a) lie in II quadrant
(b) lie in III quadrant
(c) lie in IV quadrant
(d) do not lie in the same quadrant
Correct Answer is Option (d)
In points (1, -1), (2, – 2) and (4, – 5), x-coordinate is positive and y-coordinate is negative. Therefore, they all lie in IV quadrant.
But in point (- 3, – 4), x-coordinate is negative and y-coordinate is negative. So, it lies in III quadrant. Hence, given points do not lie in the same quadrant.
Q10. If y coordinate of a point is zero, then this point always lies
(a) in I quadrant
(b) in II quadrant
(c) on x - axis
(d) on y - axis
Correct Answer is Option (c)
The coordinates of a point on the x-axis are of the form (x, 0) and that of the point on the y-axis is of the form (0, y).
Thus, if the y-coordinate of a point is zero, then this point always lies on the x-axis.
Hence, the correct answer is option (c).
Q.11. The points (- 5,2) and (2, – 5) lie in the
(a) same quadrant
(b) II and III quadrants, respectively
(c) II and IV quadrants, respectively
(d) IV and II quadrants, respectively
Correct Answer is Option (c)
In point (-5, 2), x-coordinate is negative and y-coordinate is positive, therefore it lies in II quadrant. In point (2, -5), x-coordinate is positive and y-coordinate is negative, therefore it lies in IV quadrant.
Q.12. If the perpendicular distance of a point P from the x-axis is 5 units and the foot of the perpendicular lies on the negative direction of x-axis, then the point P has
(a) x coordinate = – 5
(b) y coordinate = 5 only
(c) y coordinate = – 5 only
(d) y coordinate = 5 or –5
Correct Answer is Option (d)
We know that, the perpendicular distance of a point from the X-axis gives y-coordinate of that point. Here, foot of perpendicular lies on the negative direction of X-axis, so perpendicular distance can be measure in II quadrant or III quadrant. Hence, the point P has y-coordinate = 5 or -5.
Hence option D is correct.
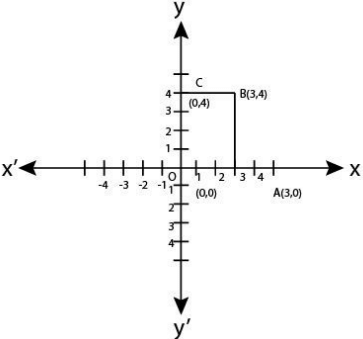
Q.13. On plotting the points O (0, 0), A (3, 0), B (3, 4), C (0, 4) and joining OA,
AB, BC and CO which of the following figure is obtained?
(a) Square
(b) Rectangle
(c) Trapezium
(d) Rhombus
Correct Answer is Option (b)
Here the point O(0,0) is the origin, A(3,0) lies on positive direction of x-axis. The point B(3,4) lies in 1st quadrant and C(0,4) lies on the positive direction of y-axis. On joining OA, AB, BC and CO the figure obtained is a rectangle.
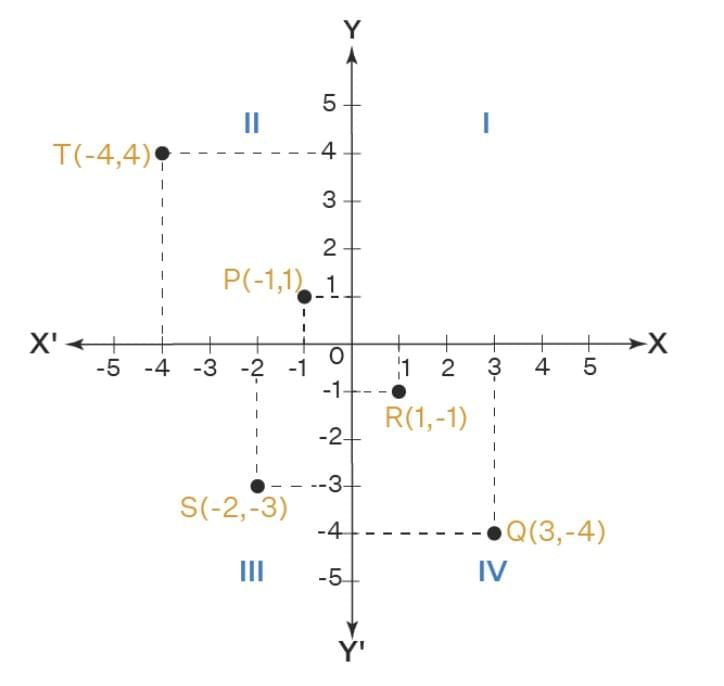
Q.14. If P (– 1, 1), Q (3, – 4), R(1, –1), S(–2, –3) and T (– 4, 4) are plotted on the graph paper, then the point(s) in the fourth quadrant are
(a) P and T
(b) Q and R
(c) Only S
(d) P and R
Correct Answer is Option (b)
We know that quadrant IV consists of all the points (x,y) for which x is positive and y negative, So, the points in the fourth quadrants are Q(3,−4) and R(1,−1).
Hence, (B) is the correct answer.
Q.15. If the coordinates of the two points are P (–2, 3) and Q(–3, 5), then (abscissa of P) – (abscissa of Q) is
(a) – 5
(b) 1
(c) – 1
(d) – 2
Correct Answer is Option (b)
Abscissa of P(−2, 3) = −2
Abscissa of Q(−3, 5) = −3
(Abscissa of P)−(Abscissa of Q) = −2−(−3) = −2+3 = 1
Hence, (B) is the correct answer.
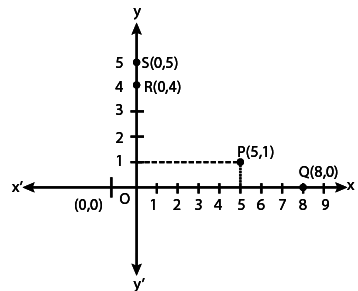
Q.16. If P (5, 1), Q (8, 0), R (0, 4), S (0, 5) and O (0, 0) are plotted on the graph paper, then the point(s) on the x-axis are
(a) P and R
(b) R and S
(c) Only Q
(d) Q and O
Correct Answer is Option (d)
We know that a point lies on x-axis If its y-coordinate is zero.
So, on plotting the given points on graph paper, we get Q and O lie on the x-axis.
Q.17. Abscissa of a point is positive in
(a) I and II quadrants
(b) I and IV quadrants
(c) I quadrant only
(d) II quadrant only
Correct Answer is Option (b)
The abscissa of a point is positive in I and IV quadrants.
Q.18. The points whose abscissa and ordinate have different signs will lie in
(a) I and II quadrants
(b) II and III quadrants
(c) I and III quadrants
(d) II and IV quadrants
Correct Answer is Option (d)
The points whose abscissa and ordinate have different signs will be of the form ( -x,y) or
(x, -y) and these points will lie in II and IV quadrants.
Q.19. In Fig. 3.1, coordinates of P are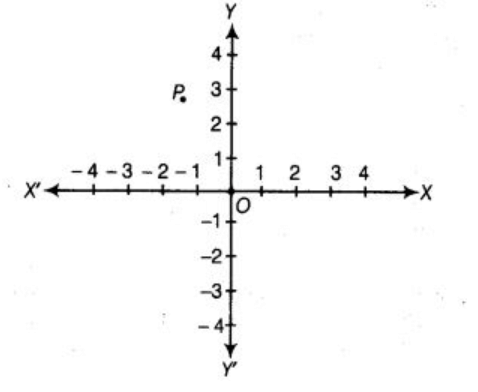 (a) (– 4, 2)
(a) (– 4, 2)
(b) (–2, 4)
(c) (4, – 2)
(d) (-1, 3)
Correct Answer is Option (d)
It is clear from the figure that, given point P lies in II quadrant, so its abscissa will be negative and ordinate will be positive. Also, its perpendicular distance from x-axis is 3, so y-coordinate of P is 3 and its perpendicular distance from y-axis is 1, so x-coordinate is -1. Therefore, coordinates of P are (-1, 3).
Q.20. In Fig. 3.2, the point identified by the coordinates (–5, 3) is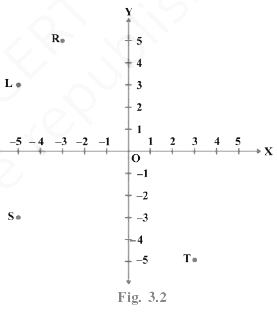 (a) T
(a) T
(b) R
(c) L
(d) S
Correct Answer is Option (c)
In point (-5, 3), x-coordinate is negative and y-coordinate is positive, so it will lie in II quadrant. Now, we see that perpendicular distance of L from V-axis is 5 and from X-axis is 3. So, the required point is L.
Q.21. The point whose ordinate is 4 and which lies on y-axis is
(a) (4, 0)
(b) (0, 4)
(c) (1, 4)
(d) (4, 2)
Correct Answer is Option (b)
The point on the y-axis has its abscissa 0.
So, the point whose ordinate is 4 and which lies on the y-axis is (0,4).
Q.22. Which of the points P(0, 3), Q(1, 0), R(0, – 1), S(–5, 0), T(1, 2) do not lie on the x-axis?
(a) P and R only
(b) Q and S only
(c) P, R and T
(d) Q, S and T
Correct Answer is Option (c)
We know that, if a point is of the form, (x,0) i.e its y-coordinate is zero, then it will lie on x-axis otherwise not.
Here, y-coordinates of points P(0, 3), R(0, -1) and T(1, 2) is not zero, so these points do not lie on the x-axis.
Q.23. The point which lies on y-axis at a distance of 5 units in the negative direction of y-axis is
(a) (0, 5)
(b) (5, 0)
(c) (0, – 5)
(d) (– 5, 0)
Correct Answer is Option (c)
Given that the point lies on y-axis, shows that its x-coordinate is zero. The point is at a distance of 5 units in the negative direction of y-axis so its y-coordinate is negative. Hence, the required point is (0,-5).
Q.24. The perpendicular distance of the point P (3, 4) from the y-axis is
(a) 3
(b) 4
(c) 5
(d) 7
Correct Answer is Option (a)
The perpendicular distance of the point from Y-axis measured along X-axis is abscissa of the point. So, the answer is 3 units.
Exercise 3.2
Q.1. Write whether the following statements are True or False? Justify your answer.
(i) Point (3, 0) lies in the first quadrant.
False, because if ordinate of a point is zero, the point lies on the x-axis.
(ii) Points (1, –1) and (–1, 1) lie in the same quadrant.
False (1, –1 ), lies in IV quadrant and (–1, 1) lies in II quadrant.
(iii) The coordinates of a point whose ordinate is 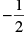 and abscissa is 1 are
and abscissa is 1 are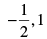 .
.
False, because in the coordinates of a point abscissa comes first and then the ordinate.
(iv) A point lies on y-axis at a distance of 2 units from the x-axis. Its coordinates are (2, 0).
False, because a point on the y-axis is of the form (0, y).
(v) (–1, 7) is a point in the II quadrant.
True, because in the II quadrant, signs of abscissa and ordinate are –, +, respectively.
Exercise 3.3
Q.1. Write the coordinates of each of the points P, Q, R, S, T and O from the Fig. 3.5.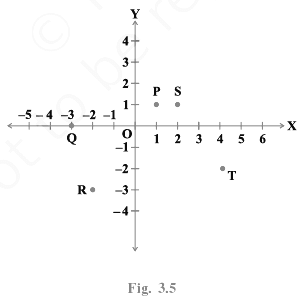
Given, the figure represents the points O, P, Q, R, S and T plotted on the graph.
From the figure, we observe that
The points P and S lie in the first quadrant.
In first quadrant the abscissa and ordinate are positive
The perpendicular distance from x-axis is 1 unit and y-axis is 1 unit.
Coordinates of P = (1, 1)
The perpendicular distance from x-axis is 1 unit and y-axis is 2 units.
Coordinates of S = (2, 1)
The point Q lies on the negative x-axis.
So the ordinate is 0
Coordinates of Q = (-3, 0)
The point R lies in the third quadrant.
In third quadrant the abscissa and ordinate are negative
The perpendicular distance from x-axis is 2 units and y-axis is 3 units.
Coordinates of R = (-3, -2)
The point T lies in the fourth quadrant.
In the fourth quadrant, abscissa is positive and ordinate is negative.
The perpendicular distance from x-axis is 2 units and y-axis is 4 units.
Coordinates of T = (4, -2)
The point O is the intersection of both the axes.
The point O is the origin.
Coordinates of O are (0, 0).
Q.2. Plot the following points and write the name of the figure obtained by joining them in order:
P(– 3, 2), Q (– 7, – 3), R (6, – 3), S (2, 2)
Plot P(– 3, 2), Q (– 7, – 3), R (6, – 3), S (2, 2) on the graph and join PQ, QR, RS and SP.
We can see that PQRS is in the shape of trapezium.
Hence, the figure obtained is a trapezium.
Q.3. Plot the points (x, y) given by the following table:
On plotting the given points on the graph, we get the points P(2, 4), Q(4, 2) R(–3, 0), S(–2, 5), T(3, – 3) and O(0, 0)
Q.4. Plot the following points and check whether they are collinear or not:
(i) (1, 3), (– 1, – 1), (– 2, – 3)
(ii) (1, 1), (2, – 3), (– 1, – 2)
(iii) (0, 0), (2, 2), (5, 5)
The points that are collinear are those that are on the same straight line or on a single line. In Euclidean geometry, two or more points on a line that are close to or far from each other are said to be collinear.
(i)The points (1, 3), (– 1, – 1), (– 2, – 3) lie in a straight line,
Hence, the points are collinear.
(ii)The points (1, 1), (2, – 3), (– 1, – 2) do not lie in a straight line,
Hence, the points are not collinear.
(iii)The points (0, 0), (2, 2), (5, 5) lie in a straight line,
Hence, the points are collinear.
Q.5. Without plotting the points indicate the quadrant in which they will lie, if
(i) ordinate is 5 and abscissa is – 3
(ii) abscissa is – 5 and ordinate is – 3
(iii) abscissa is – 5 and ordinate is 3
(iv) ordinate is 5 and abscissa is 3
(i) The point is (-3,5).
Hence, the point lies in the II quadrant.
(ii) The point is (-5,-3).
Hence, the point lies in the III quadrant.
(iii) The point is (-5,3).
Hence, the point lies in the II quadrant.
(iv) The point is (3,5).
Hence, the point lies in the I quadrant.
Q.6. In Fig. 3.6, LM is a line parallel to the y-axis at a distance of 3 units.
(i) What are the coordinates of the points P, R and Q?
(ii) What is the difference between the abscissa of the points L and M?
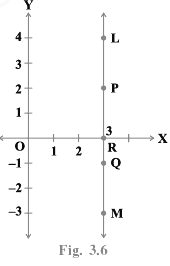
Given LM is a line parallel to the Y - axis and its perpendicular distance from Y - axis is 3 units
(i) Coordinates of point P = (3, 2)
[Since,itsperpendiculardistancefrom X − axis is 2]
Coordinate of point Q = (3, − 1)
[Since, its perpendicular distance from X − axis is 1 in negative direction of Y−axis].
Coordinate of point R = (3, 0) [since its lies on X - axis, so its y-coordinate is zero.]
(ii) Abscissa of point L = 3, abscissa of point M = 3
∴ Difference between the abscissa of the points L and M = 3 − 3 = 0
Q.7. In which quadrant or on which axis each of the following points lie? (– 3, 5), (4, – 1), (2, 0), (2, 2), (– 3, – 6)
(i) In point (−3,5), x - coordinate is negative and y - coordinate is positive, so it lies in II quadrant.
(ii) In point (4,−1), x - coordinate is positive and y - coordinate is negative, so it lies in IV quadrant.
(iii) In point (2,0), x - coordinate is positive and y - coordinate is zero, so it lies on X - axis.
(iv) In point (2,2), x-coordinate and y - coordinate both are positive, so its lies in I quadrant.
(v) In point (−3,−6), x - coordinate and y - coordinate both are negative, so its lies in III quadrant.
Q.8. Which of the following points lie on y-axis?
A (1, 1), B (1, 0), C (0, 1), D (0, 0), E (0, – 1), F (– 1, 0), G (0, 5), H (– 7, 0), I (3, 3).
Given, the points are A (1, 1), B (1, 0), C (0, 1), D (0, 0), E (0, - 1), F (- 1, 0), G (0, 5), H (- 7, 0), I (3, 3).
We have to find the points which lie on the y-axis.
Considering the point A(1, 1)
The x-coordinate is 1 and the y-coordinate is 1
The point A lies on the first quadrant
Considering the point B(1, 0)
The x-coordinate is 1 and y-coordinate is 0.
The point B lies on the x-axis
Considering the point C(0, 1)
The x-coordinate is 0 and the y-coordinate is 1
The point C lies on the y-axis
Considering the point D(0, 0)
The x-coordinate is 0 and y-coordinate is 0.
The point D is the point of intersection of both axes
The point D is the origin.
Considering the point E(0, -1)
The x-coordinate is 0 and the y-coordinate is -1
The point E lies on the negative y-axis.
Considering the point F(-1, 0)
The x-coordinate is -1 and the y-coordinate is 0
The point F lies on the negative x-axis
Considering the point G(0, 5)
The x-coordinate is 0 and the y-coordinate is 5
The point G lies on the y-axis
Considering the point H(-7, 0)
The x-coordinate is -7 and the y-coordinate is 0
The point H lies on the negative x-axis
Considering the point I(3, 3)
The x-coordinate is 3 and the y-coordinate is 3
The point I lies on the first quadrant.
Therefore, the points C, D, E and G lie on the y-axis.
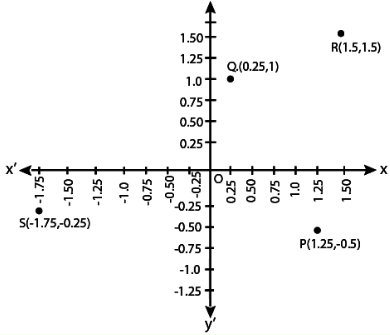
Q.9. Plot the points (x, y) given by the following table.
Use scale 1 cm = 0.25 units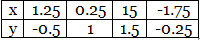
Let X’ OX and Y’ OY be the coordinate axes.
Plot the given points (1.25, -0.5), (0.25, 1), (1.5, 1.5) and (-1.75, - 0.25) on the graph paper.
After plotting, we get the points P (1.25, -0.5), Q (0.25, 1), R (1.5, 1.5) and S(-1.75, - 0.25).
Q.10. A point lies on the x-axis at a distance of 7 units from the y-axis. What are its coordinates? What will be the coordinates if it lies on y-axis at a distance of –7 units from x-axis?
Given point lies on the positive direction of x−axis, so its y- coordinate will be zero and it is at a distance of 7 units from the y - axis, so its coordinate are (7,0).
If it lies on negative direction of y - axis, then its x- coordinate will be zero and its distance from x - axis is 7 units, so its coordinate are (0,−7)
Q.11. Find the coordinates of the point
(i) which lies on x and y axes both.
(ii) whose ordinate is – 4 and which lies on y-axis.
(iii) whose abscissa is 5 and which lies on x-axis.
(i) The point which lies on x and y-axes both is origin whose coordinates are (0, 0).
(ii) The point whose ordinate is - 4 and which lies on the y-axis, i.e., whose x-coordinate is zero is (0, -4).
(iii) The point whose abscissa is 5 and which lies on the x-axis, i.e., whose y-coordinate is zero is (5, 0).
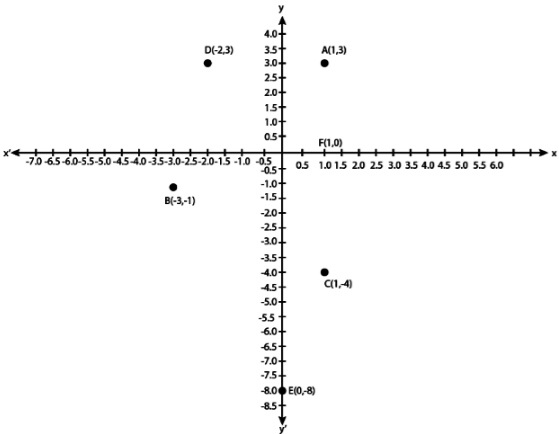
Q.12. Taking 0.5 cm as 1 unit, plot the following points on the graph paper :
A (1, 3), B (– 3, – 1), C (1, – 4), D (– 2, 3), E (0, – 8), F (1, 0)
Here, in point A(1, 3) both x and y-coordinates are positive, so it lies in I quadrant.
In point B(-3, -1) both x, and y-coordinates are negative, so it lies in III quadrant.
In point C(1, -4), x-coordinates is positive and y-coordinate is negative. So it lies in IV quadrant.
In point D(-2, 3), x-coordinate is negative and y-coordinate is positive, so it lies in II quadrant.
In point E(0, -8) x-coordinate is zero, so it lies on the y-axis and in Point F(1,0) y-coordinate is zero, so it lies on the x-axis.
On plotting the given points, we get the following graph
Exercise 3.4
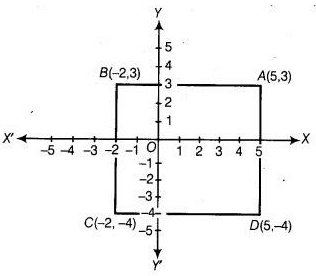
Q.1. Points A (5, 3), B (– 2, 3) and D (5, – 4) are three vertices of a square ABCD. Plot these points on a graph paper and hence find the coordinates of the vertex C.
Take a point C on the graph such that ABCD is a square i.e., all sides AB,BC,CDandAD are equal.
So, abscissa of C should be equal to abscissa of B that is, −2 and ordinate of C should be equal to ordinate of D that is, −4. Hence, the coordinates of C are (−2,–4).
The graph obtained by plotting the points A,B,C,D is given below.
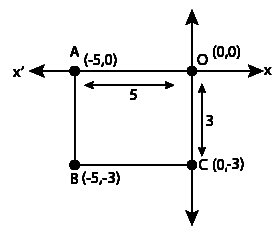
Q.2. Write the coordinates of the vertices of a rectangle whose length and breadth are 5 and 3 units respectively, one vertex at the origin, the longer side lies on the x-axis and one of the vertices lies in the third quadrant.
Given, length of a rectangle = 5 units
Breadth of a rectangle = 3 units
One vertex is at origin i.e, (0, 0) and one of the other vertices lies in III quadrant.
So, the length of the rectangle is 5 units in the negative direction of x-axis and then the vertex A is (-5, 0).
Also, the breadth of the rectangle is 3 units in the negative direction of the y-axis and then the vertex C is (0,-3). The fourth vertex B is (-5,-3).
Q.3. Plot the points P (1, 0), Q (4, 0) and S (1, 3). Find the coordinates of the point R such that PQRS is a square.
Given, PQRS is a square
The coordinates of P, Q and S are (1, 0), (4, 0) and (1, 3)
We have to find the coordinates of the point R.
Considering the point P(1, 0)
The x-coordinate is positive and the y-coordinate is 0
Therefore, the point P lies on the x-axis
Considering the point Q(4, 0)
The x-coordinate is positive and the y-coordinate is 0
Therefore, the point Q lies on the x-axis
Considering the point S(1, 3)
The x-coordinate is positive and the y-coordinate is positive
Therefore, the point S lies in the first quadrant
Now plotting the points P, Q and S,
We know that all the sides of a square are equal.
In the given square PQRS, the sides PQ = QR = RS = PS
The abscissa of the point Q is equal to the abscissa of the point R
So, the abscissa of the point R = 4
The ordinate of the point S is equal to the ordinate of the point R
So, the ordinate of the point R = 3
Therefore, the coordinates of R = (4, 3)
Q.4. From the Fig. 3.8, answer the following:
(i) Write the points whose abscissa is 0.
(ii) Write the points whose ordinate is 0.
(iii) Write the points whose abscissa is – 5.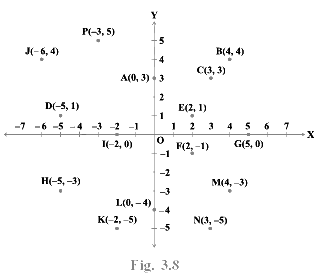
(i) Clearly, the distance of points A, L and O from y - axis is 0. So, A(0, 3), L(0, −4) and O(0, 0) are the points whose abscissa is 0.
(ii) Clearly, the distance of points G, I and O from x - axis is 0. So, (5, 0), I(−2, 0) and O(0, 0) are the points whose ordinate is 0.
(iii) Clearly, the distance of points H and D from y - axis is 5 units and both lien in second and third quadrants respectively. So, (−5, −3) and D(−5, 1) are the points whose abscissa is −5.
Q.5. Plot the points A (1, – 1) and B (4, 5)
(i) Draw a line segment joining these points.
Write the coordinates of a point on this line segment between the points A and B.
(ii) Extend this line segment and write the coordinates of a point on this line that lies outside the line segment AB.
In point A(1, -1) x-coordinate is positive and y-coordinate is negative, so it lies in IV quadrant.
In Point B(4, 5), both coordinates are positive, so it lies in I quadrant. On Plotting these point we get the following graph.(i) On joining the points A and B, we get the line segment AB. Now to find the coordinates of a point on this line segment between A and B draw a perpendicular to X-axis from x = 2. [Since, x = 2 lies between A and B] say it intersects line segment AB at P. Now, draw a perpendicular to Y-axis from P, it intersects Y– axis at y = 1. Thus we get points (2, 1) which lie between line segment AB.
(ii) Extend the line segment AB. Now draw a perpendicular to X-axis from x = 0, say it intersects extended line segment at Q on Y– axis at y = – 3. Thus, we get the point Q(0, – 3) which lies outside the line segment AB.
|
40 videos|471 docs|57 tests
|
FAQs on NCERT Exemplar Solutions: Coordinate Geometry - Mathematics (Maths) Class 9
| 1. What is the importance of NCERT Exemplar Solutions in understanding Coordinate Geometry? |  |
| 2. How can I use NCERT Exemplar Solutions to improve my performance in Coordinate Geometry? |  |
| 3. Are NCERT Exemplar Solutions sufficient for mastering Coordinate Geometry for exams? |  |
| 4. What types of questions can I expect from Coordinate Geometry in NCERT exams? |  |
| 5. How can I effectively practice Coordinate Geometry using NCERT Exemplar Solutions? |  |