Fundamental Theorems of Vector Calculus | Engineering Mathematics - Engineering Mathematics PDF Download
Theorems in Vector Calculus
The four fundamental theorems of vector calculus are generalizations of the fundamental theorem of calculus. The fundamnetal theorem of calculus equates the integral of the derivative G′(t) to the values of G(t) at the interval boundary points: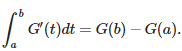
Similarly, the fundamental theorems of vector calculus state that an integral of some type of derivative over some object is equal to the values of function along the boundary of that object.
- We can speak of all the fundamental theorems using the same language. (If the additional abstraction used to show these theorems are similar is not helpful, you can skip this paragraph.) We have fundamental theorems for one-dimensional (curves), two-dimensional (planar regions and surfaces), and three-dimensional (volumes) objects. If an object is n-dimensional, then its boundary is (n−1)-dimensional, by definition.
- Therefore, we can say that a fundamental theorem takes an n-dimensional integral of some derivative to an (n−1)-dimensional integral over the boundary of the original object. (If we start with a one-dimensional object, then we'll understand the “zero-dimensional integral” over the boundary as just the evaluation of the integral at its endpoints.)
- If you wanted to understand why these theorems are all so similar, you could do some research into how all four theorems are special cases of something called the generalized Stokes' theorem.
- Recognizing the similarity of the four fundamental theorems can help you understand and remember them. Here we summarize the theorems and outline their relationships to the various integrals you learned in multivariable calculus.
The fundamental theorems are:
- the gradient theorem for line integrals,
- Green's theorem,
- Stokes' theorem, and
- the divergence theorem.
The Gradient Theorem for Line Integrals
The gradient theorem for line integrals relates a line integral to the values of a function at the “boundary” of the curve, i.e., its endpoints. It says that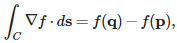 where p and q are the endpoints of C. In words, this means the line integral of the gradient of some function is just the difference of the function evaluated at the endpoints of the curve. In particular, this means that the integral of ∇f does not depend on the curve itself. The vector field ∇f is conservative (also called path-independent).
where p and q are the endpoints of C. In words, this means the line integral of the gradient of some function is just the difference of the function evaluated at the endpoints of the curve. In particular, this means that the integral of ∇f does not depend on the curve itself. The vector field ∇f is conservative (also called path-independent).
Often, we are not given the potential function, but just the integral in terms of a vector field F: ∫cF⋅ds. We can use the gradient theorem only when F is conservative, in which case we can find a potential function f so that ∇f = F. Then,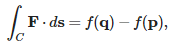
where p and q are the endpoints of C.
Even if you can't find f, but still know that F is conservative, you could use the gradient theorem for line integrals to change the line integral of F over C to the line integral of F over any other curve with the same endpoints. Moreover, the integral of any conservative F over a closed curve is zero.
Green's Theorem
Green's theorem relates a double integral over a region to a line integral over the boundary of the region. If a curve C is the boundary of some region D, i.e., C = ∂D, then Green's theorem says that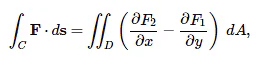
as long as F is continously differentiable everywhere inside D. The integrand of the double integral can be thought of as the “microscopic circulation” of F. Green's theorem then says that the total “microscopic circulation” in D is equal to the circulation ∫cF⋅ds around the boundary C = ∂D. Thinking of Green's theorem in terms of circulation will help prevent you from erroneously attempting to use it when C is an open curve.
In order for Green's theorem to work, the curve C has to be oriented properly. Outer boundaries must be counterclockwise and inner boundaries must be clockwise.
Stokes' Theorem
Stokes' theorem relates a line integral over a closed curve to a surface integral. If a path C is the boundary of some surface S, i.e., C = ∂S, then Stokes' theorem says that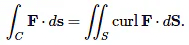 The integrand of the surface integral can be thought of as the “microscopic circulation” of F. Stokes' theorem then says that the total “microscopic circulation” in S is equal to the circulation ∫cF⋅ds around the boundary C = ∂S. Thinking of Stokes' theorem in terms of circulation will help prevent you from erroneously attempting to use it when C is an open curve.
The integrand of the surface integral can be thought of as the “microscopic circulation” of F. Stokes' theorem then says that the total “microscopic circulation” in S is equal to the circulation ∫cF⋅ds around the boundary C = ∂S. Thinking of Stokes' theorem in terms of circulation will help prevent you from erroneously attempting to use it when C is an open curve.
- In order for Stokes' theorem to work, the curve C has to be a positively oriented boundary of the surface S. To check for proper orientation, use the right hand rule.
- Since the line integral ∫cF⋅ds depends only on the boundary of S (remember C=∂S), the surface integral on the right hand side of Stokes' theorem must also depend only on the boundary of S.
- Therefore, Stokes' theorem says you can change the surface to another surface S′, as long as ∂S′=∂S. This works, of course, only when integrating the vector field curlF over a surface; it won't work for any arbitrary vector field.
The Divergence Theorem
The divergence theorem relates a surface integral to a triple integral. If a surface S is the boundary of some solid W, i.e., S = ∂W, then the divergence theorem says that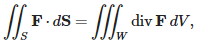 where we orient S so that it has an outward pointing normal vector.
where we orient S so that it has an outward pointing normal vector.
The integrand of the triple integral can be thought of as the expansion of some fluid. The divergence theorem then says that the total expansion of the fluid in W is equal to the total flux of the fluid out of the boundary S = ∂W.
|
65 videos|129 docs|94 tests
|
















