BCD to Excess-3 & Excess-3 to BCD Conversion | Digital Circuits - Electronics and Communication Engineering (ECE) PDF Download
Introduction
- To understand the process of converting BCD to Excess-3, it is required to have knowledge of Number System and Number Base Conversion.
- The Excess-3 binary code is an example of a self-complementary BCD code. A self-complementary binary code is a code which is always complimented in itself. By replacing the bit 0 to 1 and 1 to 0 of a number, we find the 1's complement of the number. The sum of the 1'st complement and the binary number of a decimal is equal to the binary number of decimal 9.
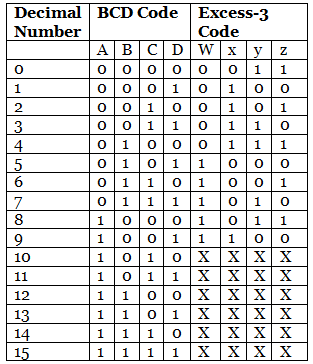
- The process of converting BCD to Excess-3 is quite simple from other conversions. The Excess-3 code can be calculated by adding 3, i.e., 0011 to each four-digit BCD code. Below is the truth table for the conversion of BCD to Excess-3 code. In the below table, the variables A, B, C, and D represent the bits of the binary numbers. The variable 'D' represents the LSB, and the variable 'A' represents the MSB. In the same way, the variables w, x, y, and z represent the bits of the Excess-3 code. The variable 'z' represents the LSB, and the variable 'w' represents the MSB. The 'don't care conditions' is expressed by the variable 'X'.
Now, we will use the K-map method to design the logical circuit for the conversion of BCD to Excess-3 code as: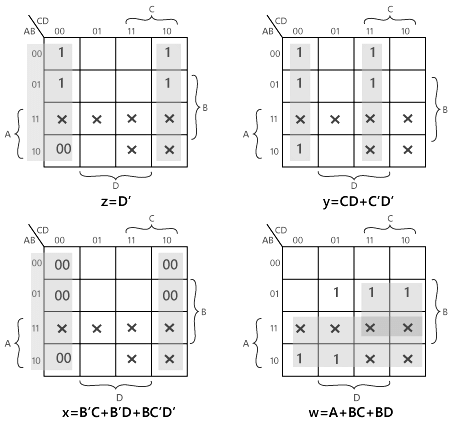 So,
So,
w = A + BC + BD
x = B' C + B' D + BC' D'
y = CD + C'D'
z = D'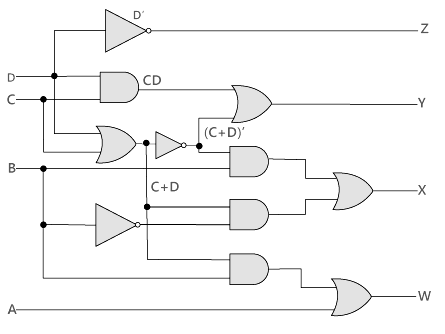
Example: (100001011001)BCD
To find the Excess-3 code of the given Excess-3 code, first, we will make the group of 4 bits from right to left. Then, we will add 0011 in each group of 4 bits in order to get the excess-3 code.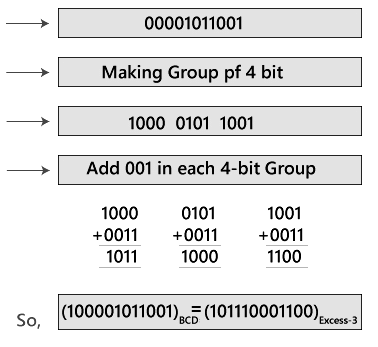
Excess-3 to BCD conversion
The process of converting Excess-3 to BCD is opposite to the process of converting BCD to Excess-3. The BCD code can be calculated by subtracting 3, i.e., 0011 from each four-digit Excess-3 code. Below is the truth table for the conversion of Excess-3 code to BCD. In the below table, the variables w, x, y, and z represent the bits of the Excess-3 code. The variable 'z' represents the LSB, and the variable 'w' represents the MSB. In the same way, the variables A, B, C, and D represent the bits of the binary numbers. The variable 'D' represents the LSB, and the variable 'A' represents the MSB. The 'don't care conditions' is defined by the variable 'X'.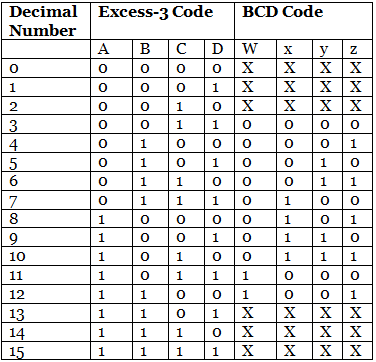 Now, we will use the K-map method to design the logical circuit for the conversion of Excess-3 code to BCD as:
Now, we will use the K-map method to design the logical circuit for the conversion of Excess-3 code to BCD as: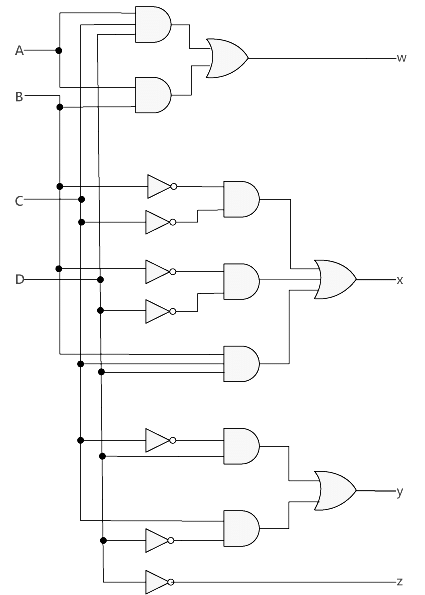 So,
So,
w=AB+ACD
B=x' y'+x' z'+xyz
C=y' z+yz'
D=z'
Example: (101110001100)Excess-3
To find the BCD code of the given BCD number, first, we make the group of 4 bits from right to left. Then, we subtract 0011 in each group of 4 bits in order to get the BCD code.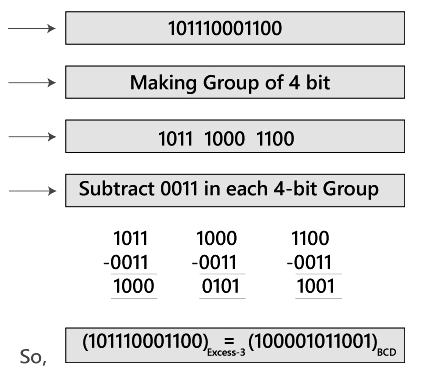
|
76 videos|175 docs|70 tests
|
















