Combinational Logic Circuits | Digital Circuits - Electronics and Communication Engineering (ECE) PDF Download

The combinational logic circuits are the circuits that contain different types of logic gates. Simply, a circuit in which different types of logic gates are combined is known as a combinational logic circuit. The output of the combinational circuit is determined from the present combination of inputs, regardless of the previous input. The input variables, logic gates, and output variables are the basic components of the combinational logic circuit. There are different types of combinational logic circuits, such as Adder, Subtractor, Decoder, Encoder, Multiplexer, and De-multiplexer.

There are the following characteristics of the combinational logic circuit:

• At any instant of time, the output of the combinational circuits depends only on the present input terminals.
• The combinational circuit doesn't have any backup or previous memory. The present state of the circuit is not affected by the previous state of the input.
• The n number of inputs and m number of outputs are possible in combinational logic circuits.

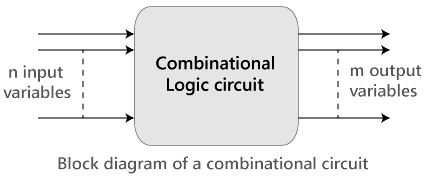The 'n' input variable comes from the external source while the 'm' output variable goes to the external destination. In many applications, the source or destinations are storage registers.

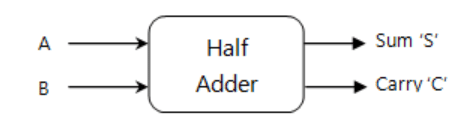
Half Adder

The half adder is a fundamental component in computer arithmetic, responsible for adding two individual binary digits. When we have two binary digits, A and B, the half adder combines them using a circuit that produces two outcomes: the sum and the carry. The carry accounts for any excess resulting from the addition of these two numbers. This concept is visually illustrated in the block diagram shown below.

Truth Table of Half Adder:

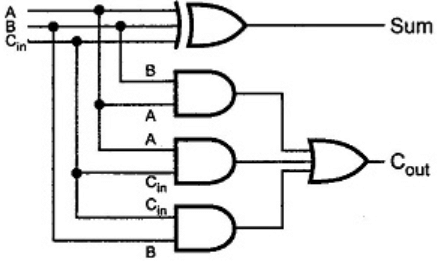
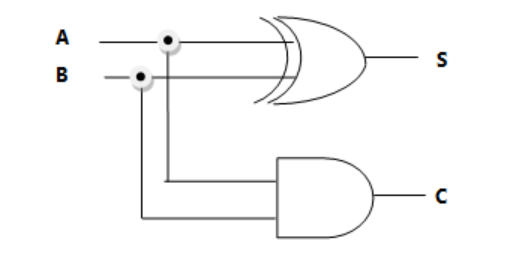Half Adder - Logic Circuit

The sum S is represented by the Boolean Expression S = A'B + AB' and C = AB

Full Adder

The half adder is used to add only two numbers. To overcome this problem, the full adder was developed. The full adder is used to add three 1-bit binary numbers A, B, and carry C. The full adder has three input states and two output states i.e., sum and carry.

Half adder + Cin = Full Adder

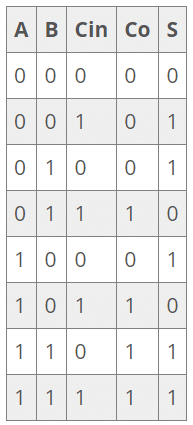
The next truth table shown here demonstrates all the possible outputs for various input combinations with the carry input digit:

Truth Table - Full Adder:

Boolean expression for the full adder is S = A'B'Cin + A'BCin' + AB'Cin' + ABCin and C = A'BCin + AB'Cin + ABCin' + ABCin. This is where A and B are all the possible binary inputs and C is the carry in. For example, if A is 0 and B is 0 and the Cin is 1, then:

S = (0'0'1)+(0'01')+(00'1')+(001) = (111)+(100)+(010)+(001) = (1)+(0)+(0)+(0) = 1

C = (0'01)+(00'1)+(001')+(001) = (101)+(011)+(000)+(001) = (0)+(0)+(0)+(0) = 0

S = 1 and C = 0

Full Adder - Logic Circuit

Subtractors

A subtractor serves the purpose of deducting one numerical value from another. In the context of binary arithmetic, subtraction is accomplished using the 1's complement and 2's complement representations of the numbers involved. This process requires the manipulation of three key binary bits: the minuend (X), the subtrahend (Y), and the borrow (Bi), which is derived from the preceding bit's result. The outcome of this operation is twofold: it yields the difference (D) and also provides the next borrow bit (Bout).

Half Subtractors

The half subtractor is also a building block of subtracting two binary numbers. It has two inputs and two outputs. This circuit is used to subtract two single bit binary numbers A and B. The 'diff' and 'borrow' are the two output state of the half adder.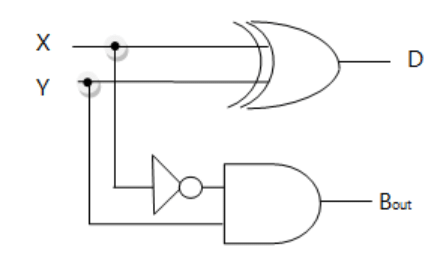

Half Subtractor - Logic Circuit

Truth Table - Half Subtractor

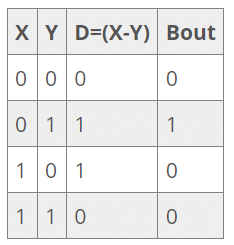
The Boolean expressions are as follows:

D = X'Y + XY'

Bout = X'Y

Example: If our inputs X and Y are 0 and 1, then compliment of 0 is 1 and vice versa.

D = (0'1)+(01') = (11)+(00) = 1 and Bout = (0'1) = (11) = 1

Full Subtractor

The Half Subtractor is used to subtract only two numbers. To overcome this problem, full subtractor was designed. The full subtractor is used to subtract three 1-bit numbers A, B, and C, which are minuend, subtrahend, and borrow, respectively. The full subtractor has three input states and two output states i.e., diff and borrow.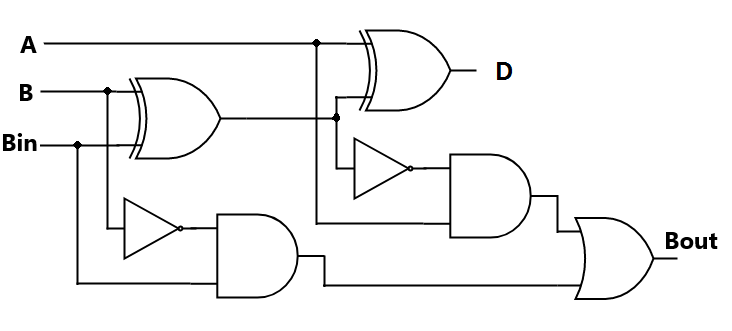

Full Subtractor - Logic Circuit

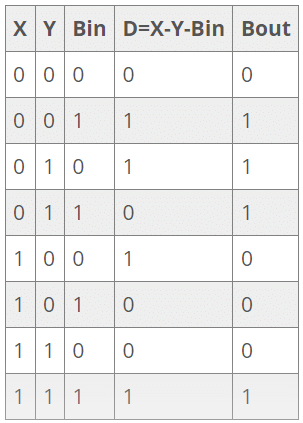
Truth Table - Full Subtractor:

Multiplexers

The multiplexer is a combinational circuit that has n-data inputs and a single output. It is also known as the data selector which selects one input from the inputs and routes it to the output. With the help of the selected inputs, one input line from the n-input lines is selected. The enable input is denoted by E, which is used in cascade.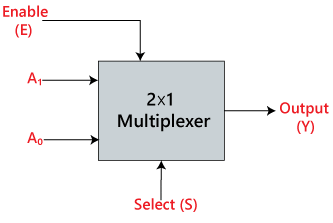

De-multiplexers

A De-multiplexer performs the reverse operation of a multiplexer. The de-multiplexer has only one input, which is distributed over several outputs. One output line is selected at a time by selecting lines. The input is transmitted to the selected output line.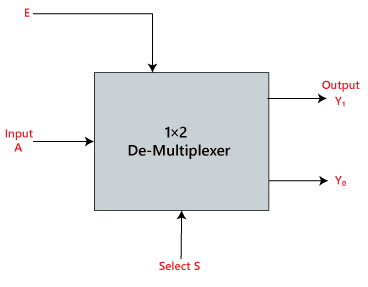

Decoder

A decoder is a combinational circuit having n inputs and to a maximum of m = 2n outputs. The decoder is the same as the de-multiplexer. The only difference between de-multiplexer and decoder is that in the decoder, there is no data input. The decoder performs an operation that is completely opposite of an encoder.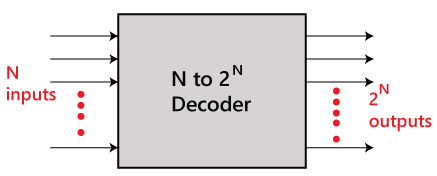

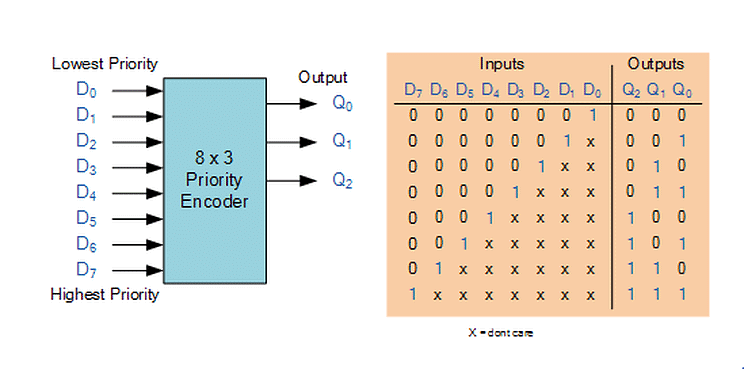
Encoder

The encoder is used to perform the reverse operation of the decoder. An encoder having n number of inputs and m number of outputs is used to produce m-bit binary code which is related to the digital input number. The encoder takes the digital word and converts it into another digital word.