What is Ratio? | Mathematics for Digital SAT PDF Download
Ratio
Ratio, in math, is a term that is used to compare two or more numbers. It is used to indicate how big or small a quantity is when compared to another. In a ratio, two quantities are compared using division. Here the dividend is called the 'antecedent' and the divisor is called the 'consequent'. For example, in a group of 30 people, 17 of them prefer to walk in the morning and 13 of them prefer to cycle. To represent this information as a ratio, we write it as 17: 13. Here, the symbol ': ' is read as "is to". So, the ratio of people who prefer walking to the people who prefer cycling is read as '17 is to 13'.
What is Ratio?
The ratio is defined as the comparison of two quantities of the same units that indicates how much of one quantity is present in the other quantity. Ratios can be classified into two types. One is part to part ratio and the other is part to whole ratio. The part-to-part ratio denotes how two distinct entities or groups are related. For example, the ratio of boys to girls in a class is 12: 15, whereas, the part-to-whole ratio denotes the relationship between a specific group to a whole. For example, out of every 10 people, 5 of them like to read books. Therefore, the part to the whole ratio is 5: 10, which means every 5 people from 10 people like to read books.
Ratio Formula
We use the ratio formula while comparing the relationship between two numbers or quantities. The general form of representing a ratio of between two quantities say 'a' and 'b' is a: b, which is read as 'a is to b'.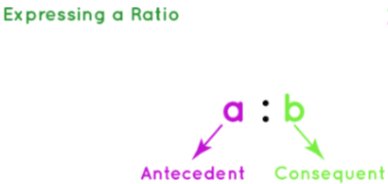
The fraction form that represents this ratio is a/b. To further simplify a ratio, we follow the same procedure that we use for simplifying a fraction. a:b = a/b. Let us understand this with an example.
Example: In a class of 50 students, 23 are girls and the remaining are boys. Find the ratio of the number of boys to the number of girls.
Total number of students = 50; Number of girls = 23.
Total number of boys = Total number of students - Total number of girls = 50 - 23 = 27
Therefore, the desired ratio is, (Number of boys: Number of girls), which is 27 : 23.
Calculation of Ratios
In order to calculate the ratio of two quantities, we can use the following steps. Let us understand this with an example. For example, if 15 cups of flour and 20 cups of sugar are needed to make fluffy pancakes, let us calculate the ratio of flour and sugar used in the recipe.
- Step 1: Find the quantities of both the scenarios for which we are determining the ratio. In this case, it is 15 and 20.
- Step 2: Write it in the fraction form a/b. So, we write it as 15/20.
- Step 3: Simplify the fraction further, if possible. The simplified fraction will give the final ratio. Here, 15/20 can be simplified to 3/4.
- Step 4: Therefore, the ratio of flour to sugar can be expressed as 3: 4.
How to Simplify Ratios?
A ratio expresses how much of one quantity is required as compared to another quantity. The two terms in the ratio can be simplified and expressed in their lowest form. Ratios when expressed in their lowest terms are easy to understand and can be simplified in the same way as we simplify fractions. To simplify a ratio, we use the following steps. Let us understand this with an example. For example, let us simplify the ratio 18:10.
- Step 1: Write the given ratio a:b in the form of a fraction a/b. On writing the ratio in the fraction form, we get 18/10.
- Step 2: Find the greatest common factor of 'a' and 'b'. In this case, the GCF of 10 and 18 is 2.
- Step 3: Divide the numerator and denominator of the fraction with the GCF to obtain the simplified fraction. Here, by dividing the numerator and denominator by 2, we get, (18÷2)/(10÷2) = 9/5.
- Step 4: Represent this fraction in the ratio form to get the result. Therefore, the simplified ratio is 9:5.
Tips and Tricks on Ratio:
- In case both the numbers 'a' and 'b' are equal in the ratio a: b, then a: b = 1.
- If a > b in the ratio a : b, then a : b > 1.
- If a < b in the ratio a : b, then a : b < 1.
- It is to be ensured that the units of the two quantities are similar before comparing them.
Equivalent Ratios
Equivalent ratios are similar to equivalent fractions. If the antecedent (the first term) and the consequent (the second term) of a given ratio are multiplied or divided by the same number other than zero, it gives an equivalent ratio. For example, when the antecedent and the consequent of the ratio 1:3 are multiplied by 3, we get, (1 × 3) : (3 × 3) or 3 : 9. Here, 1 : 3 and 3 : 9 are equivalent ratios. Similarly, when both the terms of the ratio 20:10 are divided by 10, it gives 2 : 1. Here, 20 : 10 and 2 : 1 are equivalent ratios. An infinite number of equivalent ratios of any given ratio can be found by multiplying the antecedent and the consequent by a positive integer.
Ratio Table
A ratio table is a list containing the equivalent ratios of any given ratio in a structured manner. The following ratio table gives the relation between the ratio 1 : 4 and four of its equivalent ratios. The equivalent ratios are related to each other by the multiplication of a number. Equivalent ratios are obtained by multiplying or dividing the two terms of a ratio by the same number. In the example shown in the figure, let us take the ratio 1:4 and find four equivalent ratios, by multiplying both the terms of the ratio by 2, 3, 6, and 9. As a result, we get 2 : 8, 3 : 12, 6 : 24, and 9 : 36.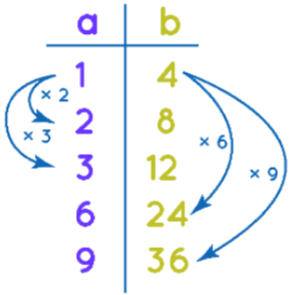
Example: There are 49 boys and 28 girls in a school auditorium. Express the ratio of the number of boys to that of girls.
Solution: Given, the number of boys = 49; and the number of girls = 28.
The GCF of 49 and 28 is 7. Now, to simplify, divide the two terms by their GCF which is 7.
This means, (49 ÷ 7)/(28 ÷ 7) = 7/4.
Therefore, the ratio of the number of boys to that of girls = 7 : 4.
|
185 videos|124 docs|75 tests
|
FAQs on What is Ratio? - Mathematics for Digital SAT
| 1. What is a ratio in mathematics? |  |
| 2. How do you simplify a ratio? |  |
| 3. What are some real-world examples of ratios? |  |
| 4. Can ratios be expressed in different forms? |  |
| 5. How can ratios be used to solve problems? |  |

|
Explore Courses for SAT exam
|

|

















