Statistics | Mathematics for ACT PDF Download

Introduction 

Statistics is a branch of mathematics that deals with the study of collecting, analyzing, interpreting, presenting, and organizing data in a particular manner. Statistics is defined as the process of collection of data, classifying data, representing the data for easy interpretation, and further analysis of data. Statistics also is referred to as arriving at conclusions from the sample data that is collected using surveys or experiments. Different sectors such as psychology, sociology, geology, probability, and so on also use statistics to function.

Mathematical Statistics

Statistics is used mainly to gain an understanding of the data and focus on various applications. Statistics is the process of collecting data, evaluating data, and summarizing it into a mathematical form. Initially, statistics were related to the science of the state where it was used in the collection and analysis of facts and data about a country such as its economy, population, etc. Mathematical statistics applies mathematical techniques like linear algebra, differential equations, mathematical analysis, and theories of probability.
There are two methods of analyzing data in mathematical statistics that are used on a large scale:

• Descriptive Statistics
• Inferential Statistics

Descriptive Statistics 
The descriptive method of statistics is used to describe the data collected and summarize the data and its properties using the measures of central tendencies and the measures of dispersion.

Inferential Statistics 
This method of statistics is used to draw conclusions from the data. Inferential statistics requires statistical tests performed on samples, and it draws conclusions by identifying the differences between the 2 groups. Tests calculate the p-value that is compared with the probability of chance(α) = 0.05. If the p-value is less than α, then it is concluded that the p-value is statistically significant.

Data Representation in Statistics

The collection of observations and facts is known a data. These observations and facts can be in the form of numbers, measurements, or statements. There are two different kinds of data i.e. Qualitative data and quantitative data. Qualitative data is when the data is descriptive or categorical and quantitative data is when the data is numerical information.
Once we know the data collection methods, we aim at representing the collected data in different forms of graphs such as a bar graph, line graph, pie chart, stem and leaf plots, scatter plot, and so on. Before the analysis of data, the outliers are removed that are due to the invariability in the measurements of data. Let us look at different kinds of data representation in statistics.

Different Models of Statistics

Statistics being a broad term used in various forms, different models of statistics are used in different forms. Listed below are a few models:

• Skewness: In statistics, the word skewness refers to a measure of the asymmetry in a probability distribution where it measures the deviation of the normal distribution curve for data. The value of skewed distribution could be positive or negative or zero. The curve is said to be skewed when it shifts from left to right. If the curve mores towards the right it is called a positive skewed and if the curve moves towards the left, it is called left-skewed.
• ANOVA Statistics: The word ANOVA means Analysis of Variance. The measure used in calculating the mean difference for the given set of data is called the ANOVA statistics. This model of statistics is used to compare the performance of stocks over a period of time.
• Degrees of freedom: This model of statistics is used when the values are changed. Data that can be moved while estimating a parameter is the degree of freedom.
• Regression Analysis: In this model, the statistical process determines the relationship between the variables. The process signifies how a dependent variable changes when an independent variable changed.

Measures of Central Tendency in Statistics

The measure of central tendency and the measure of dispersion are considered as the basis of descriptive statistics. The representative value for the given data is the measure of central tendency that gives us an idea of where data points are centered. This is done to find how the data are scattered around this centered measure. We use mean, median, and mode to find the central measures of tendency. In our day-to-day life, we find the average height of the students, the average income, the average score in exams, or of the player. The different measures of central tendency for the data are:

• Arithmetic Mean
• Median
• Mode
• Geometric Mean
• Harmonic Mean

Mean, Median and Mode in Statistics

Mean is considered the arithmetic average of a data set that is found by adding the numbers in a set and dividing by the number of observations in the data set. The middle number in the data set while listed in either ascending or descending order is the median. Lastly, the number that occurs the most in a data set and ranges between the highest and lowest value is the mode. For n number of observations, we have

• Mean = 
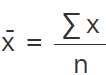
• Median = 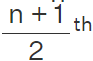  term if n is odd.
• Median =
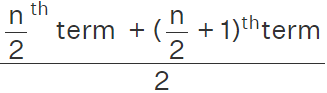
• Mode = The value which occurs most frequently

Measures of Dispersion in Statistics

The measures of central tendency do not suffice to describe the complete information about a given data. Thus we need to describe the variability by a value called the measure of dispersion. The different measures of dispersion are:

• The range in statistics is calculated as the difference between the maximum value and the minimum value of the data points.
• The quartile deviation that measures the absolute measure of dispersion. The data points are divided into 3 quarters. Find the median of the data points. The median of the data points to the left of this median is said to be the upper quartile and the median of the data points to the right of this median is said to be the lower quartile. Upper quartile - lower quartile is the interquartile range. Half of this is the quartile deviation.
• The mean deviation is the statistical measure to determine the average of the absolute difference between the items in a distribution and the mean or median of that series.
• The standard deviation is the measure of the amount of variation of a set of values.

Mean Deviation For ungrouped data

In statistics, the frequency distributions of data can be discrete data or continuous. For n number of individual observations
x₁, x₂, x₃, x_r, . . . . . x n x₁,x₂,x₃,x_r,.....x_n, the mean deviation about mean and median are calculated as follows:
Mean Deviation for ungrouped data = sum of deviation/number of observations =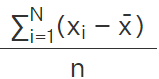

Mean Deviation for Discrete Grouped data

The measurements of the data units are clearly shown in such a frequency distribution. Let there be n distinct data points x₁, x₂, x₃, x_r , . . . . . x_n, occurring with frequencies f₁ , f₂ , f₃ . . . . f_n.

a) Mean deviation about mean

• We find the mean 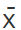 using 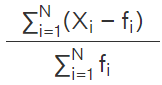 This is the ratio of the sum of the products of x_i observations and their respective frequencies f _i to the sum of the frequencies.
• Mean Deviation = 
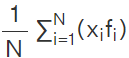
• After which find the deviations of observations x_i from the mean  and get their absolute values. i.e. 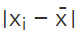 for all i = 1, 2, 3, .....n
• Mean Deviation =

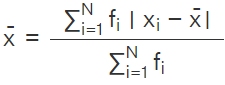
b) Mean deviation about median

• Find the median by arranging the observations in ascending order.
• Obtain the cumulative frequencies. Then identify the observation whose cumulative frequency is ≥ N/2, where N = sum of frequencies.
• Thus we have arrived at the required median. To get the absolute values of the deviations from median, we calculate MD( median) =
  

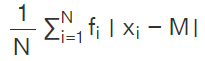
Mean Deviation for Continuous Grouped data

Here the data points take any value within a range and they are continuous. They can be measured and represented by using intervals on the real number line. The frequency in which data are arranged in classes is not countable.
a) Mean deviation about mean 
The mean of the continuous frequency distribution is centered at its mid-point in each class. Then the same procedure is followed as in the case of discrete frequency distribution.
b) Mean deviation about median
Median = 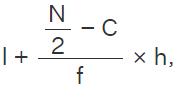  where the median class is the class interval whose cf is ≥ N/2, N the sum of frequencies, l, f, h, and C are, the lower limit, the frequency, the width of the median class and C the cumulative frequency of the class just preceding the median class. After finding the median, | x_i - M| is obtained.

Standard Deviation and Variance

We have the other prominent methods in statistics to find the proper measure of dispersion, known as the variance and the standard deviation. While finding the mean deviation about the mean and the median, there arises a difficulty in taking squares of all the deviations.

• If 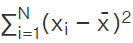 becomes zero, while calculating the sum for the mean, then it means there is no dispersion at all.
• If the sum is small, the observations are closer to the mean indicating a lower degree of dispersion.
• If the sum is large, there is a higher degree of dispersion of the observations from the mean .
• Thus this sum is a reasonable indicator of the degree of dispersion. This becomes the proper measure of dispersion, denoted as σ², and it is termed as the variance. Thus variance is given as σ² =
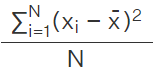
• The positive square root of the variance is called the standard deviation. σ =

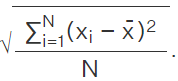
Coefficient of Variation

We compare the coefficient of variations of two or more frequency distributions. This coefficient of variation in statistics is the ratio of the standard deviation to the mean, expressed in percentage.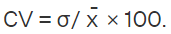

The distribution that has a greater coefficient of variation has more variability around the central value than the distribution having a smaller value of the coefficient of variation.

Important Notes

• The discipline of data collection and organization is called statistics. We interpret results based on the analysis done using the measures of central tendencies and the measures of dispersion.
• The frequency distribution of data is represented using bar graphs, histograms, pie charts, stem and leaf plots, line graphs, or ogives.
• The data collected can be either quantitative (numerical: discrete and continuous) or qualitative(categorical).