Rational Exponents

Rational exponents are exponents of numbers that are expressed as rational numbers, that is, in a^p/q, a is the base and p/q is the rational exponent where q ≠ 0. In rational exponents, the base must be a positive integer. Rules for rational exponents are similar to the rules of integer exponents. The numerator of a rational exponent represents the power whereas the denominator of a rational exponent represents the root.

What are Rational Exponents?

An exponential expression of the form a^m has a rational exponent if m is a rational number. In rational exponents, the powers and roots of a number are expressed together. Some of the examples of rational exponents are: 2^2/3, 9^5/9, 11^11/3, etc. Here the bases are positive integers and have rational exponents. Properties of general exponents also hold for the rational exponents.

Rational Exponents Definition

Rational exponents are defined as exponents that can be expressed in the form of p/q, where q ≠ 0. The general notation of rational exponents is x^m/n, where x is the base (positive number) and m/n is a rational exponent. Rational exponents can also be written as .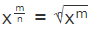

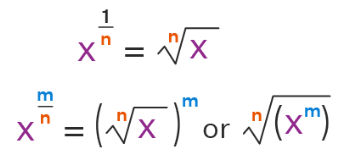
Rational Exponents Formulas

Now, let us go through some formulas of the rational exponents which are used to solve various algebraic problems. The formulas of integer exponents hold true for the rational exponents as well. Consider rational exponents with same bases a^m/n, a^p/q and a different base b^m/n

• a^m/n × a^p/q = a^{(m/n + p/q)}
• a^m/n ÷ a^p/q = a^{(m/n - p/q)}
• a^m/n × b^m/n = (ab)^m/n
• a^m/n ÷ b^m/n = (a÷b)^m/n
• a^-m/n = (1/a)^m/n
• a^0/n = a⁰ = 1
• (a^m/n)^p/q = a^{m/n × p/q}
• x^m/n = y ⇔ x = y^n/m

Rational Exponents and Radicals

We can write the rational exponents expressions as radicals by identifying the powers and roots and converting them into radicals. Consider the rational exponents' expression a^m/n. Now, follow the given steps:

• Step 1: Identify the power by looking at the numerator of the rational exponent. Here in rational exponent a^m/n, m is the power.
• Step 2: Identify the root by looking at the denominator of the rational exponent. Here in rational exponent a^m/n, n is the root.
• Step 3: Write the base as the radicand, power raising to the radicand, and the root as the index. Here we can write a^m/n = ⁿ√a^m.

We can convert radicals to rational exponents as well. Consider the square root of a positive number √a. We can write the square root √a as a rational exponent. √a = a^1/2 which is a rational exponent. 

Simplifying Rational Exponents

Now, that we have studied the formulas of rational exponents and how to write rational exponents as radicals, let us solve some problems to learn how to simplify rational exponents. To simplify rational exponents, we need to reduce the exponential expression to its simplest form.
Example: Simplify the rational exponent 64^2/3
Solution: We can write 64^2/3 as 64^2/3 = (³√64)² or 64^2/3 = ³√(64)²
It is easier to determine the cube root of 64 and then squaring it as compared to finding the square of 64 and then finding its cube root. To simplify the rational exponent 64^2/3, we have 
64^2/3 = (³√64)²
⇒ 64^2/3 = (4)²
⇒ 64^2/3 = 16
Hence the rational exponent 64^2/3 is simplified to 16.

Non-Integer Rational Exponents

Exponents with fractions and decimals are referred to as non-integer rational exponents. The general format of a rational exponent is: a^p/q.
Here 'a' is the base and the rational number, p/q is the exponent. Observe the following examples of non integer rational exponents. 2^0.5, 5^2/3, 11^1/2.
Consider 27^2/3, where 2/3 is the non integer rational exponent. It can also be written in the radical form as: ³√(27)² = (³√27)²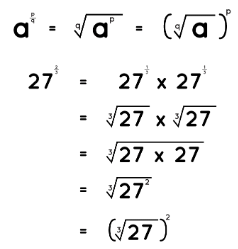

How to Simplify Non-Integer Rational Exponents?

The non-integer rational exponents can be solved in the same way by which the exponents with integers are solved. Let us recall that if 'a' is the base and 'm' and 'n' are the exponents, which are non zero integers, the following exponent rules are used to solve the exponents.

• a^m × aⁿ = a^m+n
• a^m / aⁿ = a^m-n
• (a^m)ⁿ = a^{m × n}
• a^{- m} = 1/a^m
• 

Observe the following examples which show how the same exponential laws are used to solve the fractional exponents as well.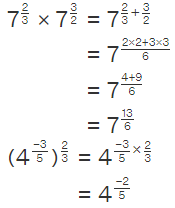

Tips and Tricks on Rational Exponents

• a^m/n = ⁿ√a^m
• a^1/m × a^1/n = a^{(1/m + 1/n)}
• a^1/m ÷ a^1/n = a^{(1/m - 1/n)}
• a^1/m × b^1/m = (ab)^1/m
• a^1/m ÷ b^1/m = (a÷b)^1/m
• (a^m)^1/n = a^m/n