Radical | The Complete SAT Course - Class 10 PDF Download
In maths, a radical is the opposite of an exponent that is represented with a symbol '√' also known as root. It can either be a square root or a cube root and the number before the symbol or radical is considered to be an index number or degree. This number is a whole number represented as an exponent that cancels out the radical.
What is Radical?
The radical of a number is the same as the root of a number. The root can be a square root, cube root, or in general, nth root. Thus, any number or expression that uses a root is known as a radical. The term radical is derived from the Latin word Radix which means root. The radical can describe different kinds of roots for a number such as square root, cube root, fourth root, and so on. The number written before the radical is known as the index number or degree. This number helps in telling us how many times the number would be multiplied by itself to equal the radicand. This is considered to be the opposite of an exponent just like addition being the opposite of subtraction and division being the opposite of multiplication. For example: ∛125 = 5 as 5 × 5 × 5 = 125.
Radical Definition
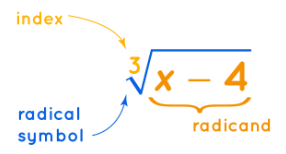
The symbol '√' that expresses a root of a number is known as radical and is read as x radical n or nth root of x. The horizontal line covering the number is called the vinculum and the number under it is called the radicand. The number n written before the radical is called the index or degree. Some examples of radicals are √7, √2y+1, etc.
A radical can also be associated with the following terms:
- An equation that is inside a radical is known as a radical equation.
- An expression that lies inside a square root is known as a radical expression.
- An inequation that is inside a radical is known as radical inequality.
Radical General Rules
Mentioned below are a few general rules for a radical.
- If the number is positive under the radical, the result will be positive.
- If the number is negative under the radical, the result will be negative.
- If the number under the radical is negative and an index is an even number, the result will be an irrational number.
- If an index is not mentioned, the radical will be square root.
- Multiplication of numbers under the same radical and index is possible. For example, ∛12 × ∛10 = ∛120.
- Division is possible for numbers under the same radical. For example, √8/√4 = √8/4 = √2.
- The reverse of the multiplication rule is possible, where the number is split under the same radical. For example, √27 = √9 × √3 = ∛3 × √3.
- The radical can be written in its exponent form as well in any equation. For example, √x = 25 (√x)2 = (25)2 x = 5.
- The inverse exponent of the index number is equivalent to the radical itself. For example, √7 = (7)1/2.
Radical Formula
To solve a radical equation, it has to be made radical-free. To make an equation of nth root radical free, we power both sides of the equation with 'n'. This masked the radical equation-free from radical. Let's look into the radical formula below.
n√ x=p
x1/n = p
(x1/n)n = pn
x = pn
where,
- The n√ symbol is known as the radical of nth root.
- 'n' is known as the index.
- The expression or variable inside the radical symbol i.e, x is known as the radicand.
|
433 videos|220 docs|166 tests
|
















