Introduction to Motion in a Straight Line | Science for ACT PDF Download

Motion in a Straight Line can be seen in many areas of our everyday life. A lift moving up and down, the scouts doing a parade march are all examples of straight-line motion. The study of motion is called Mechanics. Mechanics is one of the earliest branches of Physics. An Engineering or Architecture aspirant must pay attention to this branch of physics as they form the core of your graduate studies.

What is Motion?

Before we begin Motion in a Straight Line notes, let’s first understand ‘what is motion’?. In our daily life, we are surrounded by moving objects. For example: Walking on the streets, a running boy, a car moving on a road, moving planes, etc. The above movements of the objects are examples of motion.
Motion: The change in the position of any object with respect to time is called motion.
Kinematics: The study of the motion of an object without knowing its cause is called kinematics.

Types of Motion

A car moving on a road, a runner doing laps, and the to and fro movement of swings are all examples of motion. Yet all these movements are of different types. So, depending on the path followed by the moving object Motion can be classified into:

• Rectilinear Motion: Motion in a straight line or linear motion.
• Rotational Motion: Motion along a circular path.
• Vibration Motion: Vibration of a body along a fixed axis.
• Oscillation Motion: To and from motion of a body.

In this article, we are going to study the basics of Linear or Rectilinear Motion in detail. Before we learn about motion, let’s have a look at the parameters of motion.

Position, Path Length or Distance and Displacement in a Straight Line

• Have you ever travelled to a friend’s house from your place? How do you determine the distance, direction, and time required? If you ask for directions from your friend, they will probably guide you on how to follow the left and right turns, up and down walks to his or her place. Just like that, in physics, instead of right and left, up and down we have two coordinate axes namely X-axis and Y-axis, and positive and negative signs to determine the direction.
• If you want to measure the distance between your house and your friend’s place then you will consider your house to be the datum i.e. at 0. In physics, we have represented this as the origin. And your friend’s house will be represented by a set of coordinates (x,y) from the origin.
• The use of left and right can be confusing. It depends on the orientation of the person. Also, it depends on the external parameters. For example, “Take a right from the lamp post.” To do this you have to depend on the lamp post as a reference. The directions of North, South, East and West also can be read with the help of a compass that in turn depends on the earth’s magnetic field. So, how can one find the locations in space?
• This is the significance of the use of the coordinate system. The use of coordinates makes the physical system Universal. It can be easily read and understood by anyone. Unlike the directions right and left the coordinate system is independent of external parameters. It only depends on the origin and axes.
• Motion: If anyone coordinates the object change with respect to time then we say that the object is in motion. Or the change in position of the object with respect to time is called motion.
• Rest: If no coordinates of the object with respect to the coordinate system change with respect to time then the object is said to be at rest.
• You can also check details about Vector.

What is the Position of An Object?

The location of an object with respect to a reference point or origin is called the position of that object. The intersection point of the X-axis and Y-axis is called origin (O). The origin is generally taken as a reference point to find the position of any object.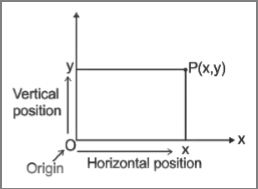

Here the coordinates P(x, y) denotes the position of point P with respect to the origin. To describe the motion of any object in one dimension we can choose any one axis (generally we take the X-axis).

Position-time graph

For a stationary object: Here the object is at rest so the position (x) of the object is not changing with respect to time (t) which is equal to x always.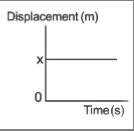

For a uniform motion: Here the object is covering an equal distance in an equal time interval. The graph of position (x) – time (t) will be a straight line passing through the origin.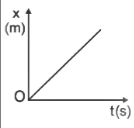 

What is Path Length or Distance?

The total distance travelled by an object from a starting point is called path length. Thus the total path length of an object is called the distance travelled by that object.

What is Displacement?

The minimum path length between the starting point to the final point is called displacement.
The SI unit of displacement is the metre (m) and the CGS unit of displacement is centimetre (cm). Speed and Velocity
Distance over time gives Speed. Similarly, Displacement over time gives Velocity.
Speed = slope of a distance-time graph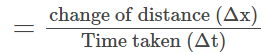 

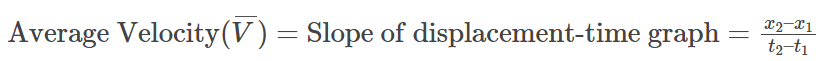
Types of Linear Motion

Based on the nature of displacement, linear motion is classified as

Uniform Motion in Straight Line

When an object is travelling an equal distance in equal time intervals then this type of motion is called uniform motion. Or when the velocity of the object is constant throughout the motion is called uniform motion.
Examples of Uniform Motion:

1. The motion of the parade.
2. The motion of a train at a constant speed

Non-Uniform Motion in Straight Line

When an object is travelling an unequal distance in unequal time intervals then this type of motion is called non-uniform motion.
Examples of Non-Uniform Motion:

1. Movement of an asteroid
2. A bouncing ball
3. A car coming to halt

Points to Remember for Uniform and Non-Uniform Motion

• For uniform motion, the instantaneous velocity of the particle is equal to the average velocity of the particle.
• The velocity or instantaneous velocity is the same for any particle.
• The slope of the displacement-time graph gives the velocity. The slope of a graph can be positive, negative or zero. So the velocity also can be positive, negative or zero respectively. But for the speed, we take the magnitude of the slope, so the speed is always positive.

Uniform Speed and Uniform Velocity in Straight Line

• Uniform Speed: When the speed of an object does not change then it is travelling at a uniform speed. 
• Uniform Velocity: When an object with uniform speed travelling without changing its direction then it is said to have uniform velocity.

Variable Speed and Variable Velocity in Straight Line

• Variable Speed: A body covering covers unequal distances in equal intervals of time is said to be moving with a variable speed.
• Variable Velocity: A body covering unequal distances in equal intervals of time in a specified direction is said to be moving with a variable velocity.

Average Speed and Average Velocity in Straight Line

• Average Speed: Average speed is the arithmetic mean value of the speed of a body over a period of time.
• Average Velocity: Average velocity is the arithmetic mean value of the velocity of a body over a period of time.

What is Acceleration?

• The rate of change in velocity is called acceleration. It is a vector quantity. The acceleration is denoted by ‘a’.
• The SI unit of acceleration is m/s² and the CGS unit is cm/s².
• The slope of the velocity-time graph gives the acceleration.
  
• The change of velocity divided by the total time taken is called the average acceleration of the particle.
  
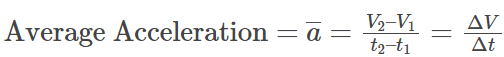
• The rate of change of velocity at a particular instant of time is called the instantaneous acceleration of the particle.
  
  As dV = a dt
  

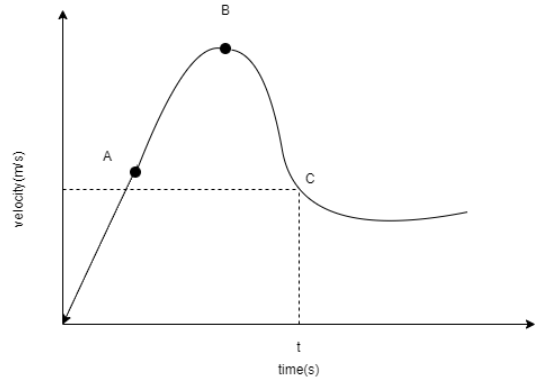
In this graph, average acceleration between points A and B can be given by,

And Instantaneous acceleration at point C becomes,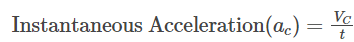 

Thus the area under the acceleration –time graph gives the change in velocity of the particle.

Practice Problems on Acceleration

Q. The velocity of a particle varies as V = 2t²+3t. Then find the acceleration of the particle after time t = 2 sec.
Ans. Given that: V = 2t²+3t
Acceleration is given by: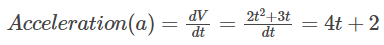

After time t = 2 sec
Acceleration (a) = 4 × 2 + 3 = 11 m/s²

Kinematic Equations for Uniformly Accelerated Motion in a Straight Line

There are three equations of motions: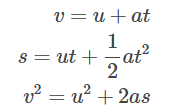

Where V is final velocity, u is initial velocity, S is displacement, a is acceleration and t is the time taken.

Relative Velocity in Straight Line

The velocity of a moving object with respect to another moving object is called relative velocity.
Let velocity of A is V_A and velocity of B is V_B then relative velocity of A with respect to B is given by:
V_AB=V_A–V_B
And the relative velocity of B with respect to A is given by:
V_BA=V_B–V_A
Thus V_AB =–V_BA
Similarly, the relative acceleration of A with respect to B is given by:
Here a_AB = Acceleration of A (a_A) – acceleration of B (a_B)

Q. A man A sitting in a train which is moving at 80 km/h is observing a running man B on the platform in the opposite direction to the train movement. Find the velocity of the man on the platform with respect to the man on the train. The velocity of man on the platform is 20 km/hr.
Ans. 
Given that: Velocity of man A (V_A) = velocity of train = 80 km/hr
Man B is moving opposite to the train, so we will take the velocity of man B as negative.
Velocity of man B (V_B) = – 20 km/hr
Velocity of man B with respect to man A = V_AB = V_A – V_B = – 20 – 80 = – 100 km/hr
The negative sign shows the opposite direction of velocity.