Vector Space | Engineering Mathematics - Engineering Mathematics PDF Download
| Table of contents |

|
| Introduction |

|
| Definition |

|
| Vector Space Axioms |

|
| Vector Space Properties |

|
| Vector Space Problems |

|
Introduction
A vector space, also known as a linear space, is a collection of objects called vectors. Vectors can be combined through addition and scaled by numbers, typically real numbers, known as scalars. However, in some instances, scalar multiplication can involve rational numbers, complex numbers, and other numeric types. The operations of vector addition and scalar multiplication must adhere to specific mathematical rules, often referred to as axioms. Real vector spaces and complex vector spaces are terms used to denote the use of real or complex numbers as scalars in these spaces.
Definition
A vector space, characterized by the presence of vectors, adheres to specific mathematical properties related to vector addition and scalar multiplication. These properties include the associative and commutative laws for vector addition and the associative and distributive rules for scalar multiplication.
In a vector space, you'll find the following components:
- A set V, with its elements referred to as vectors.
- A field F, with its elements representing scalars.
- Two fundamental operations: a. Vector addition, taking two vectors u and v from V to produce a third vector u + v, which also belongs to V. b. Scalar multiplication, involving a scalar c from F and a vector v from V to generate a new vector cv within V.
Both vector addition and scalar multiplication operations must meet specific conditions. These conditions are outlined in axioms, which extend the properties of vectors found within the field F. When a vector space is defined over the real numbers (R), it is termed a real vector space, while over the complex numbers (C), it is known as a complex vector space.
What distinguishes a Vector from a Vector Space?
A vector is a constituent element of a vector space. On the other hand, a vector space is a collection of objects that can be scaled by scalars and subjected to vector space axioms.
Is zero considered a vector space?
Indeed, zero qualifies as a vector space, known as the trivial vector space, denoted by {0}. This space contains the zero vector or null vector, and in this scenario, vector addition and scalar multiplication are straightforward and minimal.
Defining Equal Vectors
Equal vectors are vectors that share both the same magnitude and the same direction. When two vectors are considered equal, it means the line segments they represent are parallel, and their vector columns exhibit identical characteristics.
Vector Space Axioms
All the axioms should be universally quantified. For vector addition and scalar multiplication, it should obey some of the axioms. Here eight axiom rules are given.
Conditions for Vector Addition
An operation vector addition ‘ + ‘ must satisfy the following conditions:
Closure : If x and y are any vectors in the vector space V, then x + y belongs to V
- Commutative Law : For all vectors x and y in V, then x + y = y + x
- Associative Law : For all vectors x, y and z in V, then x + (y + z) = (x + y) + z
- Additive Identity : For any vector x in V, the vector space contains the additive identity element and it is denoted by ‘ 0 ‘ such that 0 + x = x and x + 0 = x
- Additive inverse : For each vector x in V, there is an additive inverse -x to get a solution in V.
Condition for Scalar Multiplication
An operation scalar multiplication is defined between a scalar and a vector and it should satisfy the following condition :
Closure: If x is any vector and c is any real number in the vector space V, then x. c belongs to V
- Associative Law: For all real numbers c and d, and the vector x in V, then c. (d. v) = (c . d). v
- Distributive law: For all real numbers c and d, and the vector x in V, (c + d).v = c.v + c.d
- Distributive law: For all real numbers c and the vectors x and y in V, c.(x + y) = c. x + c. y
- Unitary Law : For all vectors x in V, then 1.v = v.1 = v
Vector Space Properties
Here are some basic properties that are derived from the axioms are
- The addition operation of a finite list of vectors v1 v2, . . , vk can be calculated in any order, then the solution of the addition process will be the same.
- If x + y = 0, then the value should be y = −x.
- The negation of 0 is 0. This means that the value of −0 = 0.
- The negation or the negative value of the negation of a vector is the vector itself: −(−v) = v.
- If x + y = x, if and only if y = 0. Therefore, 0 is the only vector that behaves like 0.
- The product of any vector with zero times gives the zero vector. 0 x y = 0 for every vector in y.
- For every real number c, any scalar times of the zero vector is the zero vector. c0 = 0
- If the value cx= 0, then either c = 0 or x = 0. The product of a scalar and a vector is equal to when either scalar is 0 or a vector is 0.
- The scalar value −1 times a vector is the negation of the vector: (−1)x = −x. We define subtraction in terms of addition by defining x − y as an abbreviation for x + (−y).
x − y = x + (−y)
All the normal properties of subtraction follow:
- x + y = z then the value x = z − y.
- c(x − y) = cx − cy.
- (c − d)x = cx − dx
Vector Space Problems
Go through the vector space problem provided here.
Question : Show that each of the conditions provided is in vector space
- The set of linear polynomials
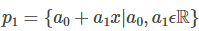 under the addition and scalar multiplication operations.
under the addition and scalar multiplication operations. - Under usual matrix operation, the set of 2 x 2 matrix with real entries
- Three component row vectors with usual operations
- The set
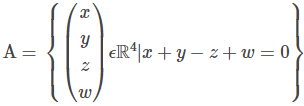 under the operations from R4
under the operations from R4
Solution: Conditions checked from the axioms and properties:
- The zero element is 0 + 0x is zero
- The zero element of the vector space under 2 x 2 matrix is zero
- The zero element of three component row vectors are zeros
- The closure property of addition involves
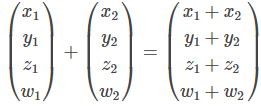
is in A because
(x1+x2) + (y1+y2) – (z1+z2) + (w1+w2) = ( x1+y1-z1+w1)+(x2+y2-z2+w2) = 0 + 0
Similarly, the closure of scalar multiplication can be obtained.
|
65 videos|129 docs|94 tests
|
FAQs on Vector Space - Engineering Mathematics - Engineering Mathematics
| 1. What is a vector space? |  |
| 2. What are the key properties of a vector space? |  |
| 3. How do vector spaces relate to linear algebra? |  |
| 4. What is the dimension of a vector space? |  |
| 5. Can a vector space contain an infinite number of vectors? |  |





















