What are Domain and Range? | The Complete SAT Course - Class 10 PDF Download
Introduction
The domain and range are defined for a relation and they are the sets of all the x-coordinates and all the y-coordinates of ordered pairs respectively. For example, if the relation is, R = {(1, 2), (2, 2), (3, 3), (4, 3)}, then:
- Domain = the set of all x-coordinates = {1, 2, 3, 4}
- Range = the set of all y-coordinates = {2, 3}
We can visualize this here: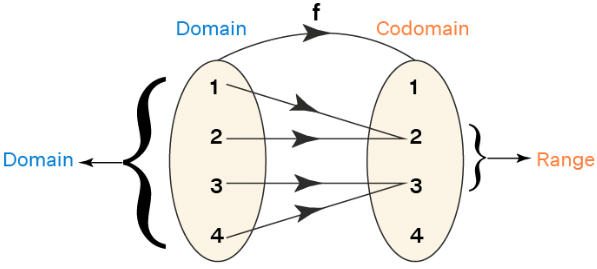
Domain and Range of a Function
- The domain and range of a function are the components of a function. The domain is the set of all the input values of a function and range is the possible output given by the function. Domain→ Function →Range. If there exists a function f: A →B such that every element of A is mapped to elements in B, then A is the domain and B is the co-domain.
- The image of an element 'a' under a relation R is given by 'b', where (a,b) ∈ R. The range of the function is the set of images. The domain and range of a function is denoted in general as follows: Domain(f) = {x ∈ R} and range(f)={f(x) : x ∈ domain(f)}
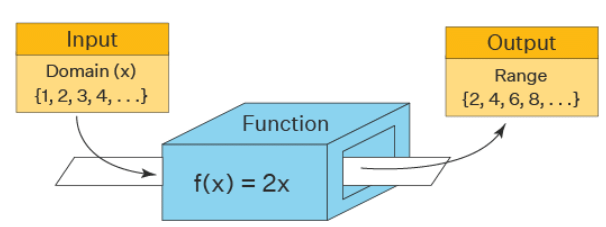
Domain and Range of a Function
- The domain and range of this function f(x) = 2x is given as domain D ={x ∈ N } , range R = {(y): y = 2x}
Domain of a Function
- A domain of a function refers to "all the values" that go into a function. The domain of a function is the set of all possible inputs for the function. Consider this box as a function f(x) = 2x . Inputting the values x = {1,2,3,4,...}, the domain is simply the set of natural numbers and the output values are called the range. But in general, f(x) = 2x is defined for all real values of x and hence its domain is the set of all real numbers which is denoted by (-∞, ∞). Here are the general formulas used to find the domain of different types of functions. Here, R is the set of all real numbers.
- Domain of any polynomial (linear, quadratic, cubic, etc) function is R.
- Domain of a square root function √x is x≥0.
- Domain of an exponential function is R.
- Domain of logarithmic function is x > 0.
- To find the domain of a rational function y = f(x), set the denominator ≠ 0.
Range of a Function
- The range of a function is the set of all its outputs. Example: Let us consider the function f: A→ B, where f(x) = 2x and each of A and B = {set of natural numbers}. Here we say A is the domain and B is the co-domain. Then the output of this function becomes the range. The range = {set of even natural numbers}. The elements of the domain are called pre-images and the elements of the co-domain which are mapped are called the images.
- Here, the range of the function f is the set of all images of the elements of the domain (or) the set of all the outputs of the function. In the upcoming sections, we can see how to find the range of different types of functions. Here are the general formulas used to find the range of different types of functions. Note that R is the set of all real numbers here.
- Range of a linear function is R.
- Range of a quadratic function y = a(x-h)2 + k is:
- y≥k, if a>0 and
- y≤k, if a<0
- Range of a square root function is y≥0.
- Range of an exponential function is y>0.
- Range of logarithmic function is R.
- To find the range of a rational function y = f(x), solve it for x and set the denominator ≠ 0.
How To Calculate Domain And Range?
- Suppose X = {1, 2, 3, 4, 5}, f: X → Y, where R = {(x,y) : y = x+1}.
- Domain = the input values. Thus Domain = X = {1, 2, 3, 4, 5}
- Range = the output values of the function = {2, 3, 4, 5, 6}
- and the co-domain = Y = {2, 3, 4, 5, 6}
Domain and Range of Exponential Functions
- The function y = ax, a ≥ 0 is defined for all real numbers. Hence, the domain of the exponential function is the entire real line. The exponential function always results in a positive value. Thus, the range of the exponential function is of the form y= |ax+b| is y ∈ R , {y > 0}. Domain = R, Range = (0, ∞)
Example: Look at the graph of this function f: 2x
Domain and range of a function 2x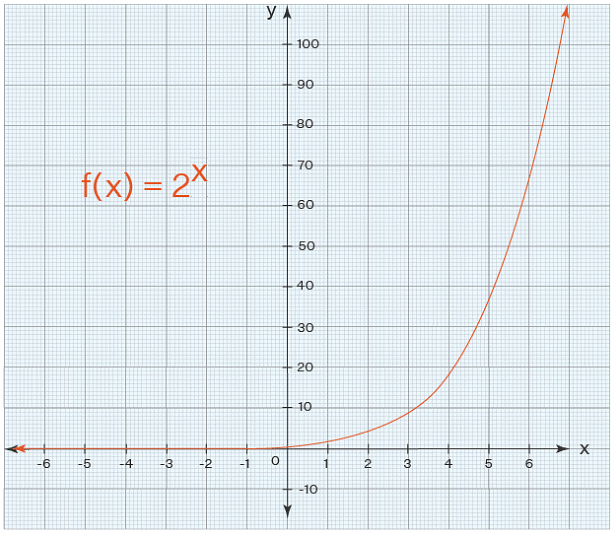
Observe that the value of the function is closer to 0 as x tends to ∞ but it will never attain the value 0. The domain and range of an exponential functions are given as follows:
- Domain: The domain of the function is the set R.
- Range: The exponential function always results in positive real values.
Domain and Range of Trigonometric Functions
Look at the graph of the sine function and cosine function. Notice that the value of the functions oscillates between -1 and 1 and it is defined for all real numbers.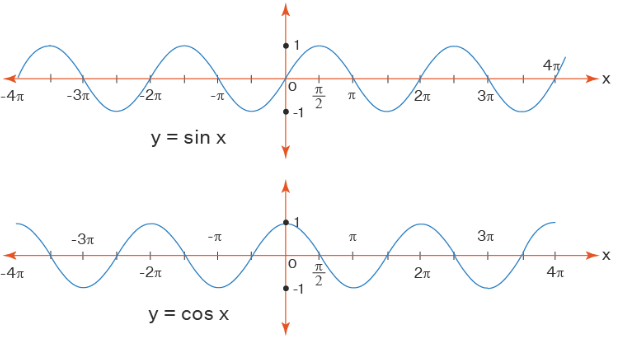
Thus, for each of the sine and cosine functions:
- Domain: The domain of the functions is the set R.
- Range: The range of the functions is [-1, 1]
The domain and range of all trigonometric functions are shown below:
Domain and Range of an Absolute Value Function
The function y=|ax+b| is defined for all real numbers. So, the domain of the absolute value function is the set of all real numbers. The absolute value of a number always results in a non-negative value. Thus, the range of an absolute value function of the form y= |ax+b| is y ∈ R | y ≥ 0. The domain and range of an absolute value function are given as follows
- Domain = R
- Range = [0, ∞)
Example: |6-x|
- Domain: The domain of the function is the set R.
- Range: We already know that the absolute value function results in a non-negative value always. i.e., |6-x| ≥ 0, for all x.
Domain and Range of a Square Root Function
- The function y= √(ax+b) is defined only for x ≥ -b/a
- So, the domain of the square root function is the set of all real numbers greater than or equal to -b/a. We know that the square root of something always results in a non-negative value. Thus, the range of a square root function is the set of all non-negative real numbers. The domain and range of a square root function are given as: Domain = [-b/a,∞), Range = [0,∞)
Example: y= 2- √(-3x+2)
- Domain: A square root function is defined only when the value inside it is a non-negative number. So for a domain,
-3x+2 ≥ 0
-3x ≥ -2
x ≤ 2/3 - Range: We already know that the square root function results in a non-negative value always.
√(-3x+2)≥ 0
Multiply -1 on both sides
-√(-3x+2) ≤ 0
Adding 2 on both sides
2-√(-3x+2)≤ 2
y≤ 2
Graphs of Domain and Range
- Another way to identify the domain and range of functions is by using graphs. The domain refers to the set of possible input values. The domain of a graph consists of all the input values shown on the x-axis. The range is the set of possible output values shown on the y-axis. The easiest method to find the range of function is by graphing it and looking for the y-values covered by the graph.
- To find the range of a quadratic function, it is sufficient to see if it has a maximum or minimum value. The maximum/minimum value of a quadratic function is the y-coordinate of its vertex. To find the domain of the rational function, set the denominator as 0 and solve for the variable. The domain is denoted by all the values from left to right along the x-axis and the range is given by the span of the graph from the top to the bottom.

Graph of Domain and range of functions
Domain and Range From Graph
- It is very easy to find the domain and range of a function if its graph is given/known. The set of values of x covered by the graph gives the domain and the set of values of y covered by the graph gives the range. But keep a note of the following things while writing the domain and range from a graph.
- See whether the graph passes the vertical line test. Otherwise, it is not a function and we do not usually define domain and range for such curves.
- If there is any hole on the graph, then its coordinates shouldn't be in the domain and range.
- If there is a vertical asymptote, then the corresponding value of x shouldn't be there in the domain.
- If there is a horizontal asymptote, then the corresponding value of x shouldn't be there in the range.
- If the graph is broken into pieces, then we get multiple sets/intervals in the domain and range and we club all such sets/intervals by "union" symbol (∪).
- If there is an arrow at the end of a curve, then it means that the curve is supposed to be extended infinitely in that particular direction.
Here is an example of a graph and we will find the domain and range from the graph.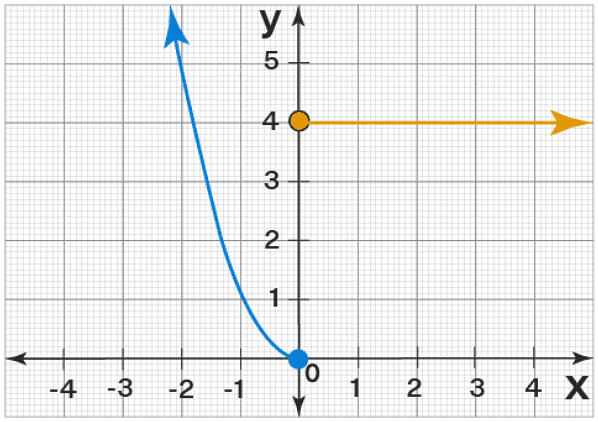
In the above graph:
- All the x-values from -∞ to ∞ are covered by the graph (because of arrows, the two curves extend infinitely in the given directions). Hence, the domain = (-∞, ∞).
- All the y-values greater than or equal than or equal to 0 are covered by the graph (see there is no part of the curve that is below the y-axis). Hence, the range = [0, ∞).
Important Notes on Domain and Range:
- The domain and range of function is the set of all possible inputs and outputs of a function respectively.
- The domain and range of a function y = f(x) is given as domain= {x, x∈R }, range= {f(x), x∈Domain}.
- The domain and range of any function can be found algebraically or graphically.
Examples on Domain and Range
Example 1. Find the domain and range of the real function f defined by f(x) = √(x-1)
Given the function is real. Thus the domain and range of the function are also real.
The minimum value it could take is 1 and the maximum value is ∞. Thus domain = [1, ∞).
Since f(x) is always non-negative, the minimum value of the range is 0 and it can range up to infinity. Thus range = [0, ∞)
The domain and the range of the function f defined by f(x) = √(x-1) is domain = [1, ∞) and range = [0, ∞)
Example 2: Find the domain and range of the function (x+1)/(3-x).
At first, we will set the denominator equal to 0, and then we will solve for x.
3 - x = 0
- x = - 3 ⇒ x = 3
Hence, we will exclude 3 from the domain.
So, the domain is the set of real numbers x, where (x< 3) and (x > 3)
Let's find the range of y = (x+1)/(3-x)
Let us solve the given equation for x
(3 - x)y = x + 1
3y - xy = x + 1
3y-1 = x + xy
x(1 + y) = 3y - 1
x = (3y - 1)/(1 + y)
The final equation is a fraction and a fraction is NOT defined when its denominator is zero.
So 1+y ≠ 0 ⇒ y≠ -1
Therefore, the range of the given function is the set of all real numbers excluding -1
Domain = (-∞,3) ∪ (3, ∞), Range = (-∞,-1) ∪ (-1, ∞)
The domain and range of the function (x+1)/(3-x): Domain = (-∞,3) ∪ (3, ∞), Range = (-∞,-1) ∪ (-1, ∞)
|
405 videos|217 docs|164 tests
|
















