One to One Function | The Complete SAT Course - Class 10 PDF Download
What is a One to One Function?
A normal function can actually have two different input values that can produce the same answer, whereas a one to one function does not. Let’s go ahead and start with the definition and properties of one to one functions.
One to One Function Definition
- One to one function is a special function that maps every element of the range to exactly one element of its domain i.e, the outputs never repeat. As an example, the function g(x) = x - 4 is a one to one function since it produces a different answer for every input. Also, the function g(x) = x2 is NOT a one to one function since it produces 4 as the answer when the inputs are 2 and -2. A function that is not one-to-one is called a many-to-one function.
Algebraically, we can define one to one function as:
function g: D -> F is said to be one-to-one if
- g(x1) = g(x2) ⇒ x1 = x2
for all elements x1 and x2 ∈ D. A one to one function is also considered as an injection, i.e., a function is injective only if it is one-to-one. The contrapositive of this definition is a function g: D -> F is one-to-one if x1 ≠ x2 ⇒ g(x1) ≠ g(x2). Let us visualize this by mapping two pairs of values to compare functions that are and that are not one to one.
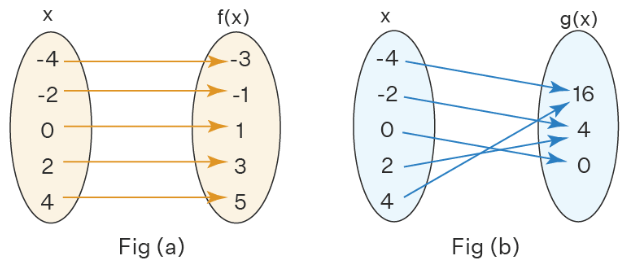
- In the Fig (a) (which is one to one), x is the domain and f(x) is the codomain, likewise in Fig (b) (which is not one to one), x is a domain and g(x) is a codomain.
- In Fig(a), for each x value, there is only one unique value of f(x) and thus, f(x) is one to one function.
- In Fig (b), different values of x, 2, and -2 are mapped with a common g(x) value 4 and (also, the different x values -4 and 4 are mapped to a common value 16). Thus, g(x) is a function that is not a one to one function.
Horizontal Line Test
The horizontal line test is used to determine whether a function is one-one when its graph is given. We have already seen the condition (g(x1) = g(x2) ⇒ x1 = x2) to determine whether a function g(x) is one-one algebraically. On the other hand, to test whether the function is one-one from its graph,
- just take a horizontal line (consider a horizontal stick) and make it pass through the graph.
- If the horizontal line is NOT passing through more than one point of the graph at any point in time, then the function is one-one.
- If the horizontal line passes through more than one point of the graph at some instance, then the function is NOT one-one.
Example: Consider the graph below.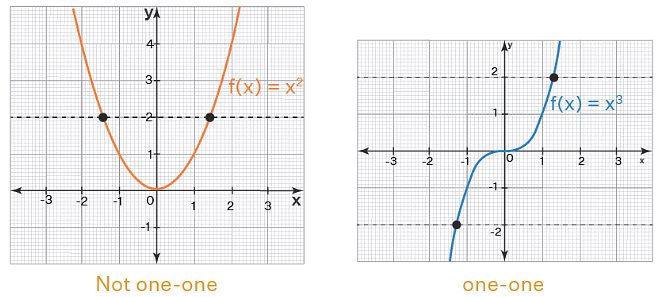
In the above graph,
- f(x) = x2 (which is a quadratic function) is NOT one-one as it failed the horizontal line test (as the horizontal line passes through more than one point of the graph)
- f(x) = x3 (which is a cubic function) is one-one as it passed the horizontal line test (as the horizontal line passes through only one point of the graph every time)
Properties of One to One Function
A one-to-one function i.e an injective function that maps the distinct elements of its domain to the distinct elements of its co-domain. Here are some properties that help us to understand the various characteristics of one to one functions:
- If two functions, f(x) and k(x), are one to one, the composite function f ◦ k is a one to one function as well. (f ◦ k) (x1) = (f ◦ k) (x2) ⇒ f(k(x1)) = f(k(x2)) ⇒ k(x1) = k(x2) ⇒ x1 = x2
- The domain of the function g equals the range of g-1 and the range of g equals the domain of g-1
- If a function is considered to be one to one, then its graph will either be always increasing or always decreasing.
- g-1 (g(x)) = x, for every x in the domain of g, and g(g-1(x)) = x for every x in the domain of g-1.
- If f ◦ k is a one to one function, then k(x) is also guaranteed to be a one to one function
- The graph of a function and the graph of its inverse are symmetric with each other with respect to the line y = x.
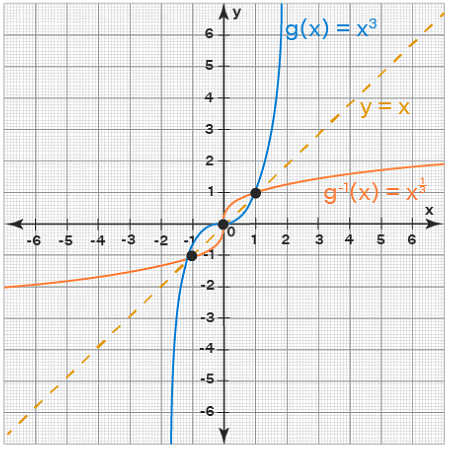
One to One Function and Inverse Function
How to Determine if a Function is One to One?
Vertical line test are used to determine if a given relation is a function or not. Further, we can determine if a function is one to one by using two methods:
- Testing one to one function graphically: If the graph of g(x) passes through a unique value of y every time, then the function is said to be one to one function (horizontal line test).
- Testing one to one function algebraically: The function g is said to be one to one if a = b for every g(a) = g(b)
- Testing one to one function using derivatives: A function g(x) is said to be one-one if and only if either g'(x) > 0 or g'(x) < 0 throughout the domain. i.e., if a function is either increasing or decreasing throughout, then it is one-one. For example, the exponential function f(x) = ex is completely an increasing function throughout its domain (-∞, ∞) and hence it is one-one. Graph it once and check.
One to One Function Graph
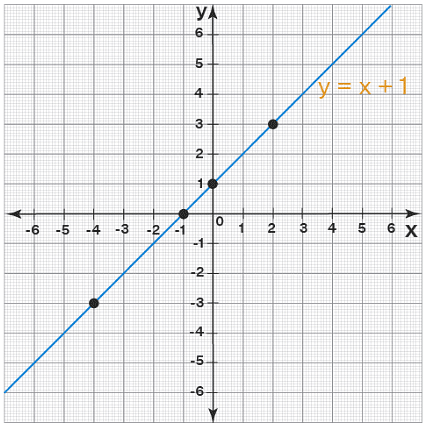
- Any function can be represented in the form of a graph. This function is represented by drawing a line/a curve on a plane as per the cartesian sytem. The domain is marked horizontally with reference to the x-axis and the range is marked vertically in the direction of the y-axis. If a function g is one to one function then no two points (x1, y1) and (x2, y2) have the same y-value.
- Therefore no horizontal line cuts the graph of the equation y = g(x) more than once. The following figure (the graph of the straight line y = x + 1) shows a one-one function. Note that no two points on it have the same y-coordinate (or) it passes the horizontal line test.
Inverse of One to One Function
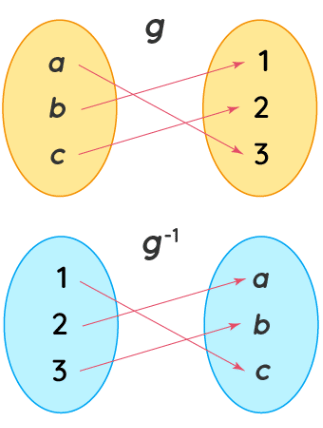
- It is essential for one to understand the concept of one-to-one functions in order to understand the concept of inverse functions and to solve certain types of equations. Firstly, a function g has an inverse function, g-1, if and only if g is one to one. In the below-given image, the inverse of a one-to-one function g is denoted by g−1, where the ordered pairs of g-1 are obtained by interchanging the coordinates in each ordered pair of g. Here the domain of g becomes the range of g-1, and the range of g becomes the domain of g-1.
Properties of the Inverse of One to One Function
The inverse of one to one function undoes what the original function did to a value in its domain in order to get back to the original y-value. Here are the properties of the inverse of one to one function:
- The function f has an inverse function if and only if f is a one to one function i.e, only one-to-one functions can have inverses.
- If the functions g and f are inverses of each other then, both these functions can be considered as one to one functions.
- If f and g are inverses of each other if and only if (f ◦ g) (x) = x, x in the domain of g and (g ◦ f) (x) = x, x in the domain of f. Here f ◦ g is the composition function that has 'f' composed with 'g'. '
- If f and g are inverses of each other then the domain of f is equal to the range of g and the range of g is equal to the domain of f.
- If f and g are inverses of each other then their graphs will make reflections of each other on the line y = x.
- If the point (c, d) is on the graph of f then point (d, c) is on the graph of f-1.
Steps to Find the Inverse of One to One Function
The step-by-step procedure to derive the inverse function g-1(x) for a one to one function g(x) is as follows:
- Set g(x) equal to y
- Switch the x with y since every (x, y) has a (y, x) partner
- Solve for y
- In the equation just found, rename y as g-1 (x).
Example: Find the inverse function g-1(x) of the function g(x) = 2 x + 5.
Now, let us follow the 4 steps:

Important Notes on One to One Function:
Here is a list of a few points that should be remembered while studying one to one function:
- In a mathematical sense, one to one functions are functions in which there are equal numbers of items in the domain and in the range, or one can only be paired with another item.
- It is essential for one to understand the concept of one to one functions in order to understand the concept of inverse functions and to solve certain types of equations.
- One can easily determine if a function is one to one geometrically and algebraically too.
Examples on One to One Function
Example 1: Let D = {3, 4, 8, 10} and C = {w, x, y, z}. Which of the following relations represent a one to one function?
{(3, w), (3, x), (3, y), (3, z)}
{(4, w), (3, x), (10, z), (8, y)}
{(4, w), (3, x), (8, x), (10, y)}
For a function to be a one-one function, each element from D must pair up with a unique element from C.
- In the first relation, the same value of x is mapped with each value of y, so it cannot be considered as a function and, hence it is not a one-to-one function.
- In the third relation, 3 and 8 share the same range of x. Hence, it is not a one-to-one function.
- The second relation maps a unique element from D for every unique element from C, thus representing a one-to-one function.
Thus, {(4, w), (3, x), (10, z), (8, y)} represents a one to one function.
Example 2: Determine if g(x) = -3x3 – 1 is a one-to-one function using the algebraic approach.
In order for function to be a one to one function, g( x1 ) = g x2) if and only if x1 = x2. Let us start solving now:
g(x1) = -3 x13–1
g(x2) = -3 x23–1
We will start with g( x1 ) = g(x2). Then
-3 x13 – 1 = -3 x23 – 1
-3 x13 = -3 x23
(x1)3 = (x2)3
Taking the cube root on both sides of the equation will lead us to x1 = x2.
Hence, g(x) = -3x3 – 1 is a one to one function.
Example 3: If the function in Example 2 is one to one, find its inverse. Also, determine whether the inverse function is one to one.
Let g(x) = y. Then y = -3x3 – 1.
Interchange x and y:
x = -3y3 – 1
x + 1 = -3y3
(-x - 1) / 3 = y3
y = ∛[(-x - 1) / 3] = g-1(x)
To determine whether it is one to one, let us assume that g-1( x1 ) = g-1(x2).
∛[(-x1 - 1) / 3] = ∛[(-x2 - 1) / 3]
Cubing on both sides,
(-x1 - 1) / 3 = (-x2 - 1) / 3
Multiplying by 3 on both sides,
-x1 - 1 = -x2 - 1
Adding 1 on both sides,
-x1 = -x2
Multiplying both sides by -1,
x1 = x2
Hence g-1(x) is one to one.
Inverse of g(x) is found and it is proved to be one-one.
|
433 videos|220 docs|166 tests
|





















