Infix, Postfix & Prefix Conversion | Programming and Data Structures - Computer Science Engineering (CSE) PDF Download

Introduction

For writing complex mathematical expressions, we generally prefer parentheses to make them more readable. In computers, expressions with various parentheses add unnecessary work while solving. So, to minimize the computational works, various notations have been made. Prefix and Postfix are one of them.

Definition of Infix, Postfix, and Prefix

Infix: The typical mathematical form of expression that we encounter generally is known as infix notation. In infix form, an operator is written in between two operands.

• For example: An expression in the form of A * ( B + C ) / D is in infix form. This expression can be simply decoded as: “Add B and C, then multiply the result by A, and then divide it by D for the final answer.”

Prefix: In prefix expression, an operator is written before its operands. This notation is also known as “Polish notation”.

• For example: The above expression can be written in the prefix form as / * A + B C D. This type of expression cannot be simply decoded as infix expressions.

Postfix: In postfix expression, an operator is written after its operands. This notation is also known as “Reverse Polish notation”.

• For example, The above expression can be written in the postfix form as A B C + * D /. This type of expression cannot be simply decoded as infix expressions.

Refer to the table below to understand these expressions with some examples:

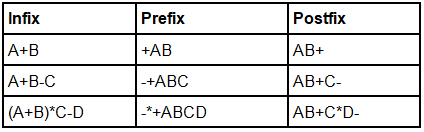
Prefix and postfix notions are methods of writing mathematical expressions without parentheses. Let’s see the infix, postfix and prefix conversion.

Infix to Postfix Conversion

In infix expressions, the operator precedence is implicit unless we use parentheses. Therefore, we must define the operator precedence inside the algorithm for the infix to postfix conversion.
The order of precedence of some common operators is as follows:

Note: For detailed information on the order of precedence, you can check out C Operator Precedence.

Points to consider

• The order of the numbers or operands remains unchanged. But the order of the operators gets changed in the conversion.
• Stacks are used for converting an infix expression to a postfix expression. The stack that we use in the algorithm will change the order of operators from infix to Postfix.
• Postfix expressions do not contain parentheses.

 Algorithm

• Create a stack.
• For each character c in the input stream:

If c is an operand 

{

Output c 

}

Else if c is a right parentheses 

{

Pop and output tokens until a left parentheses is popped  

}

Else

{          // c is an operator or left parentheses

Pop and output tokens until one of the lower priorities than c 

are encountered, or a left parentheses is encountered, or the stack is empty.

Push c

}

• Pop and output tokens until the stack is empty.
  For a better understanding, let’s trace out an example: A * B- (C + D) + E

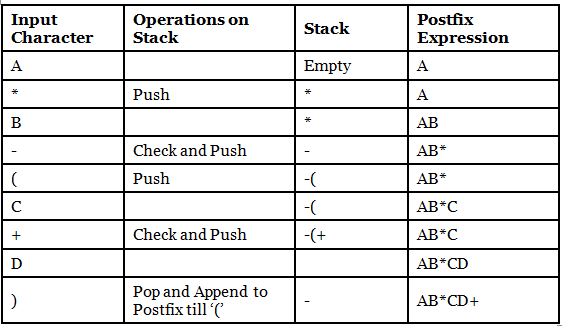
Implementation of the above algorithm

#include<bits/stdc++.h>

using namespace std;

//precedence of operators

int precedence(char ch) 

{

if(ch == '^')

 return 3;

else if(ch == '/' || ch =='*')

 return 2;

else if(ch == '+' || ch == '-')

 return 1;

else

 return -1;

}

string infixToPostfix(string s) 

{

    stack<char> st;

string postfix_exp;

for(int i = 0; i < s.length(); i++) 

    {

 char ch = s[i];

 // If the input character is

 an operand, add it to the postfix output string. if((ch >= 'a' && ch <= 'z') || (ch >= 'A' && ch <= 'Z') || (ch >= '0' && ch <= '9'))

 postfix_exp += ch;

 // If the input character is an

 '(', push it to the stack.

 else if(ch == '(')

 st.push('(');

 // If the input character is an ')',

pop and output string from the stack

 until an '(' is encountered.

 else if(ch == ')') {

 while(st.top() != '(')

 {

  postfix_exp += st.top();

  st.pop();

 }

 st.pop();

 }

 //If the character is an operator

 else 

        {

 while(!st.empty() && precedence(s[i]) <= precedence(st.top())) 

            {

  postfix_exp += st.top();

  st.pop();

 }

 st.push(ch);

 }}

// Pop all the remaining elements from the stack

while(!st.empty()) 

    {

 postfix_exp += st.top();

 st.pop();

}

return postfix_exp;

}

int main() 

{

string infix_expression = "A*B-(C+D)+E";

cout<<"The postfix string is: "<<infixToPostfix(infix_expression);

return 0;

}

Output

The postfix string is: AB*CD+-E+

Prefix to Postfix Conversion 

Converting a prefix expression to a postfix expression is almost the same as the above conversions. The one difference is that we’ll use stack to store operands this time.

Algorithm

• Reverse the prefix string.
• Create a stack.
• For each character c in the input stream:

If c is an operand 

{

Push it in the stack 

}

Else

{          // c is an operator

Pop two tokens(operand) from the stack. Concatenate the operands and the operator, as (operand 1 + operand 2 + operator). And push this string back in the stack 

            }

Note: This string will now act as an operand.

• Repeat until the stack is empty or the input string ends.

For a better understanding, let’s trace out an example: * + A B – C D
Reversed String: D C –  B A + *

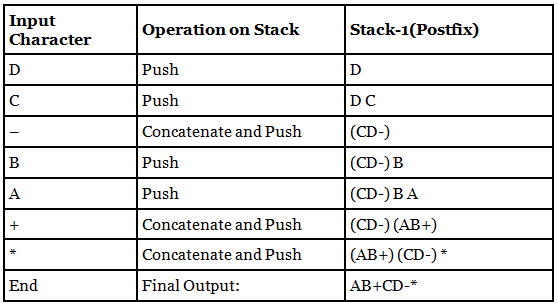
Note: parentheses are only used to represent the string after concatenation.

Implementation of the above algorithm:

#include <bits/stdc++.h>

using namespace std;

// To check if character is operator or not

bool check_op(char x)

{

if(x =='+'|| x== '-'|| x== '/'|| x=='*')

 return true;

else

        return false;

}

// Convert prefix to Postfix expression

string prefixToPostfix(string str)

{

    reverse(str.begin(), str.end());

stack<string> s;

int length = str.size();

    for (int i = 0; i <length; i++)

{

 if (check_op(str[i]))

 {

 string op1 = s.top();

 s.pop();

 string op2 = s.top();

 s.pop();

 string temp = op1 + op2 + str[i];

 s.push(temp);

 }

 else 

        {

 s.push(string(1, str[i]));

 }

}

return s.top();

}

// Driver Code

int main()

{

string str1 = "*+AB-CD";

string str = prefixToPostfix(str1);

cout<<"The postfix string is: "<<str<<endl;

return 0;

}

Output

The postfix string is: AB+CD-*