Arden's Lemma | Theory of Computation - Computer Science Engineering (CSE) PDF Download

Introduction

In order to find out a regular expression of a Finite Automaton, we use Arden’s Theorem along with the properties of regular expressions.

Statement
Let P and Q be two regular expressions.
If P does not contain null string, then R = Q + RP has a unique solution that is R = QP*

Proof
R = Q + (Q + RP)P [After putting the value R = Q + RP]
= Q + QP + RPP
When we put the value of R recursively again and again, we get the following equation:
R = Q + QP + QP2 + QP3…..
R = Q (ε + P + P2 + P3 + …. )
R = QP* [As P* represents (ε + P + P2 + P3 + ….) ]
Hence, proved.

Assumptions for Applying Arden’s Theorem

• The transition diagram must not have NULL transitions
• It must have only one initial state

Method

• Step 1: Create equations as the following form for all the states of the DFA having n states with initial state q₁.
  q₁ = q₁R11 + q2R21 + … + qnRn1 + ε
  q₂ = q₁R1₂ + q2R₂₂ + … + qnRn₂
  …………………………
  …………………………
  …………………………
  …………………………
  q_n = q₁R_1n + q₂R₂n + … + q_nR_nn
  R_ij represents the set of labels of edges from q_i to q_j, if no such edge exists, then R_ij = ∅
• Step 2: Solve these equations to get the equation for the final state in terms of R_ij

Problem 1: Construct a regular expression corresponding to the automata given below

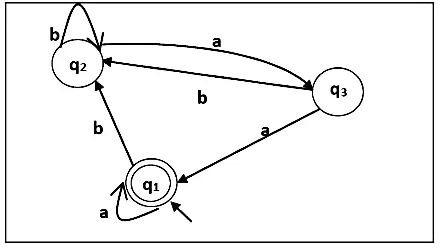
Here the initial state and final state is q₁.
The equations for the three states q₁, q₂, and q₃ are as follows
q₁ = q₁a + q₃a + ε (ε move is because q₁ is the initial state0
q₂ = q₁b + q₂b + q₃b
q₃ = q₂a
Now, we will solve these three equations −
q₂ = q₁b + q₂b + q₃b
= q₁b + q₂b + (q₂a)b (Substituting value of q₃)
= q₁b + q₂(b + ab)
= q₁b (b + ab)* (Applying Arden’s Theorem)
q₁ = q₁a + q₃a + ε
= q₁a + q₂aa + ε (Substituting value of q₃)
= q₁a + q₁b(b + ab*)aa + ε (Substituting value of q₂)
= q₁(a + b(b + ab)*aa) + ε
= ε (a+ b(b + ab)*aa)*
= (a + b(b + ab)*aa)*
Hence, the regular expression is (a + b(b + ab)*aa)*.

Problem 2: Construct a regular expression corresponding to the automata given below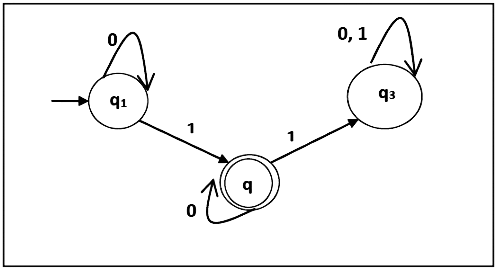

Here the initial state is q₁ and the final state is q₂

Now we write down the equations

q₁ = q₁0 + ε

q₂ = q₁1 + q₂0

q₃ = q₂1 + q₃0 + q₃1

Now, we will solve these three equations

q₁ = ε0* [As, εR = R]

So, q₁ = 0*

q₂ = 0*1 + q₂0

So, q2 = 0*1(0)* [By Arden’s theorem]

Hence, the regular expression is 0*10*.