LCM - Least Common Multiple | Mathematics for Grade 10 PDF Download

The abbreviation LCM stands for 'Least Common Multiple'. The least common multiple (LCM) of two numbers is the lowest possible number that can be divisible by both numbers. It can be calculated for two or more numbers as well.
There are different methods to find the LCM of a given set of numbers. One of the quickest ways to find the LCM of two numbers is to use the prime factorization of each number and then the product of the highest powers of the common prime factors will be the LCM of those numbers.

What is Least Common Multiple (LCM)?

The least common multiple is also known as LCM (or) the lowest common multiple in math. The least common multiple of two or more numbers is the smallest number among all common multiples of the given numbers. Let us take two numbers, 2 and 5. Each will have its own set of multiples.

• Multiples of 2 are 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, …
• Multiples of 5 are 5, 10, 15, 20, …

Now, let us represent these multiples on the number line and circle the common multiples.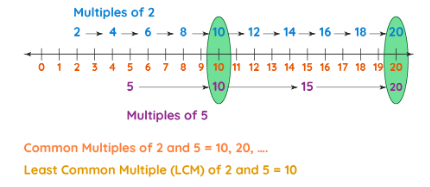

Thus, the common multiples of 2 and 5 are 10, 20, ….. The smallest number among 10, 20, … is 10.
So the least common multiple of 2 and 5 is 10.
It can be written as LCM (2, 5) = 10.

How to Find LCM?

LCM of numbers can be calculated using various methods. There are 3 methods to find the least common multiple of two numbers. Each method is explained below with some examples.

• LCM by Listing Method
• LCM by Prime Factorization Method
• LCM using Division Method

LCM by Listing Method

We can find out the common multiples of two or more numbers by listing their multiples. Out of these common multiples, the least common multiple is considered and the LCM of two given numbers can thus be calculated. To calculate the LCM of the two numbers A and B by the listing method, we use the steps given below:

• Step 1: List the first few multiples of A and B.
• Step 2: Mark the common multiples from the multiples of both numbers.
• Step 3: Select the smallest common multiple. That lowest common multiple is the LCM of the two numbers.

Example: Find the least common multiple (LCM) of 4 and 5.
Solution: The first few multiples of 4 are: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, ...
And the first few multiples of 5 are: 5, 10, 15, 20, 25, 30, 35, 40, ...

We can observe that 20 is the least multiple which is common in the multiples of 4 and 5. Therefore, the least common multiple (LCM of 4 and 5) is 20.

LCM by Prime Factorization Method

By using the prime factorization method we can find out the LCM of the given numbers. To calculate the LCM of two numbers using the prime factorization method, we use the steps given below:

• Step 1: Find the prime factors of the given numbers by repeated division method.
• Step 2: Write the numbers in their exponent form. Find the product of only those prime factors that have the highest power.
• Step 3: The product of these factors with the highest powers is the LCM of the given numbers.

This method using the example given below.
Example: Find the least common multiple (LCM) of 60 and 90 using prime factorization.
Solution: Let us find the LCM of 60 and 90 using the prime factorization method.

• Step 1: The prime factorization of 60 and 90 are: 60 = 2 × 2 × 3 × 5 and 90 = 2 × 3 × 3 × 5
• Step 2: If we write these prime factors in their exponent form it will be expressed as, 60 = 22 × 31 × 51 and 90 = 21 × 32 × 51
• Step 3: Now, we will find the product of only those factors that have the highest powers among these. This will be, 22 × 32 × 51 = 4 × 9 × 5 = 180

Therefore, LCM of 60 and 90 = 180.

LCM by Division Method

In order to find the LCM by division method, we divide the numbers by a common prime number, and these prime factors are used to calculate the LCM of those numbers. Let us understand this method using the steps given below:

• Step 1: Find a prime number which is a factor of at least one of the given numbers. Write this prime number on the left of the given numbers.
• Step 2: If the prime number in step 1 is a factor of the number, then divide the number by the prime and write the quotient below it. If the prime number in step 1 is not a factor of the number, then write the number in the row below as it is. Continue the steps until 1 is left in the last row.

This method using the example given below.
Example: Find the least common multiple (LCM) of 6 and 15 using the division method.
Solution: Let us find the least common multiple (LCM) of 6 and 15 using the division method using the steps given below.

• Step 1: 2 is the smallest prime number and it is a factor of 6. Write 2 on the left of the two numbers. For each number in the right column, continue finding out prime numbers which are their factors.
• Step 2: 2 divides 6 but it is not a factor of 15, so we write the number 15 in the row below as it is. Continue the steps until 1 is left in the last row. Then, we divide 3 and 15 by 3. This gives us 1 and 3. Now, again we write 5 on the left side and we finally get 1, 1 as the quotient in the last row.
• Step 3: Then we multiply these numbers on the left. The LCM is the product of all these prime numbers. LCM of 6 and 15 is, 2 × 3 × 5 = 30.

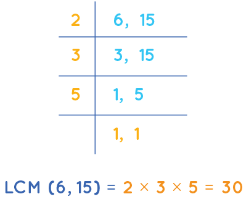
Though we have three methods to find the least common multiple, the division method is the most common and easy method that we use. Use the online LCM calculator to verify your answers.

LCM Formulas

LCM formulas are the collection of the numbers, their LCM, and their HCF (Highest Common Factor). These formulas are used to calculate the least common multiple of two integers as well as the LCM of two fractions. The LCM formulas for integers and fractions are shown below.

LCM Formula for Integers

If a and b are the two integers then the formula for their least common multiple is given as:
LCM (a, b) = (a × b)/HCF(a, b)

Relationship Between LCM and HCF

The Highest Common Factor (HCF) of a given set of numbers is the highest factor which is common among the factors of the given numbers. It is calculated by multiplying the common prime factors of the given numbers. Whereas the least common multiple (LCM) of two or more numbers is the smallest number among all common multiples of the given numbers. Let us assume a and b are the two numbers, then the formula that expresses the relationship between their LCM and HCF is given as:
LCM (a,b) × HCF (a,b) = a × b
or, Product of the two numbers = LCM of the numbers × HCF of the numbers

Difference Between LCM and HCF

The HCF or the highest common factor of two or more numbers is the highest or the greatest factor among all the common factors of the given numbers, whereas the LCM or the least common multiple of two or more numbers is the smallest number among all common multiples of the given numbers. The following table shows the difference between HCF and LCM: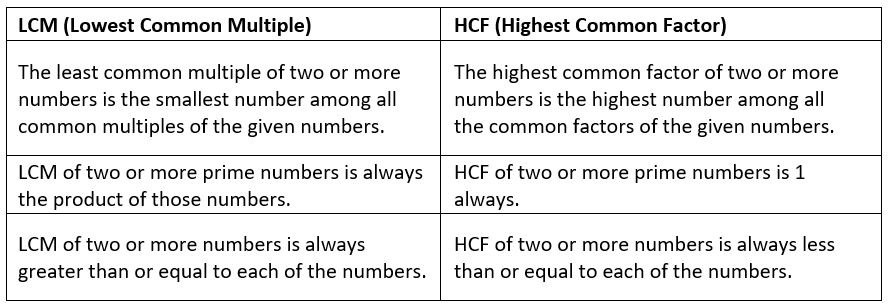

LCM of Three Numbers

The LCM of 3 numbers can be calculated using the same methods given above. Let us understand how to find the LCM of 25, 15, and 30 using the prime factorization method.
Example: Find the LCM of 25, 15, and 30 using the prime factorization method.

Solution: Let us use the following steps to find the LCM of the 3 numbers.

• Step 1: Find the prime factors of the given numbers by repeated division method. Here, it will be as follows: prime factorization of 25 = 5 × 5; prime factorization of 15 = 3 × 5; prime factorization of 30 = 2 × 3 × 5
• Step 2: If we write these prime factors in their exponents form it will be expressed as, 25 = 5², 15 = 3¹ × 5¹, and 30 = 2¹ × 3¹ × 5¹
• Step 3: Now, we will find the product of only those factors with the highest powers. It should be noted that we take one factor only once. This will be, 5² × 3¹ × 2¹ = 150

Now let us find the LCM of these 3 numbers by the listing method.
Example: Find the LCM of 25, 15, and 30 by listing method.
Solution: Let us use the following steps to find the LCM of the 3 numbers.

• Step 1: List the first few multiples of all the three numbers, This will be:
• Multiples of 25 = 25, 50, 75, 100, 125, 150, 175, ....,
• Multiples of 15 = 15, 30, 45, 60, 75, 90, 105, 120, 135, 150, 175, ....
• Multiples of 30 = 30, 60, 90, 120, 150, 180, 210, ...
• Step 2: Among the common multiples of 25, 15 and 30 we can see that 150 is the least multiple that is common in all three numbers. Therefore, the LCM of 25, 15 and 30 = 150.