Adding and Subtracting Polynomials | The Complete SAT Course - Class 10 PDF Download
While addition and subtraction of polynomials, we simply add or subtract the terms of the same power. The power of variables in a polynomial is always a whole number, power can not be negative, irrational, or a fraction. It is straightforward to add or subtract two polynomials. A polynomial is a mathematics expression written in the form of a0Xn + a1xn−1 + a2xn−2 + ...... + anX0.
The above expression is also called polynomial in standard form, where a0, a1, a2 ......... an are constants, and n is a whole number. For example x2 + 2x + 3, 5x4 - 4x2 + 3x + 1 and 7x - √3 are polynomials.
How Can We Add Polynomials?
The addition of polynomials is simple. While adding polynomials, we simply add like terms. We can use columns to match the correct terms together in a complicated sum. Keep two rules in mind while performing the addition of polynomials.
- Rule 1: Always take like terms together while performing addition.
- Rule 2: Signs of all the polynomials remain the same.
- For example, Add 2x2 + 3x +2 and 3x2 - 5x -1
- Step 1: Arranging the polynomial in standard form. In this case, they are already in their standard forms.
- Step 2: Like terms in the above two polynomials are:
- 2x2 and 3x2; 3x and -5x; 2 and -1.
- Step 3: Calculations with signs remaining same:
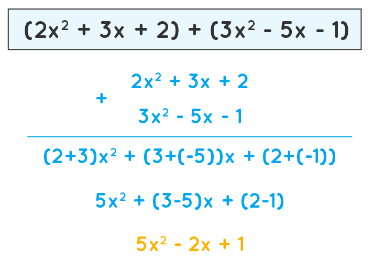
- Like Terms
Like Terms are terms whose variables, along with their exponents, are the same. For example, 2x, 7x, -2x, etc are all like variables. - Unlike Terms
Unlike Terms are terms whose either variables, exponents, or both variables and exponents are the not same. For example, 2, 7x2, -2y2, etc are all unlike variables.
Subtraction of Polynomials
The subtraction of polynomials is as simple as the addition of polynomials. Using columns would help us to match the correct terms together in a complicated subtraction. While subtracting polynomials, separate the like terms and simply subtract them. Keep two rules in mind while performing the subtraction of polynomials.
- Rule 1: Always take like terms together while performing subtraction.
- Rule 2: Signs of all the terms of the subtracting polynomial will change, + changes to - and - changes to +.
- For example, we have to subtract 2x2 + 3x +2 from 3x2- 5x -1
- Step 1: Arranging the polynomial in standard form. In this case, they are already in their standard forms.
- Step 2: Like terms in the above two polynomials are: 2x2 and 3x2; 3x and -5x; 2 and -1
- Step 3: Enclose the part of the polynomial which to be deducted in parentheses with a negative (-) sign prefixed. Then, remove the parentheses by changing the sign of each term of the polynomial expression.
- Step 4: Calculations after altering the signs of the subtracting polynomials:
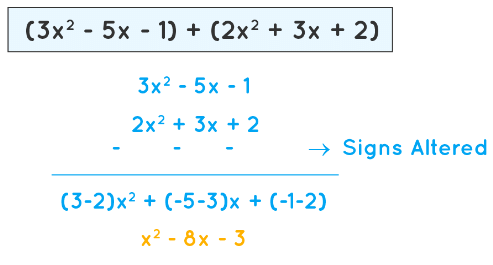
Steps for Adding and Subtracting Polynomials
The addition or subtraction of polynomials is very simple to perform, all we need to do is to keep some steps in mind. To perform the addition and subtraction operation on the polynomials, the polynomials can be arranged vertically for complex expressions. For simpler calculations, we can perform the operation using the horizontal arrangement.
Adding and Subtracting Polynomials Horizontally
Polynomials can be added and subtracted in horizontal arrangement using the steps given below,
- Step 1: Arrange the polynomials in their standard form.
- Step 2: Place the polynomial next to each other horizontally.
- Step 3: First separate the like terms.
- Step 4: Arrange the like terms together.
- Step 5: Signs of all the polynomials remain the same in addition. While in Subtraction, the signs of the terms in subtracting polynomial change.
- Step 6: Perform the calculations.
Adding and Subtracting Polynomials Vertically
Polynomials can be added and subtracted in vertical arrangement using the steps given below,
- Step 1: Arrange the polynomials in their standard form
- Step 2: Place the polynomials in a vertical arrangement, with the like terms placed one above the other in both the polynomials.
- Step 3: We can represent the missing power term in the standard form with "0" as the coefficient to avoid confusion while arranging terms.
- Step 4: Signs of all the polynomials remain the same in addition. While in Subtraction, the signs of the terms in subtracting polynomial change.
- Step 5: Perform the calculations
By following these steps we can solve adding and subtracting polynomials.
Example: (3x3 + x2 - 2x -1) + (x3 + 6x + 3).
The given polynomials are arranged in their standard forms.
Addition performed horizontally:
- Step 1: Separate the like terms: 3x3 and x3; x2; -2x and 6x; -1 and 3
- Step 2: Arrange the like terms together: 3x3 + x3 + x2 + (-2x + 6x) + (-1 + 3)
- Step 3: Perform the calculations: (3 + 1)x3 + x2 + (-2 + 6)x + (-1 + 3)= 4x3 + x2 + 4x + 2
Addition performed vertically:
- Step 1: Arrange both the polynomials one above the other with like terms place one above the other. We can represent the missing power term in the standard form with "0" as the coefficient to avoid confusion while arranging terms.
- Step 2: Perform the calculations.
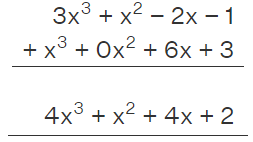
Important Notes
- The highest power of the variable in a polynomial is called the degree of the polynomial.
- The algebraic expressions having negative or irrational power of the variable are not polynomials.
- Addition and subtraction in polynomials can only be performable on like terms.
Example: Add two polynomials, 3x + 2y, and 4y + 5z to find the solution.
Solution: Given polynomials are (3x + 2y) + (4y + 5z). Here like terms are only 2y and 4y.
So addition can only be performed on these two terms, the other terms 3x and 5z will not get affected.
3x + (2y + 4y) + 5z
= 3x + (2 + 4)y + 5z
= 3x + 6y + 5z
Therefore, answer is 3x + 6y + 5z.
|
433 videos|220 docs|166 tests
|
















