Long Division of Polynomials | Mathematics for ACT PDF Download

Long division of polynomials is the process of dividing one polynomial with another. Division can be done among the different types of polynomials i.e. between two monomials, a polynomial and a monomial, or between two polynomials. A polynomial is n algebraic expression with variables, terms, and coefficients with the degree of the expressions. Let us explore the division of polynomials by learning about the methods to divide using long division, long division with polynomials, long division with missing terms, the algorithm, and solved a few examples to understand the process better.

What is Long Division of Polynomials?

A long division polynomial is an algorithm for dividing polynomial by another polynomial of the same or a lower degree. The long division of polynomials also consists of the divisor, quotient, dividend, and the remainder as in the long division method of numbers. Observe the numerator and denominator in the long division of polynomials as shown in the figure.

The long division of polynomials also consists of a divisor, a quotient, a dividend, and a remainder.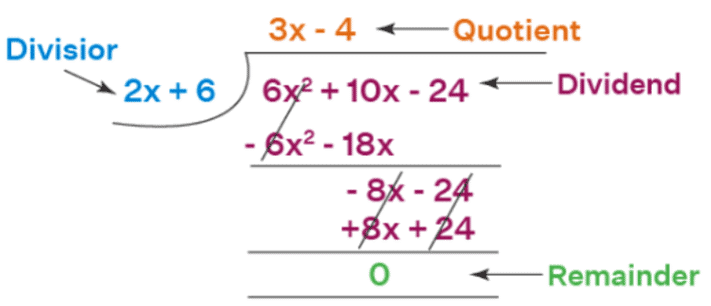

In algebra, the division of algebraic expressions can be done in three ways: 

• Division of a monomial by another monomial.
• Division of a polynomial by a monomial.
• Division of a polynomial by a binomial.
• Division of a polynomial by another polynomial.

Steps For Long Division of Polynomials

The following are the steps for the long division of polynomials:

• Step 1. Arrange the terms in the decreasing order of their indices (if required). Write the missing terms with zero as their coefficient.
• Step 2. For the first term of the quotient, divide the first term of the dividend by the first term of the divisor.
• Step 3. Multiply this term of the quotient by the divisor to get the product.
• Step 4. Subtract this product from the dividend, and bring down the next term (if any). The difference and the brought down term will form the new dividend.
• Step 5. Follow this process until you get a remainder, which can be zero or of a lower index than the divisor.

Long Division of Polynomial by Missing Terms

While performing long division of polynomials, there can be a missing term in the expression, for example, 6x⁴ + 3x - 9x² + 6, x³ is missing. In this case, we either leave a gap while dividing or we write the coefficient as zero. Let's understand how to do the long division of polynomials with the same example. We need to divide the polynomial a(x) = 6x⁴ + 3x - 9x² + 6 by the quadratic polynomial b(x) = x² - 2
Arrange the polynomial in the descending order of the power of the variable.
a(x) = 6x⁴ - 9x² + 3x + 6
b(x) = x² - 2
Divide a(x) by b(x) in the same way as we divide numbers.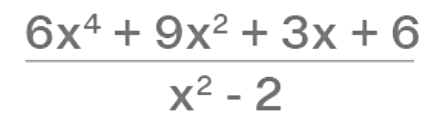

Add the missing indices with zero (0) as the coefficient.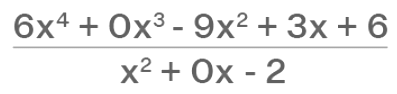

Divide 6x⁴ by x² to get the first term of the quotient. We get 6x².

Multiply the divisor by 6x².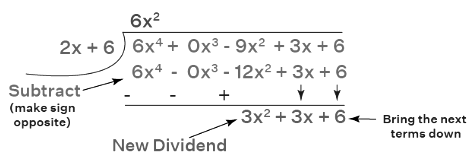

Divide 3x² by x² to get the next term of the quotient.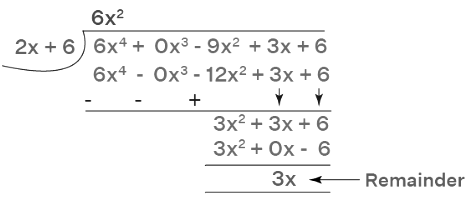

As the power of the next dividend is less than the divisor, we get our required remainder. Please remember that as the remainder we got is a non-zero term, we can say that x² - 2 is not a factor of 6x⁴ - 9x² + 3x + 6. Therefore, the quotient is 6x² + 3 and the remainder is 3x.

Long Division of Polynomials by Monomials

While dividing polynomials by monomials, write the common factor between the numerator and the denominator of the polynomial and divide each term separately. Once the result is obtained, add all the terms together to form an expression. For example: Divide the following polynomial: (2x² + 4x + 8xy) ÷ 2x. Both the numerator and denominator have a common factor of 2x. Thus, the expression can be written as 2x(x + 2 + 4y) / 2x. Canceling out the common term 2x, we get x + 4y + 2 as the answer.

Long Division of Polynomials by Other Monomial

Long division of polynomials by another monomial is done in a similar manner as done for polynomials by monomials. The factors of the monomial of both the numerator and denominator are listed out and the long division takes place. For example, divide 62x³ by 2x. The factors of 62x³ = 2 × 31 × x × x × x and 2x = 2 × x. The common factors for both are 2x. Hence, 62x³/2x = 31x².

Long Division of Polynomials by Binomials

Long division of polynomials by binomials is done when there are no common factors between the numerator and the denominator, or if you can't find the factors. Let us go through the algorithm of dividing polynomials by binomials using an example: Divide: (6x² - 4x - 24) ÷ (x - 3). Here, (6x² - 4x - 24) is the dividend, and (x - 3) is the divisor which is a binomial. Observe the division shown below, followed by the steps.

• Step 1. Divide the first term of the dividend (6x²) by the first term of the divisor (x), and put that as the first term in the quotient (6x).
• Step 2. Multiply the divisor by that answer, place the product (6x² - 18x) below the dividend.
• Step 3. Subtract to create a new polynomial (14x - 24).
• Step 4. Repeat the same process with the new polynomial obtained after subtraction.

So, when we are dividing a polynomial (6x² - 4x - 24) with a binomial (x - 3), the quotient is 6x + 14 and the remainder is 18.

Long Division of Polynomials by Other Polynomial

Long division of a polynomial with another polynomial is done when the expression is written in the standard form i.e. the terms of the dividend and the divisor are arranged in decreasing order of their degrees. The long division method for polynomials is considered the generalized version of the simple long division method done with numbers. Let us look at an example to understand this better. The process of division is very similar to the rest of the methods. Divide the polynomial 6x³ + 12x² + 2x + 25 by x² + 4x + 3. Here, 6x³ + 12x² + 2x + 25 is the dividend, and x² + 4x + 3 is the divisor which is also a polynomial.

• Step 1: Divide the first term of the dividend (6x³) by the first term of the divisor (x²), and put that as the first term in the quotient (6x).
• Step 2: Multiply the divisor by that answer, place the product (6x³ + 24x² + 18x) below the dividend.
• Step 3: Subtract to create a new polynomial (-12x² - 16x + 25).
• Step 4: Repeat the same process with the new polynomial obtained after subtraction.

So, when we are dividing a polynomial 6x³ + 12x² + 2x + 25 with a binomial x² + 4x + 3, the quotient is 6x - 12 and the remainder is 32x + 61.

Long Division Algorithm of Polynomials

The division algorithm for polynomials says, if p(x) and g(x) are the two polynomials, where g(x) ≠ 0, we can write the division of polynomials as: p(x) = q(x) × g(x) + r(x).

Where,

• p(x) is the dividend.
• q(x) is the quotient.
• g(x) is the divisor.
• r(x) is the remainder.
• r(x) = 0 or degree of r(x) < degree of g(x)

If we compare this to the regular division of numbers, we can easily understand this as: Dividend = (Divisor X Quotient) + Remainder. Let us take the previous example,
p(x) = 6x³ + 12x² + 2x + 25
g(x) = x² + 4x + 3
q(x) = 6x - 12
r(x) = 32x + 61
Apply the division algorithm, q(x) × g(x) + r(x)
(6x - 12) × (x² + 4x + 3) + (32x + 61)
6x³ + 24x² + 18x - 12x² - 48x - 36 + 32x + 61
6x³ + 12x² - 2x + 25
= p(x).
Hence, the division algorithm is verified.