How to Divide Polynomials? | Mathematics for ACT PDF Download

Dividing polynomials is an arithmetic operation where we divide a polynomial by another polynomial, generally with a lesser degree as compared to the dividend. The division of two polynomials may or may not result in a polynomial.

What is Dividing Polynomials?

Polynomials are algebraic expressions that consist of variables and coefficients. It is written in the following format: 5x² + 6x - 17. This polynomial has three terms that are arranged according to their degree. The term with the highest degree is placed first, followed by the lower ones. Dividing polynomials is an algorithm to solve a rational number that represents a polynomial divided by a monomial or another polynomial. The divisor and the dividend are placed exactly the same way as we do for regular division. For example, if we need to divide 5x² + 7x + 25 by 6x - 25, we write it in this way: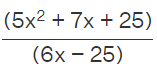

The polynomial written on top of the bar is the numerator (5x² + 7x + 25), while the polynomial written below the bar is the denominator (6x - 25). This can be understood by the following figure which shows that the numerator becomes the dividend and the denominator becomes the divisor.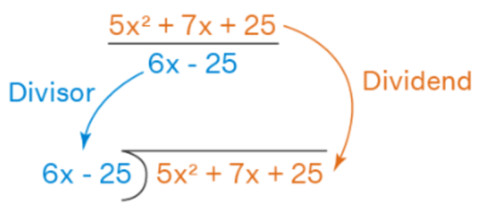

Dividing Polynomials by Monomials

While dividing polynomials by monomials, the division can be done in two ways. One is by simply separating the '+' and '-' operator signs. That means, we break the polynomial from the operating sign, and solve each part separately. Another method is to do the simple factorization and further simplifying. Let us have a look at both methods in detail.

Splitting the Terms Method

Split the terms of the polynomial separated by the operator ( '+' or '-' ) between them and simplify each term. For example, (4x² - 6x) ÷ (2x) can be solved as shown here. We first take common terms from the numerators and denominators of both the terms, we get, [(4x²) / (2x)] - [(6x) / (2x)]. Canceling the common term 2x from the numerator and the denominator, we get 2x - 3.

Factorization Method

When you divide polynomials you may have to factor the polynomial to find a common factor between the numerator and the denominator. For example: Divide the following polynomial: (2x² + 4x) ÷ 2x. Both the numerator and denominator have a common factor of 2x. Thus, the expression can be written as 2x(x + 2) / 2x. Canceling out the common term 2x, we get x+2 as the answer.

Dividing Polynomials by Binomials

For dividing polynomials by binomials or any other type of polynomials, the most common and general method is the long division method. When there are no common factors between the numerator and the denominator, or if you can't find the factors, you can use the long division process to simplify the expression.

Dividing Polynomials Using Long Division
Let us go through the algorithm of dividing polynomials by binomials using an example: Divide: (4x² - 5x - 21) ÷ (x - 3). Here, (4x² - 5x - 21) is the dividend, and (x - 3) is the divisor which is a binomial. Observe the division shown below, followed by the steps.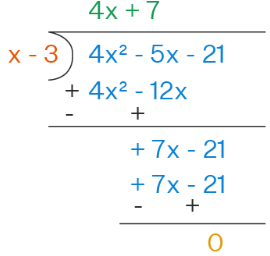

• Step 1. Divide the first term of the dividend (4x²) by the first term of the divisor (x), and put that as the first term in the quotient (4x).
• Step 2. Multiply the divisor by that answer, place the product (4x² - 12x) below the dividend.
• Step 3. Subtract to create a new polynomial (7x - 21).
• Step 4. Repeat the same process with the new polynomial obtained after subtraction.

So, when we are dividing a polynomial (4x² - 5x - 21) with a binomial (x - 3), the quotient is 4x+7 and the remainder is 0.

Dividing Polynomials Using Synthetic Division

Synthetic division is a technique to divide a polynomial with a linear binomial by only considering the values of the coefficients. In this method, we first write the polynomials in the standard form from the highest degree term to the lowest degree terms. While writing in descending powers, use 0's as the coefficients of the missing terms. For example, x3+3 has to be written as x³ + 0x² + 0x + 3. Follow the steps given below for dividing polynomials using the synthetic division method:
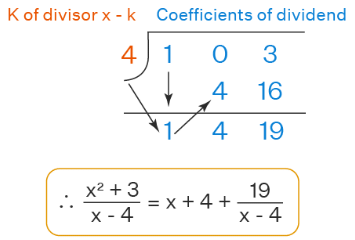
Let us divide x² + 3 by x - 4.

• Step 1: Write the divisor in the form of x - k and write k on the left side of the division. Here, the divisor is x-4, so the value of k is 4.
• Step 2: Set up the division by writing the coefficients of the dividend on the right and k on the left. [Note: Use 0's for the missing terms in the dividend]
• Step 3: Now, bring down the coefficient of the highest degree term of the dividend as it is. Here, the leading coefficient is 1 (coefficient of x²).
• Step 4: Multiply k with that leading coefficient and write the product below the second coefficient from the left side of the dividend. So, we get, 4×1=4 that we will write below 0.
• Step 5: Add the numbers written in the second column. Here, by adding we get 0+4=4.
• Step 6: Repeat the same process of multiplication of k with the number obtained in step 5 and write the product in the next column to the right.
• Step 7: At last, we will write the final answer which will be one degree less than the dividend. So, here, in our dividend, the highest degree term is x², therefore, in the quotient, the highest degree term will be x. Therefore, the answer obtained is x+4+(19/x-4).