Trigonometric Ratios | Mathematics for ACT PDF Download

Introduction

Trigonometric ratios are the ratios of the length of sides of a triangle. These ratios in trigonometry relate the ratio of sides of a right triangle to the respective angle. The basic trigonometric ratios are sin, cos, and tan, namely sine, cosine, and tangent ratios. The other important trig ratios, cosec, sec, and cot, can be derived using the sin, cos, and tan respectively.
The word "Trigonometry" originated from the words, "Trigonon" which means "triangle" and "Metron" which means "to measure". It is a branch of mathematics that deals with the relation between the angles and sides of a right-angled triangle. In fact, trigonometry is one of the most ancient subjects which is studied by scholars all over the world.

What are Trigonometric Ratios?

In trigonometry, there are six trigonometric ratios, namely, sine, cosine, tangent, secant, cosecant, and cotangent. These ratios are written as sin, cos, tan, sec, cosec(or csc), and cot in short. Let us have a look at the right-angled triangle shown below. Trigonometric ratios can be used to determine the ratios of any two sides out of a total of three sides of a right-angled triangle in terms of the respective angles.
The values of these trigonometric ratios can be calculated using the measure of an acute angle, θ in the right-angled triangle given below. This implies that the value of the ratio of any two sides of the triangle here depends on angle C. We can alternatively find the values of these trig ratios for angle A. Also, only the base and perpendicular will interchange for the given right triangle in that case.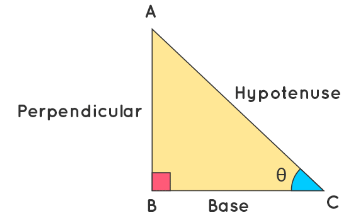

These six trigonometric ratios can be defined as, 
Sine: The sine ratio for any given angle is defined as the ratio of the perpendicular to the hypotenuse. In the given triangle, sine of angle θ can be given as, sin θ = AB/AC.
Cosine: The cosine ratio for any given angle is defined as the ratio of the base to the hypotenuse. In the given triangle, cosine of angle θ can be given as, cos θ = BC/AC.
Tangent: The tangent ratio for any given angle is defined as the ratio of the perpendicular to the base. In the given triangle, the tangent of angle θ can be given as, tan θ = AB/BC.
Cosecant: The cosecant ratio for any given angle is defined as the ratio of the hypotenuse to the perpendicular. In the given triangle, cosecant of angle θ can be given as, cosec θ = AC/AB.
Secant: The secant ratio for any given angle is defined as the ratio of the hypotenuse to the base. In the given triangle, secant of angle θ can be given as, sec θ = AC/BC.
Cotangent: The cotangent ratio for any given angle is defined as the ratio of the base to the perpendicular. In the given triangle, cotangent of angle θ can be given as, cot θ = BC/AB.
Let us understand these and more trigonometric ratio formulas in detail in the next section.

Trigonometric Ratios Formulas

Trigonometric ratios can be calculated by taking the ratio of any two sides of the right-angled triangle. We can evaluate the third side using the Pythagoras theorem, given the measure of the other two sides. We can use the abbreviated form of trigonometric ratios to compare the length of any two sides with the angle in the base. The angle θ is an acute angle (θ < 90º) and in general is measured with reference to the positive x-axis, in the anticlockwise direction. The basic trigonometric ratios formulas are given below,

• sin θ = Perpendicular/Hypotenuse
• cos θ = Base/Hypotenuse
• tan θ = Perpendicular/Base
• sec θ = Hypotenuse/Base
• cosec θ = Hypotenuse/Perpendicular
• cot θ = Base/Perpendicular

Now, let us observe the reciprocal trigonometric ratio formulas of the above-mentioned trigonometric ratios. As we observe, we notice that sin θ is a reciprocal of cosec θ, cos θ is a reciprocal of sec θ, tan θ is a reciprocal of cot θ, and vice-versa. So, the new set of formulas for trigonometric ratios is:

• sin θ = 1/cosec θ
• cos θ = 1/sec θ
• tan θ = 1/cot θ
• cosec θ = 1/sin θ
• sec θ = 1/cos θ
• cot θ = 1/tan θ

Trigonometric Ratios Table

In the trigonometric ratios table, we use the values of trigonometric ratios for standard angles 0°, 30°, 45°, 60°, and 90º. It is easy to predict the values of the table and to use the table as a reference to calculate values of trigonometric ratios for various other angles, using the trigonometric ratio formulas for existing patterns within trigonometric ratios and even between angles. Now, we will summarize the value of trigonometric ratios for specific angles in the table below: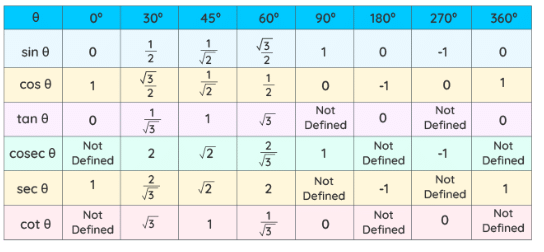

Trigonometric Ratios Identities

There are many trigonometric ratios identities that we use to make our calculations easier and simpler. These include identities of complementary angles, supplementary angles, Pythagorean identities, and sum, difference, product identities.

Trigonometric Ratios of Complementary Angles Identities

The complementary angles are a pair of two angles such that their sum is equal to 90°. The complement of an angle θ is (90° - θ). The trigonometric ratios of complementary angles are:

• sin (90°- θ) = cos θ
• cos (90°- θ) = sin θ
• cosec (90°- θ) = sec θ
• sec (90°- θ) = cosec θ
• tan (90°- θ) = cot θ
• cot (90°- θ) = tan θ

Pythagorean Triogometric Ratios Identities

The Pythagorean trigonometric ratios identities in trigonometry are derived from the Pythagoras theorem. Applying Pythagoras theorem to the right-angled triangle below, we get:
Opposite² + Adjacent² = Hypotenuse²
Dividing both sides by Hypotenuse²
Opposite²/Hypotenuse² + Adjacent²/Hypotenuse² = Hypotenuse²/Hypotenuse²

• sin²θ + cos²θ = 1

This is one of the important Pythagorean identities. In the same way, we can derive two other Pythagorean trigonometric ratios identities:

• sin²θ + cos²θ = 1
• 1 + tan²θ = sec²θ
• 1 + cot²θ = cosec²θ

Sum, Difference, Product Trigonometric Ratios Identities

The sum, difference, and product trigonometric ratios identities include the formulas of sin(A+B), sin(A-B), cos(A+B), cos(A-B), etc.

• sin (A + B) = sin A cos B + cos A sin B
• sin (A - B) = sin A cos B - cos A sin B
• cos (A + B) = cos A cos B - sin A sin B
• cos (A - B) = cos A cos B + sin A sin B
• tan (A + B) = (tan A + tan B)/ (1 - tan A tan B)
• tan (A - B) = (tan A - tan B)/ (1 + tan A tan B)
• cot (A + B) = (cot A cot B - 1)/(cot B - cot A)
• cot (A - B) = (cot A cot B + 1)/(cot B - cot A)
• 2 sin A⋅cos B = sin(A + B) + sin(A - B)
• 2 cos A⋅cos B = cos(A + B) + cos(A - B)
• 2 sin A⋅sin B = cos(A - B) - cos(A + B)

Half, Double, and Triple-Angles Trigonometric Ratios Identities

Double Angle Trigonometric Ratios Identities
The double angle trigonometric identities can be obtained by using the sum and difference formulas.
For example, from the above formula sin (A+B) = sin A cos B + cos A sin B
Substitute A = B = θ on both sides here, we get:
sin (θ + θ) = sinθ cosθ + cosθ sinθ
sin 2θ = 2 sinθ cosθ

In the same way, we can derive the other double angle identities.

• sin 2θ = 2 sinθ cosθ
• cos 2θ = cos²θ - sin²θ
  cos 2θ = 2 cos²θ - 1
  cos 2θ = 1 - 2 sin²θ
  cos 2θ = (1 - tan² θ)/(1 + tan²θ)
• tan 2θ = (2 tanθ)/ (1 - tan²θ)
• sec 2θ = sec²θ/(2-sec²θ)
• cosec 2θ = (sec θ. cosec θ)/2
• cot 2θ = (cot θ - tan θ)/2

Half Angle Trigonometric Ratios Identities
Using one of the above double angle formulas,
cos 2θ = 1 - 2 sin²θ
2 sin²θ = 1- cos 2θ
sin²θ = (1 - cos 2θ)/(2)
sin θ = ±√[(1 - cos 2θ)/2]
Replacing θ by θ/2 on both sides,
sin (θ/2) = ±√[(1 - cos θ)/2]
This is the half-angle formula of sine.

In the same way, we can derive the other half-angle formulas.

• sin (θ/2) =±√[(1 - cos θ)/2]
• cos (θ/2) = ±√[(1 + cos θ)/2]
• tan (θ/2) = ±√[(1 - cos θ)(1 + cosθ)]

Triple Angle Trigonometric Ratios Identities

• sin 3θ = 3sin θ - 4sin³θ
• cos 3θ = 4cos³θ - 3cos θ
• tan 3θ = (3tanθ - tan³θ)/(1 - 3tan²θ)

Example on Trigonometric Ratios

Example: In a right-angled triangle ABC, right-angled at B, hypotenuse AC = 10 units, base BC = 8 units and perpendicular AB = 6 units and if ∠ACB = θ, then find the trigonometric ratios tan θ, sin θ, and cos θ.

We know,
sin θ = perpendicular/hypotenuse
cos θ = base/hypotenuse
tan θ = perpendicular/base
⇒ sin θ = 6/10 = 3/5
⇒ cos θ = 8/10 = 4/5
⇒ tan θ = 6/8 = 3/4