Equations of a Unit Circle | The Complete SAT Course - Class 10 PDF Download
A unit circle from the name itself defines a circle of unit radius. A circle is a closed geometric figure without any sides or angles. The unit circle has all the properties of a circle, and its equation is also derived from the equation of a circle. Further, a unit circle is useful to derive the standard angle values of all the trigonometric ratios.
Here we shall learn the equation of the unit circle, and understand how to represent each of the points on the circumference of the unit circle, with the help of trigonometric ratios of cosθ and sinθ.
What is Unit Circle?
A unit circle is a circle with a radius measuring 1 unit. The unit circle is generally represented in the cartesian coordinate plane. The unit circle is algebraically represented using the second-degree equation with two variables x and y. The unit circle has applications in trigonometry and is helpful to find the values of the trigonometric ratios sine, cosine, tangent.
Unit Circle Definition
The locus of a point which is at a distance of one unit from a fixed point is called a unit circle.
Equation of a Unit Circle
The general equation of a circle is (x - a)2 + (y - b)2 = r2, which represents a circle having the center (a, b) and the radius r. This equation of a circle is simplified to represent the equation of a unit circle. A unit circle is formed with its center at the point(0, 0), which is the origin of the coordinate axes. and a radius of 1 unit. Hence the equation of the unit circle is (x - 0)2 + (y - 0)2 = 12. This is simplified to obtain the equation of a unit circle.
Equation of a Unit Circle: x2 + y2 = 1
Here for the unit circle, the center lies at (0, 0) and the radius is 1 unit. The above equation satisfies all the points lying on the circle across the four quadrants.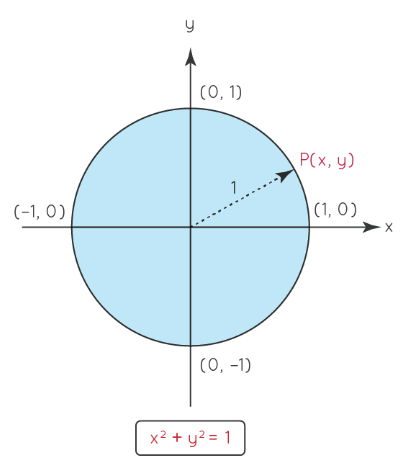
Finding Trigonometric Functions Using a Unit Circle
We can calculate the trigonometric functions of sine, cosine, and tangent using a unit circle. Let us apply the Pythagoras theorem in a unit circle to understand the trigonometric functions. Consider a right triangle placed in a unit circle in the cartesian coordinate plane. The radius of the circle represents the hypotenuse of the right triangle. The radius vector makes an angle θ with the positive x-axis and the coordinates of the endpoint of the radius vector is (x, y). Here the values of x and y are the lengths of the base and the altitude of the right triangle. Now we have a right angle triangle with the sides 1, x, y. Applying this in trigonometry, we can find the values of the trigonometric ratio, as follows:
- sinθ = Altitude/Hypoteuse = y/1
- cosθ = Base/Hypotenuse = x/1
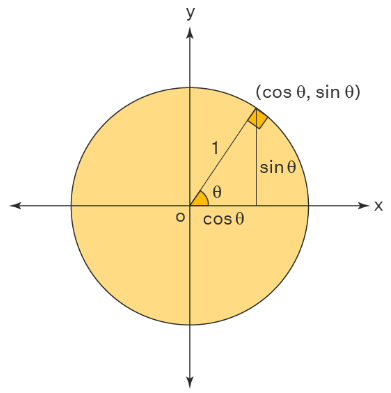
We now have sinθ = y, cosθ = x, and using this we now have tanθ = y/x. Similarly, we can obtain the values of the other trigonometric ratios using the right-angled triangle within the unit circle. Also by changing the θ values we can obtain the principal values of these trigonometric ratios.
Unit Circle with Sin Cos and Tan
Any point on the unit circle has coordinates(x, y), which are equal to the trigonometric identities of (cosθ, sinθ). For any values of θ made by the radius line with the positive x-axis, the coordinates of the endpoint of the radius represent the cosine and the sine of the θ values. Here we have cosθ = x, and sinθ = y, and these values are helpful to compute the other trigonometric ratio values. Applying this further we have tanθ = sinθ/cosθ or tanθ = y/x.
Another important point to be understood is that the sinθ and cosθ values always lie between 1 and -1, and the radius value is 1, and it has a value of -1 on the negative x-axis. The entire circle represents a complete angle of 360º and the four quadrant lines of the circle make angles of 90º, 180º, 270º, 360º(0º). At 90º and at 270º the cosθ value is equal to 0 and hence the tan values at these angles are undefined.
Example: Find the value of tan 45º using sin and cos values from the unit circle.
We know that, tan 45° = sin 45°/cos 45°
Using the unit circle chart:
sin 45° = 1/√2
cos 45° = 1/√2
Therefore, tan 45° = sin 45°/cos 45°
= (1/√2)/(1/√2)
= 1
Unit Circle Chart in Radians
The unit circle represents a complete angle of 2π radians. And the unit circle is divided into four quadrants at angles of π/2, π. 3π/2, and 2π respectively. Further within the first quadrant at the angles of 0, π/6, π/4, π/3, π/2 are the standard values, which are applicable to the trigonometric ratios.
The points on the unit circle for these angles represent the standard angle values of the cosine and sine ratios. On close observation of the below figure the values are repeated across the four quadrants, but with a change in sign. This change in sign is because of the reference x-axis and y-axis, which are positive on one side and negative on the other side of the origin. Now with the help of this, we can easily find the trigonometric ratio values of standard angles, across the four quadrants of the unit circle.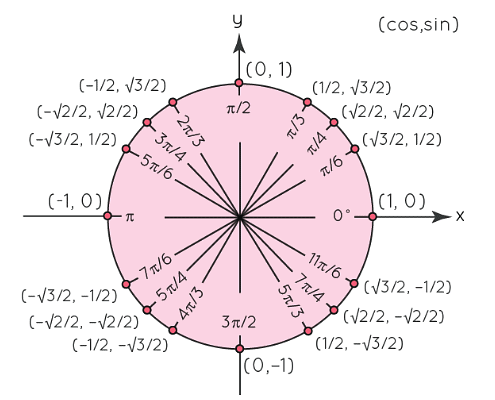
Unit Circle and Trigonometric Identities
The unit circle identities of sine, cosecant, and tangent can be further used to obtain the other trigonometric identities such as cotangent, secant, and cosecant. The unit circle identities such as cosecant, secant, cotangent are the respective reciprocal of the sine, cosine, tangent.
Further, we can obtain the value of tanθ by dividing sinθ with cosθ, and we can obtain the value of cotθ by dividing cosθ with sinθ. For a right triangle placed in a unit circle in the cartesian coordinate plane, with hypotenuse, base, and altitude measuring 1, x, y units respectively, the unit circle identities can be given as,
- sinθ = y/1
- cosθ = x/1
- tanθ = sinθ/cosθ = y/x
- sec(θ = 1/x
- csc(θ) = 1/y
- cot(θ) = cosθ/sinθ = x/y
Unit Circle Pythagorean Identities
The three important Pythagorean identities of trigonometric ratios can be easily understood and proved with the unit circle. The Pythagoras theorem states that in a right-angled triangle the square of the hypotenuse is equal to the sum of the square of the other two sides. The three Pythagorean identities in trigonometry are as follows.
- sin2θ + cos2θ = 1
- 1 + tan2θ = sec2θ
- 1 + cot2θ = cosec2θ
Here we shall try to prove the first identity with the help of the Pythagoras theorem. Let us take x and y as the legs of the right-angled triangle having a hypotenuse 1 unit. Applying Pythagoras theorem we have x2 + y2 = 1 which represents the equation of a unit circle. Also in a unit circle, we have, x = cosθ, and y = sinθ, and applying this in the above statement of the Pythagoras theorem, we have, cos2θ + sin2θ = 1. Thus we have successfully proved the first identity using the Pythagoras theorem. Further within the unit circle, we can also prove the other two Pythagorean identities.
Unit Circle and Trigonometric Values
The various trigonometric identities and their principal angle values can be calculated through the use of a unit circle. In the unit circle, we have cosine as the x-coordinate and sine as the y-coordinate. Let us now find their respective values for θ = 0°, and θ = 90º.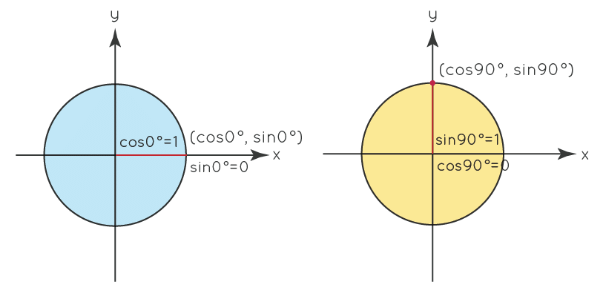
For θ = 0°, the x-coordinate is 1 and the y-coordinate is 0. Therefore, we have cos0º = 1, and sin0º = 0. Let us look at another angle of 90º. Here the value of cos90º = 1, and sin90º = 1. Further, let us use this unit circle and find the important trigonometric function values of θ such as 30º, 45º, 60º. Also, we can also measure these θ values in radians. We know that 360° = 2π radians. We can now convert the angular measures to radian measures and express them in terms of the radians.
Unit Circle Table
The unit circle table is used to list the coordinates of the points on the unit circle that correspond to common angles with the help of trigonometric ratios.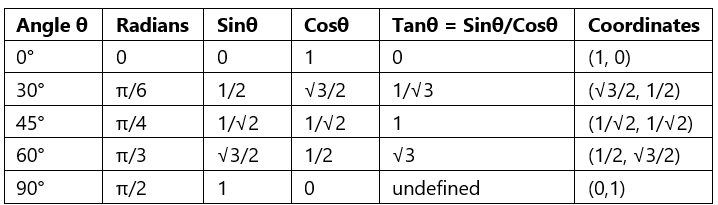
We can find the secant, cosecant, and cotangent functions also using these formulas:
- secθ = 1/cosθ
- cosecθ = 1/sinθ
- cotθ = 1/tanθ
We have discussed the unit circle for the first quadrant. Similarly, we can extend and find the radians for all the unit circle quadrants. The numbers 1/2, 1/√2, √3/2, 0, 1 repeat along with the sign in all 4 quadrants.
Unit Circle in Complex Plane
A unit circle consists of all complex numbers of absolute value as 1. Therefore, it has the equation of |z| = 1. Any complex number z = x + iy will lie on the unit circle with equation given as x2 + y2 = 1.
The unit circle can be considered as unit complex numbers in a complex plane, i.e., the set of complex numbers z given by the form,
z = eit = cos t + i sin t = cis(t)
|
433 videos|220 docs|166 tests
|















